Conectando a Otimização Multiobjetivo Evolutiva
e a Aceleração GPU via Tensorização
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
Com o aumento contínuo da demanda por soluções de otimização complexas em domínios como design de engenharia e gestão de energia, os algoritmos de otimização multiobjetivo evolutiva (EMO) têm atraído ampla atenção devido às suas robustas capacidades na resolução de problemas multiobjetivo. No entanto, à medida que as tarefas de otimização crescem em escala e complexidade, os algoritmos EMO tradicionais baseados em CPU encontram gargalos significativos de desempenho.
Para abordar essa limitação, a equipe EvoX propôs paralelizar algoritmos EMO em GPUs via metodologia de tensorização. Aproveitando esse método, eles projetaram e implementaram com sucesso vários algoritmos EMO acelerados por GPU. Além disso, a equipe desenvolveu o “MoRobtrol”, um conjunto de benchmarks para controle robótico multiobjetivo construído sobre o motor de física Brax, com o objetivo de avaliar sistematicamente o desempenho de algoritmos EMO acelerados por GPU.
Com base nesses avanços de pesquisa, a equipe EvoX lançou o EvoMO, uma biblioteca de algoritmos EMO acelerados por GPU de alto desempenho. O código-fonte correspondente está disponível publicamente no GitHub: https://github.com/EMl-Group/evomo
Metodologia de Tensorização
No campo da otimização computacional, um tensor refere-se a uma estrutura de dados de array multidimensional capaz de representar escalares, vetores, matrizes e dados de ordem superior. Tensorização é o processo de converter estruturas de dados e operações dentro de um algoritmo em forma tensorial, permitindo que o algoritmo aproveite totalmente as capacidades de computação paralela das GPUs.
Em algoritmos EMO, todas as estruturas de dados principais podem ser expressas em formato tensorizado. Os indivíduos em uma população podem ser representados por um tensor de solução X, onde cada vetor linha corresponde a um indivíduo. Os valores da função objetivo formam um tensor de objetivo F. Além disso, estruturas de dados auxiliares como vetores de referência e vetores de peso podem ser expressas como tensores R e W, respectivamente. Essa representação tensorial unificada permite operações em nível de população no nível de representação, estabelecendo uma base sólida para computação paralela em larga escala.
A tensorização das operações de algoritmos EMO é crucial para melhorar a eficiência computacional e pode ser dividida em duas camadas: operações tensoriais básicas e tensorização de fluxo de controle. As operações tensoriais básicas constituem o núcleo da implementação tensorizada de algoritmos EMO, conforme detalhado na Tabela I.
Tabela I: Operações Tensoriais Básicas

A tensorização de fluxo de controle substitui a lógica tradicional de loops e condicionais por operações tensoriais paralelizáveis. Por exemplo, loops for/while podem ser transformados em operações em lote usando mecanismos de broadcasting ou funções de ordem superior como vmap. Da mesma forma, condicionais if-else podem ser substituídos por técnicas de mascaramento, onde condições lógicas são codificadas como tensores booleanos, permitindo alternância flexível entre diferentes caminhos de computação.
Comparada com implementações tradicionais de algoritmos EMO, a abordagem de tensorização oferece vantagens significativas. Primeiro, proporciona maior flexibilidade, lidando naturalmente com dados multidimensionais, enquanto métodos convencionais são frequentemente restritos a operações de matrizes bidimensionais. Segundo, a tensorização melhora significativamente a eficiência computacional através da execução paralela, evitando a sobrecarga associada a loops explícitos e ramificações condicionais. Por fim, simplifica a estrutura do código, resultando em programas mais concisos e fáceis de manter.
Como ilustrado na Fig. 1, por exemplo, a implementação tradicional da verificação de dominância de Pareto depende de loops aninhados para realizar comparações elemento a elemento. Em contraste, a versão tensorizada alcança a mesma funcionalidade através de operações de broadcasting e mascaramento, permitindo avaliação paralela. Isso não apenas reduz a complexidade do código, mas também melhora dramaticamente o desempenho em tempo de execução.

Fig.1: Comparação entre implementações convencional e baseada em tensores da detecção de dominância de Pareto.
De uma perspectiva mais profunda, a tensorização é adequada para aceleração GPU porque as GPUs possuem um grande número de núcleos paralelos, e sua arquitetura de instrução única múltiplas threads (SIMT) se alinha naturalmente com computações tensoriais, particularmente se destacando em operações matriciais. Hardware dedicado como os Tensor Cores da NVIDIA aprimora ainda mais o throughput das operações tensoriais. Em geral, algoritmos que exibem alto paralelismo, contêm tarefas computacionais independentes e têm ramificação condicional mínima são mais adequados para tensorização. Para algoritmos como MOEA/D, que envolvem dependências sequenciais, a estrutura inerente apresenta desafios para a tensorização direta. No entanto, através de refatoração estrutural e desacoplamento de computações críticas, ainda é possível alcançar aceleração paralela eficaz.
Exemplo de Aplicação da Tensorização de Algoritmos
Com base na metodologia de representação tensorizada, a equipe EvoX projetou e implementou versões tensorizadas de três algoritmos EMO clássicos: o NSGA-III baseado em dominância, o MOEA/D baseado em decomposição e o HypE baseado em indicador. A seção a seguir fornece uma explicação detalhada usando o MOEA/D como exemplo. Implementações tensorizadas do NSGA-III e HypE podem ser encontradas no artigo referenciado.
Como ilustrado na Fig. 2, o MOEA/D tradicional decompõe um problema multiobjetivo em múltiplos subproblemas, cada um dos quais é otimizado independentemente. O algoritmo compreende quatro etapas centrais: crossover e mutação, avaliação de fitness, atualização do ponto ideal e atualização de vizinhança. Essas etapas são executadas sequencialmente para cada indivíduo dentro de um único loop. Esse processamento sequencial leva a uma sobrecarga computacional substancial ao lidar com grandes populações, pois cada indivíduo deve completar todas as etapas em ordem, limitando os benefícios potenciais da aceleração GPU. Em particular, a atualização de vizinhança depende de interações entre indivíduos, o que complica ainda mais a paralelização.

Fig.2: Pseudocódigo do MOEA/D
Para abordar a questão das dependências sequenciais no MOEA/D tradicional, a equipe introduziu um método de representação tensorizada dentro do loop interno da seleção ambiental. Ao desacoplar crossover e mutação, avaliação de fitness, atualização do ponto ideal e atualização de vizinhança, esses componentes são tratados como operações independentes. Isso permite o processamento paralelo de todos os indivíduos, levando à construção de um algoritmo MOEA/D tensorizado, referido como TensorMOEA/D. Neste algoritmo, a seleção ambiental é dividida em dois estágios principais: comparação e atualização da população, e seleção de soluções de elite. Esses dois estágios são principalmente tensorizados através de duas aplicações da operação vmap. O processo detalhado é ilustrado na Fig. 3.
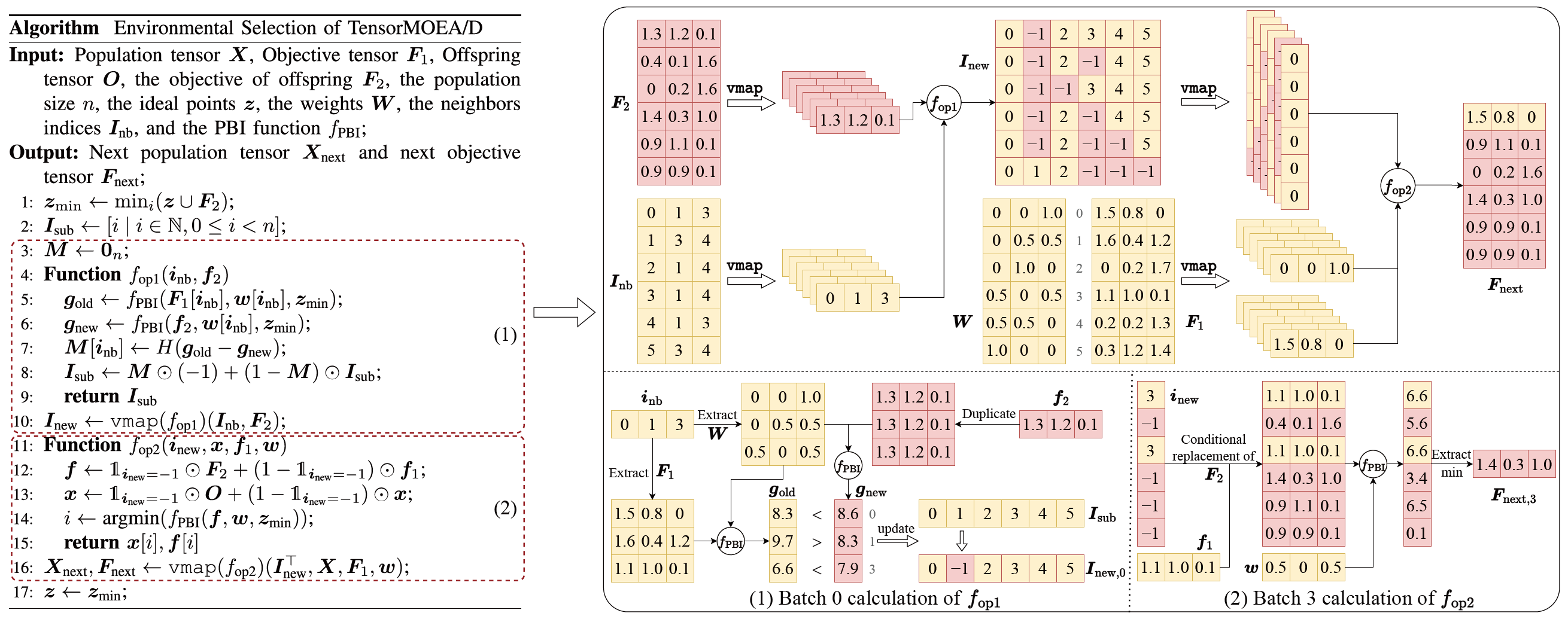
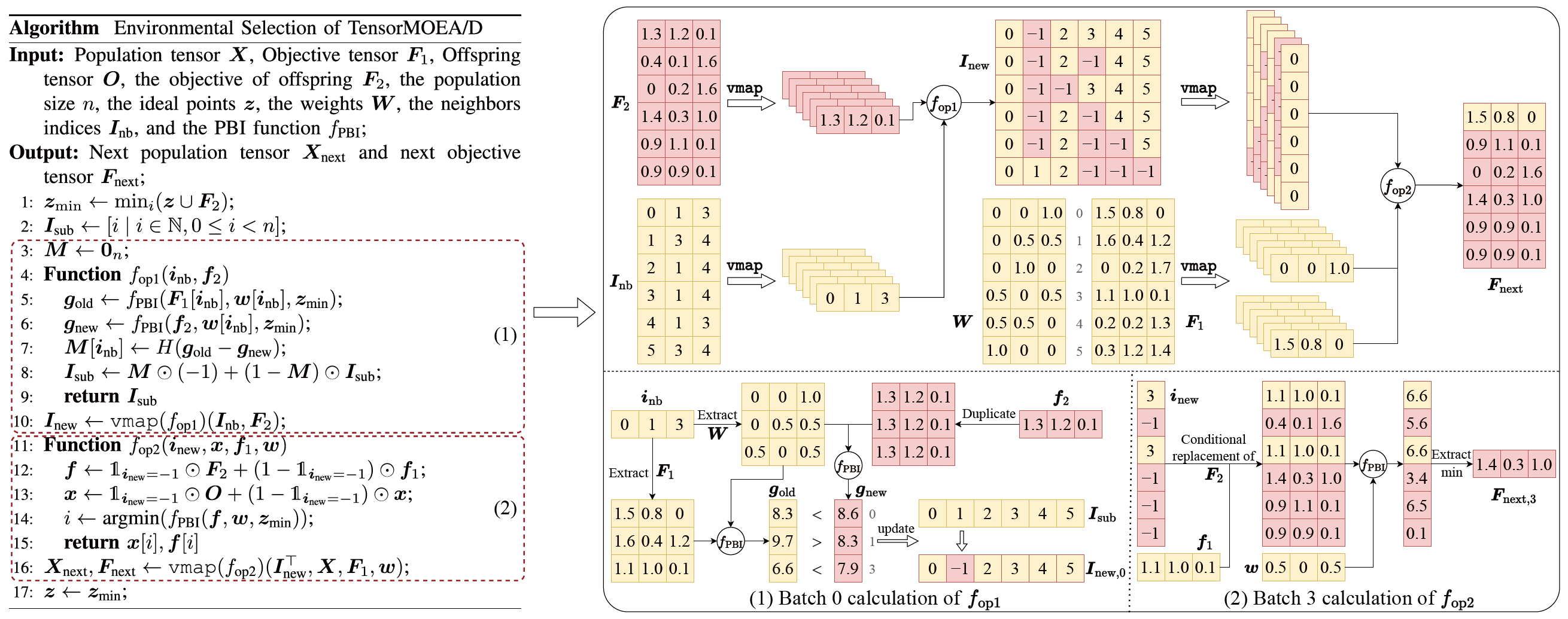
Fig.3: Visão geral da seleção ambiental no algoritmo TensorMOEA/D. Esquerda: Pseudocódigo do algoritmo. Direita: Fluxo de dados tensorial dos módulos (1) e (2). A parte superior da Fig. direita mostra o fluxo de dados tensorial geral para os módulos (1) e (2), enquanto a parte inferior apresenta o fluxo de dados tensorial de cálculo em lote, com o módulo (1) à esquerda e o módulo (2) à direita.
Para obter uma compreensão mais abrangente do valor da tensorização em algoritmos EMO, pode-se resumir a partir de três perspectivas. Primeiro, a tensorização permite uma transformação direta de formulações matemáticas para código eficiente, reduzindo a lacuna entre o design do algoritmo e a implementação. Por exemplo, a Fig. 4 ilustra como o procedimento de ordenação não dominada tensorizado pode ser traduzido diretamente de pseudocódigo para código Python. Segundo, a tensorização simplifica significativamente a estrutura do código ao unificar operações em nível de população em uma única representação tensorial. Isso reduz a dependência de loops e instruções condicionais, melhorando assim a legibilidade e manutenibilidade do código. Terceiro, a tensorização aprimora a reprodutibilidade dos algoritmos. Sua representação estruturada facilita testes comparativos e reprodução consistente de resultados.

Fig.4: A transformação perfeita da ordenação não dominada tensorizada de pseudocódigo (Esquerda) para código Python (Direita).
Demonstração de Desempenho
Para avaliar o desempenho de algoritmos de otimização multiobjetivo acelerados por GPU, a equipe EvoX conduziu sistematicamente três categorias de experimentos, focando em aceleração computacional, desempenho de otimização numérica e eficácia em tarefas de controle robótico multiobjetivo.
Desempenho de Aceleração Computacional:
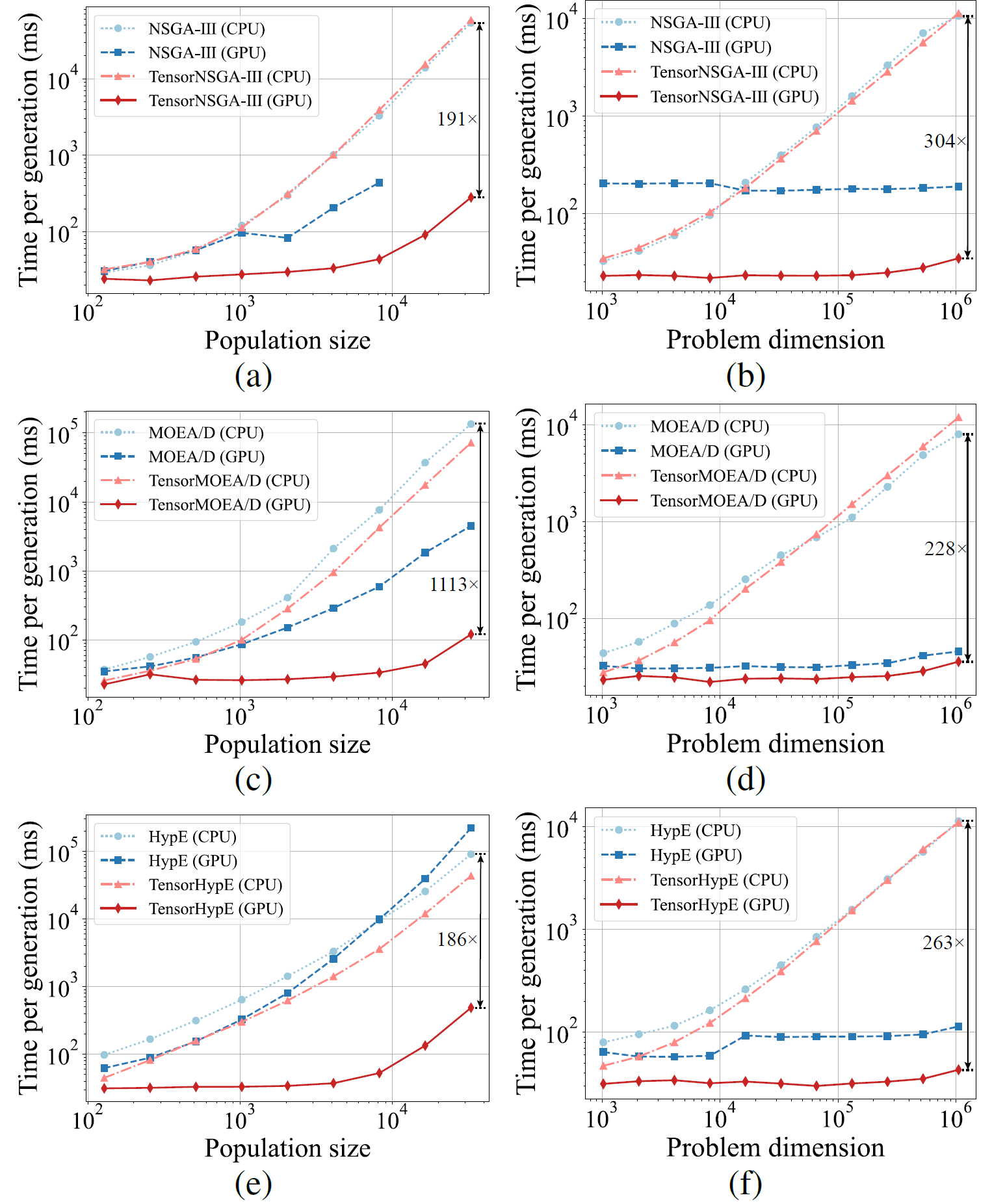
Fig.5: Desempenho comparativo de aceleração de NSGA-III, MOEA/D e HypE com suas contrapartes tensorizadas em plataformas CPU e GPU com tamanhos de população e dimensões de problema variados.
Os resultados experimentais mostram que TensorNSGA-III, TensorMOEA/D e TensorHypE alcançam velocidades de execução significativamente maiores em GPUs comparadas às suas contrapartes não tensorizadas baseadas em CPU. À medida que o tamanho da população e a dimensionalidade do problema aumentam, a aceleração máxima observada chega a 1113x. Os algoritmos tensorizados demonstram excelente escalabilidade e estabilidade ao lidar com tarefas computacionais de larga escala — seu tempo de execução aumenta apenas marginalmente, mantendo desempenho consistentemente alto. Esses resultados destacam as vantagens substanciais da tensorização para aceleração GPU em otimização multiobjetivo.
Desempenho no Conjunto de Testes LSMOP:
Tabela II: Resultados Estatísticos (Média e Desvio Padrão) do IGD e Tempo de Execução (s) para Algoritmos EMO Não Tensorizados e Tensorizados em LSMOP1—LSMOP9. Todos os Experimentos São em uma GPU RTX 4090 e os Melhores Resultados Estão Destacados.
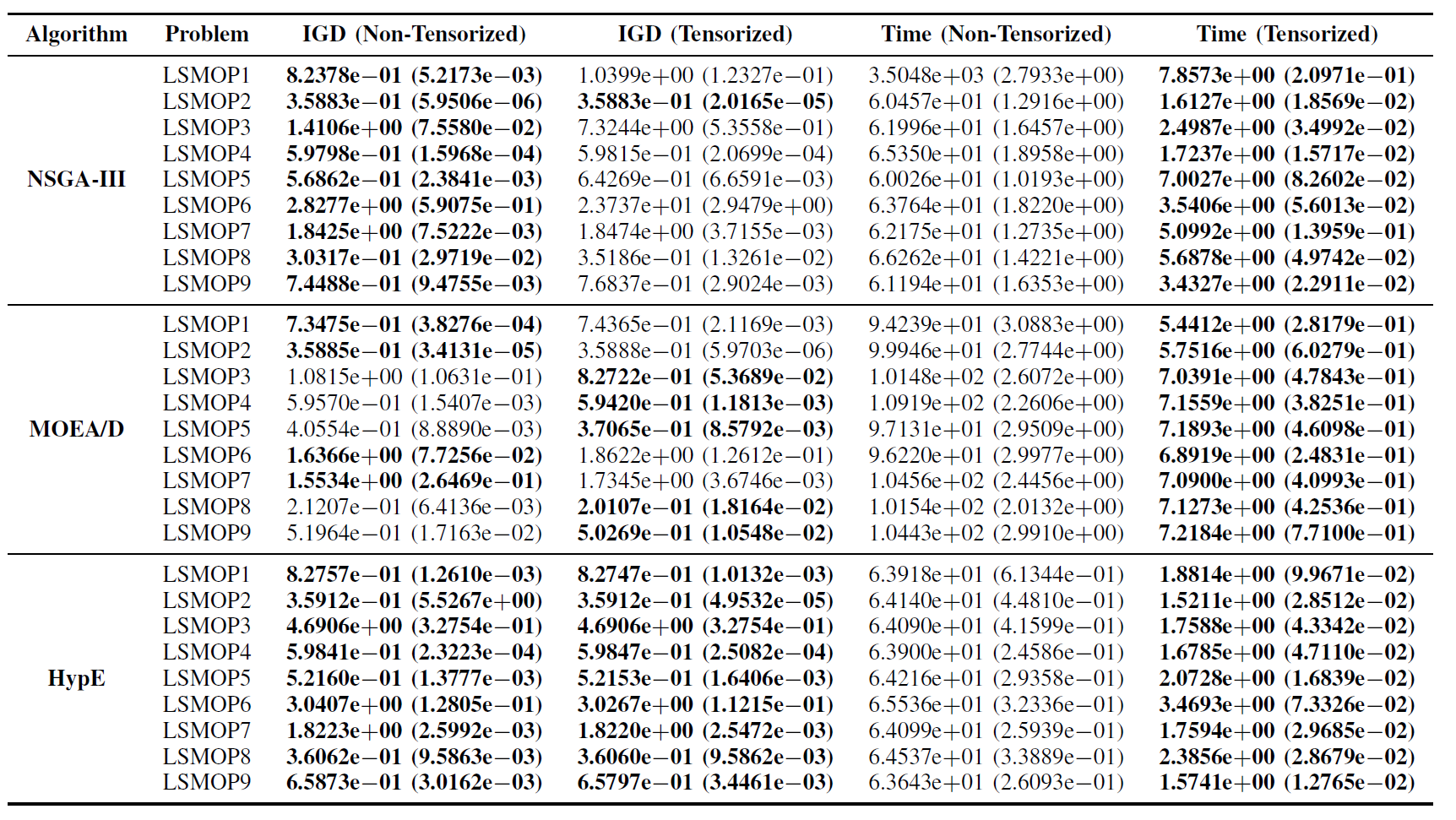
Os resultados experimentais indicam que os algoritmos EMO acelerados por GPU baseados em representações tensorizadas melhoram significativamente a eficiência computacional enquanto mantêm, e em alguns casos até superam, a precisão de otimização de suas contrapartes originais.
Tarefas de Controle Robótico Multiobjetivo:
Para avaliar de forma abrangente o desempenho prático de algoritmos EMO acelerados por GPU, a equipe desenvolveu um conjunto de benchmarks chamado MoRobtrol para controle robótico multiobjetivo. As tarefas incluídas neste conjunto estão listadas na Tabela III.
Tabela III: Visão Geral dos Problemas de Controle Robótico Multiobjetivo no Conjunto de Benchmarks MoRobtrol Proposto
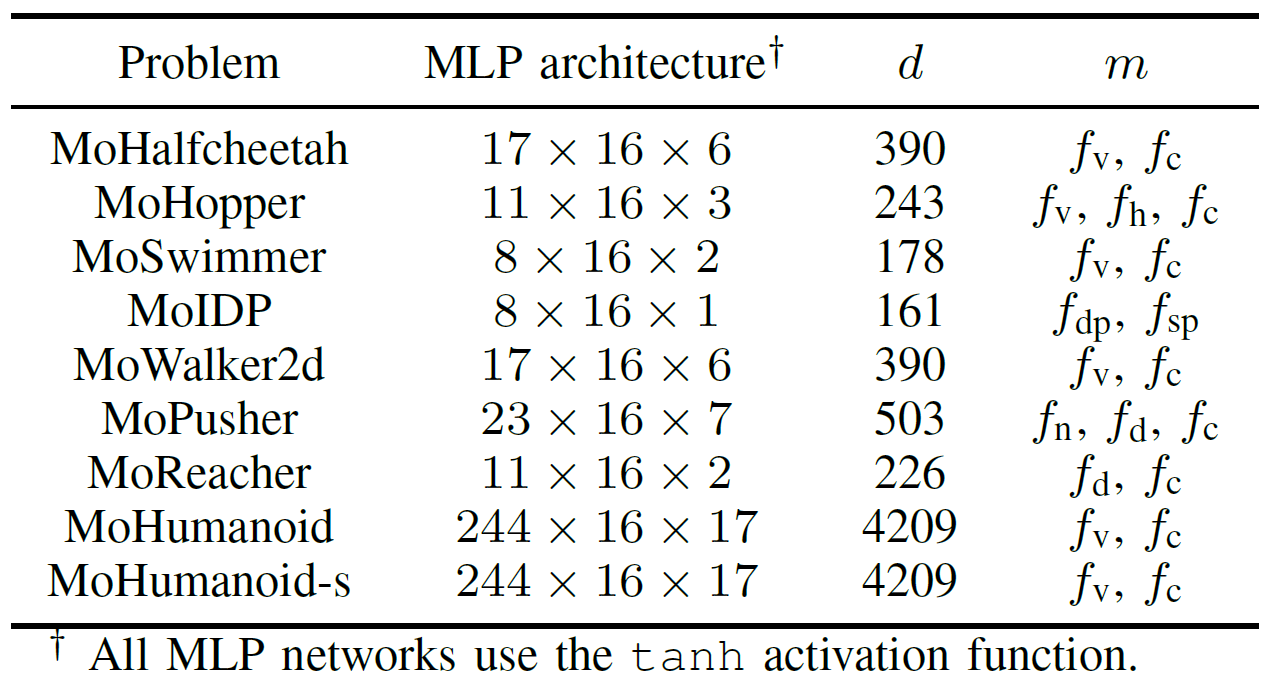
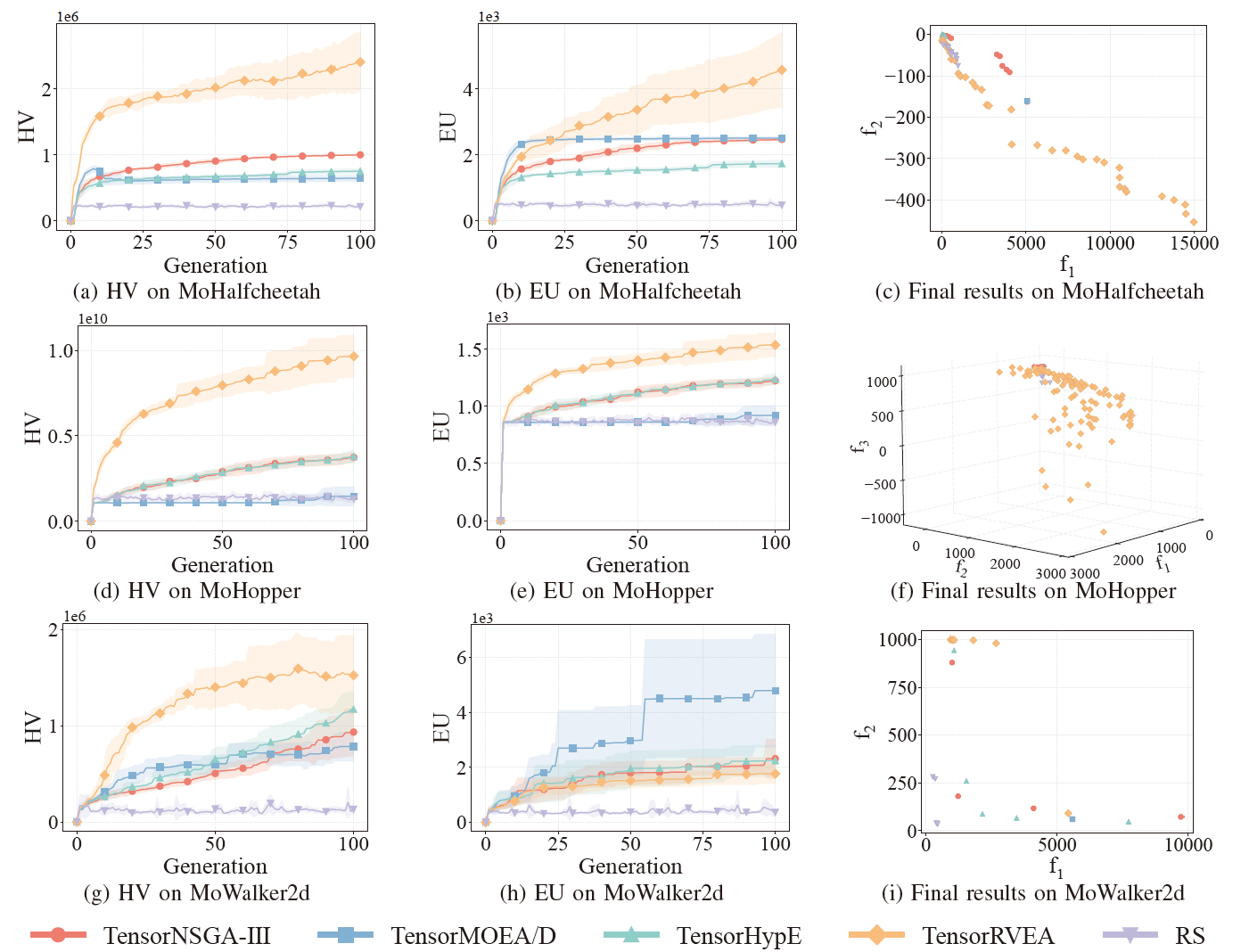
Fig.6: Desempenho comparativo (HV, EU e visualização dos resultados finais) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e busca aleatória (RS) em problemas variados: MoHalfcheetah (390D), MoHopper (243D) e MoWalker2d (390D). Nota: Valores mais altos para todas as métricas indicam melhor desempenho.
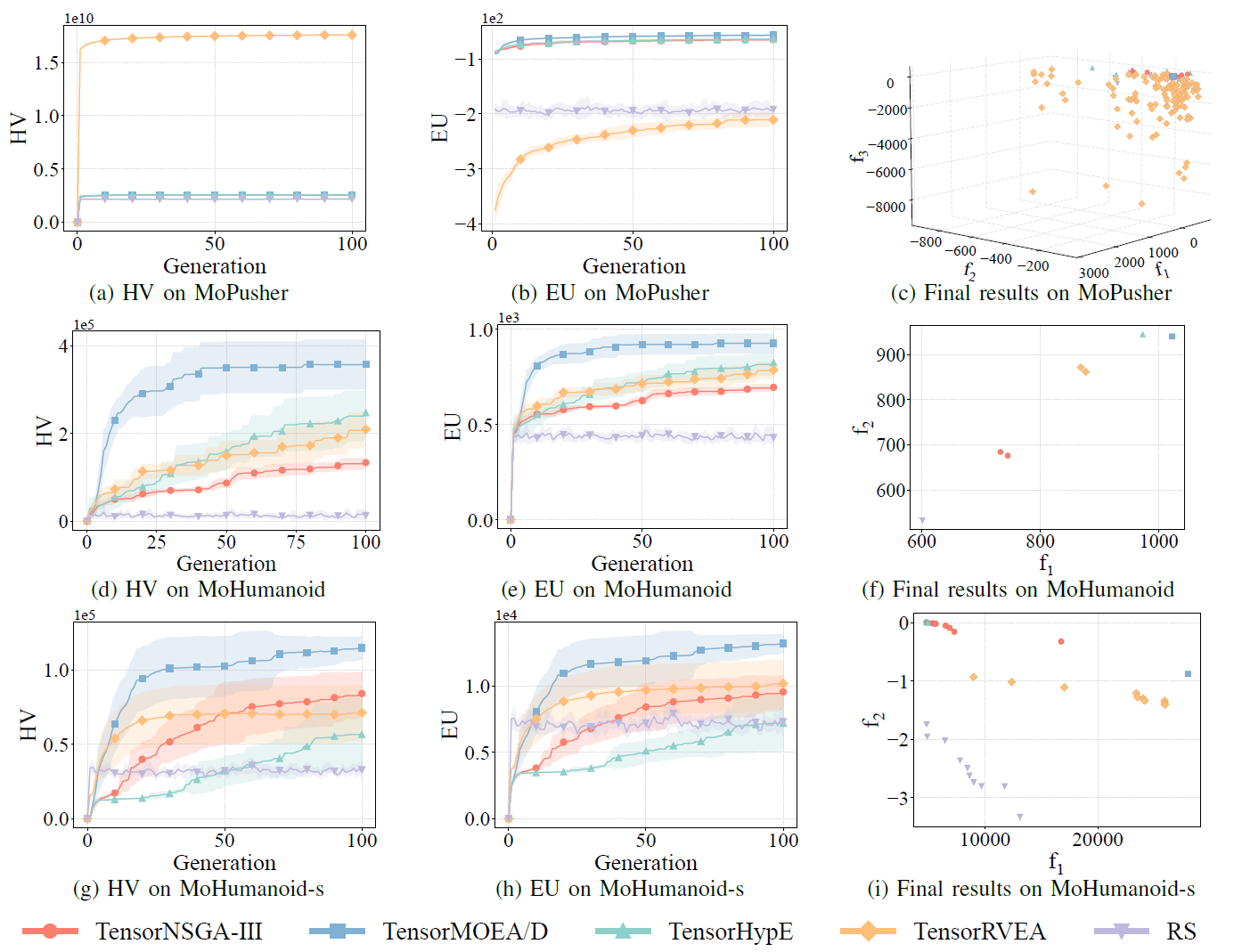
Fig.7: Desempenho comparativo (HV, EU e visualização dos resultados finais) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e busca aleatória (RS) em problemas variados: MoPusher (503D), MoHumanoid (4209D) e MoHumanoid-s (4209D). Nota: Valores mais altos para todas as métricas indicam melhor desempenho.
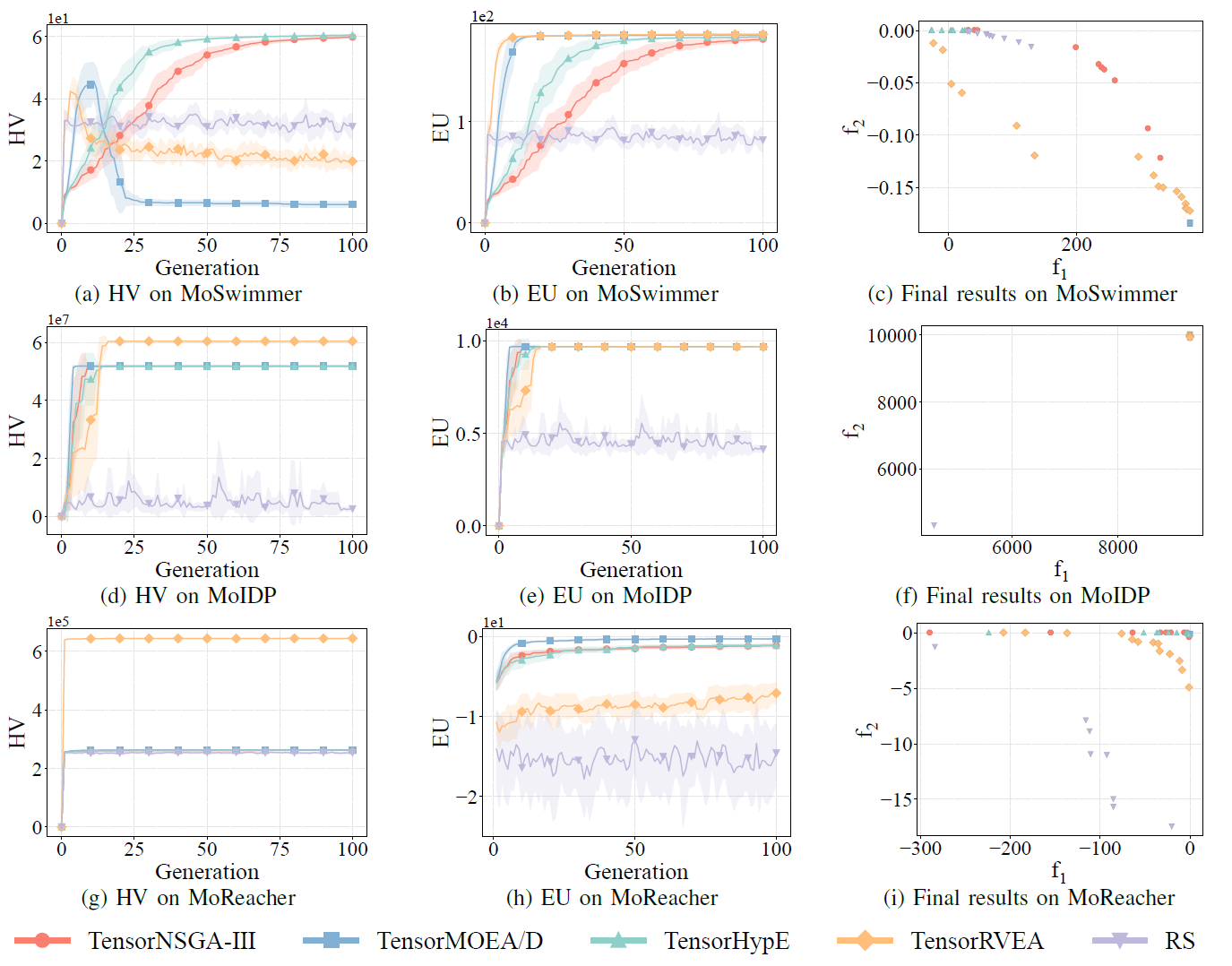
Fig.8: Desempenho comparativo (HV, EU e visualização dos resultados finais) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e busca aleatória (RS) em problemas variados: MoSwimmer (178D), MoIDP (161D) e MoReacher (226D). Nota: Valores mais altos para todas as métricas indicam melhor desempenho.
Os experimentos compararam o desempenho de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e Busca Aleatória (RS) dentro do benchmark MoRobtrol. Os resultados mostram que o TensorRVEA alcançou o melhor desempenho geral, obtendo os maiores valores de HV e demonstrando boa diversidade de soluções em múltiplos ambientes. O TensorMOEA/D exibiu forte adaptabilidade em tarefas de larga escala, particularmente se destacando na consistência de preferência das soluções. TensorNSGA-III e TensorHypE mostraram desempenho similar e foram competitivos em várias tarefas. No geral, algoritmos tensorizados baseados em decomposição demonstraram vantagens superiores na resolução de problemas de larga escala e complexos.
Conclusão e Trabalhos Futuros Este estudo propõe uma metodologia de representação tensorizada para abordar as limitações dos algoritmos EMO tradicionais baseados em CPU em termos de eficiência computacional e escalabilidade. A abordagem foi aplicada a vários algoritmos representativos, incluindo NSGA-III, MOEA/D e HypE, alcançando melhorias significativas de desempenho em GPUs enquanto mantém a qualidade das soluções. Para validar sua aplicabilidade prática, a equipe também desenvolveu o MoRobtrol, um conjunto de benchmarks de controle robótico multiobjetivo que reformula tarefas de controle robótico em ambientes de simulação física como problemas de otimização multiobjetivo. Os resultados demonstram o potencial de algoritmos tensorizados em cenários computacionalmente intensivos como inteligência incorporada. Embora o método de tensorização tenha melhorado substancialmente a eficiência algorítmica, ainda há espaço para aprimoramentos adicionais. Direções futuras incluem melhorar operadores centrais como ordenação não dominada, projetar novas operações tensorizadas para sistemas multi-GPU e integrar dados em larga escala e técnicas de deep learning para aprimorar ainda mais o desempenho em problemas de otimização de larga escala.
Código Open Source / Recursos da Comunidade
Artigo:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
Projeto Upstream (EvoX):
https://github.com/EMI-Group/evox
Grupo QQ: 297969717

O EvoMO é construído sobre o framework EvoX. Se você tem interesse em saber mais sobre o EvoX, confira o artigo oficial sobre o EvoX 1.0 publicado em nossa conta pública do WeChat para mais detalhes.


