Relier l’optimisation multi-objectif évolutionnaire
et l’accélération GPU via la tensorisation
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
Avec la demande croissante de solutions d’optimisation complexes dans des domaines tels que la conception d’ingénierie et la gestion de l’énergie, les algorithmes d’optimisation multi-objectif évolutionnaire (EMO) ont suscité une attention considérable en raison de leurs capacités robustes dans la résolution de problèmes multi-objectifs. Cependant, à mesure que les tâches d’optimisation gagnent en échelle et en complexité, les algorithmes EMO traditionnels basés sur CPU rencontrent des goulots d’étranglement significatifs en termes de performances.
Pour remédier à cette limitation, l’équipe EvoX a proposé de paralléliser les algorithmes EMO sur GPU via la méthodologie de tensorisation. En exploitant cette méthode, ils ont conçu et implémenté avec succès plusieurs algorithmes EMO accélérés par GPU. De plus, l’équipe a développé “MoRobtrol”, une suite de benchmarks pour le contrôle robotique multi-objectif construite sur le moteur physique Brax, visant à évaluer systématiquement les performances des algorithmes EMO accélérés par GPU.
Sur la base de ces avancées de recherche, l’équipe EvoX a publié EvoMO, une bibliothèque d’algorithmes EMO haute performance accélérée par GPU. Le code source correspondant est disponible publiquement sur GitHub : https://github.com/EMl-Group/evomo
Méthodologie de tensorisation
Dans le domaine de l’optimisation computationnelle, un tenseur désigne une structure de données sous forme de tableau multidimensionnel capable de représenter des scalaires, des vecteurs, des matrices et des données d’ordre supérieur. La tensorisation est le processus de conversion des structures de données et des opérations d’un algorithme sous forme tensorielle, permettant à l’algorithme d’exploiter pleinement les capacités de calcul parallèle des GPU.
Dans les algorithmes EMO, toutes les structures de données clés peuvent être exprimées sous un format tensorisé. Les individus d’une population peuvent être représentés par un tenseur de solutions X, où chaque vecteur ligne correspond à un individu. Les valeurs de la fonction objectif forment un tenseur objectif F. De plus, les structures de données auxiliaires telles que les vecteurs de référence et les vecteurs de poids peuvent être exprimées sous forme de tenseurs R et W, respectivement. Cette représentation tensorielle unifiée permet des opérations au niveau de la population sur le plan de la représentation, posant une base solide pour le calcul parallèle à grande échelle.
La tensorisation des opérations des algorithmes EMO est cruciale pour améliorer l’efficacité computationnelle et peut être divisée en deux couches : les opérations tensorielles de base et la tensorisation du flux de contrôle. Les opérations tensorielles de base constituent le coeur de l’implémentation tensorisée des algorithmes EMO, comme détaillé dans le Tableau I.
Tableau I : Opérations tensorielles de base

La tensorisation du flux de contrôle remplace la logique traditionnelle de boucles et de conditions par des opérations tensorielles parallélisables. Par exemple, les boucles for/while peuvent être transformées en opérations par lots en utilisant des mécanismes de diffusion (broadcasting) ou des fonctions d’ordre supérieur telles que vmap. De même, les conditions if-else peuvent être remplacées par des techniques de masquage, où les conditions logiques sont encodées sous forme de tenseurs booléens, permettant une commutation flexible entre différents chemins de calcul.
Comparée aux implémentations traditionnelles d’algorithmes EMO, l’approche de tensorisation offre des avantages significatifs. Premièrement, elle offre une plus grande flexibilité, gérant naturellement les données multidimensionnelles, alors que les méthodes conventionnelles sont souvent limitées aux opérations matricielles bidimensionnelles. Deuxièmement, la tensorisation améliore significativement l’efficacité computationnelle grâce à l’exécution parallèle, évitant la surcharge associée aux boucles explicites et aux branches conditionnelles. Enfin, elle simplifie la structure du code, résultant en des programmes plus concis et maintenables.
Comme illustré dans la Fig. 1, par exemple, l’implémentation traditionnelle de la vérification de dominance de Pareto repose sur des boucles imbriquées pour effectuer des comparaisons élément par élément. En revanche, la version tensorisée réalise la même fonctionnalité grâce à des opérations de diffusion et de masquage, permettant une évaluation parallèle. Cela réduit non seulement la complexité du code, mais améliore aussi considérablement les performances d’exécution.

Fig.1 : Comparaison entre les implémentations conventionnelle et tensorisée de la détection de dominance de Pareto.
D’un point de vue plus approfondi, la tensorisation est bien adaptée à l’accélération GPU car les GPU possèdent un grand nombre de coeurs parallèles, et leur architecture SIMT (single-instruction multiple-thread) s’aligne naturellement avec les calculs tensoriels, excellant particulièrement dans les opérations matricielles. Du matériel dédié tel que les Tensor Cores de NVIDIA améliore encore le débit des opérations tensorielles. En général, les algorithmes qui présentent un haut parallélisme, contiennent des tâches de calcul indépendantes et ont un minimum de branchements conditionnels sont plus propices à la tensorisation. Pour des algorithmes comme MOEA/D, qui impliquent des dépendances séquentielles, la structure inhérente pose des défis à la tensorisation directe. Cependant, grâce à la refactorisation structurelle et au découplage des calculs critiques, il est toujours possible d’atteindre une accélération parallèle efficace.
Exemple d’application de la tensorisation d’algorithmes
Sur la base de la méthodologie de représentation tensorisée, l’équipe EvoX a conçu et implémenté des versions tensorisées de trois algorithmes EMO classiques : NSGA-III basé sur la dominance, MOEA/D basé sur la décomposition, et HypE basé sur les indicateurs. La section suivante fournit une explication détaillée en utilisant MOEA/D comme exemple. Les implémentations tensorisées de NSGA-III et HypE peuvent être trouvées dans l’article de référence.
Comme illustré dans la Fig. 2, le MOEA/D traditionnel décompose un problème multi-objectif en plusieurs sous-problèmes, chacun étant optimisé indépendamment. L’algorithme comprend quatre étapes fondamentales : croisement et mutation, évaluation de la fitness, mise à jour du point idéal et mise à jour du voisinage. Ces étapes sont exécutées séquentiellement pour chaque individu dans une seule boucle. Ce traitement séquentiel entraîne une surcharge computationnelle substantielle lors du traitement de grandes populations, car chaque individu doit compléter toutes les étapes dans l’ordre, limitant les bénéfices potentiels de l’accélération GPU. En particulier, la mise à jour du voisinage repose sur les interactions entre individus, ce qui complique davantage la parallélisation.

Fig.2 : Pseudocode de MOEA/D
Pour résoudre le problème des dépendances séquentielles dans le MOEA/D traditionnel, l’équipe a introduit une méthode de représentation tensorisée au sein de la boucle interne de la sélection environnementale. En découplant le croisement et la mutation, l’évaluation de la fitness, la mise à jour du point idéal et la mise à jour du voisinage, ces composants sont traités comme des opérations indépendantes. Cela permet le traitement parallèle de tous les individus, conduisant à la construction d’un algorithme MOEA/D tensorisé, appelé TensorMOEA/D. Dans cet algorithme, la sélection environnementale est divisée en deux étapes principales : comparaison et mise à jour de la population, et sélection des solutions élites. Ces deux étapes sont principalement tensorisées grâce à deux applications de l’opération vmap. Le processus détaillé est illustré dans la Fig. 3.
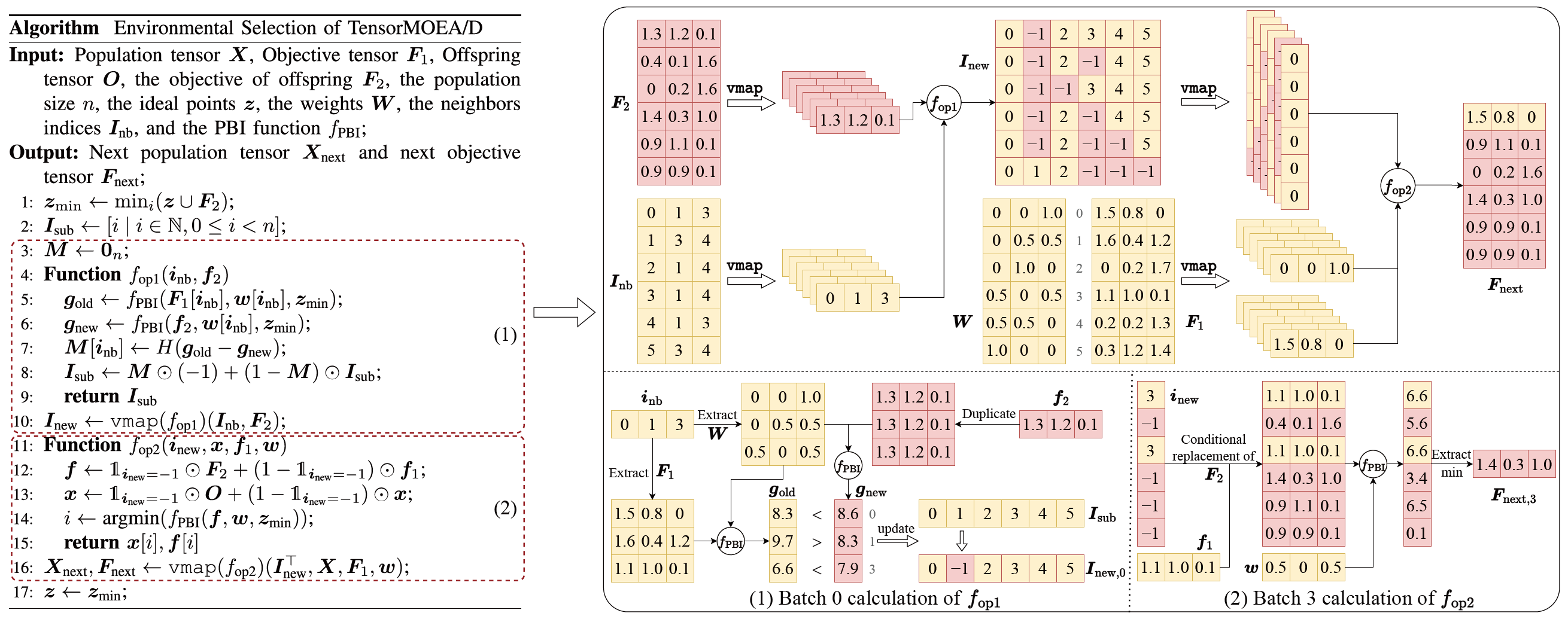
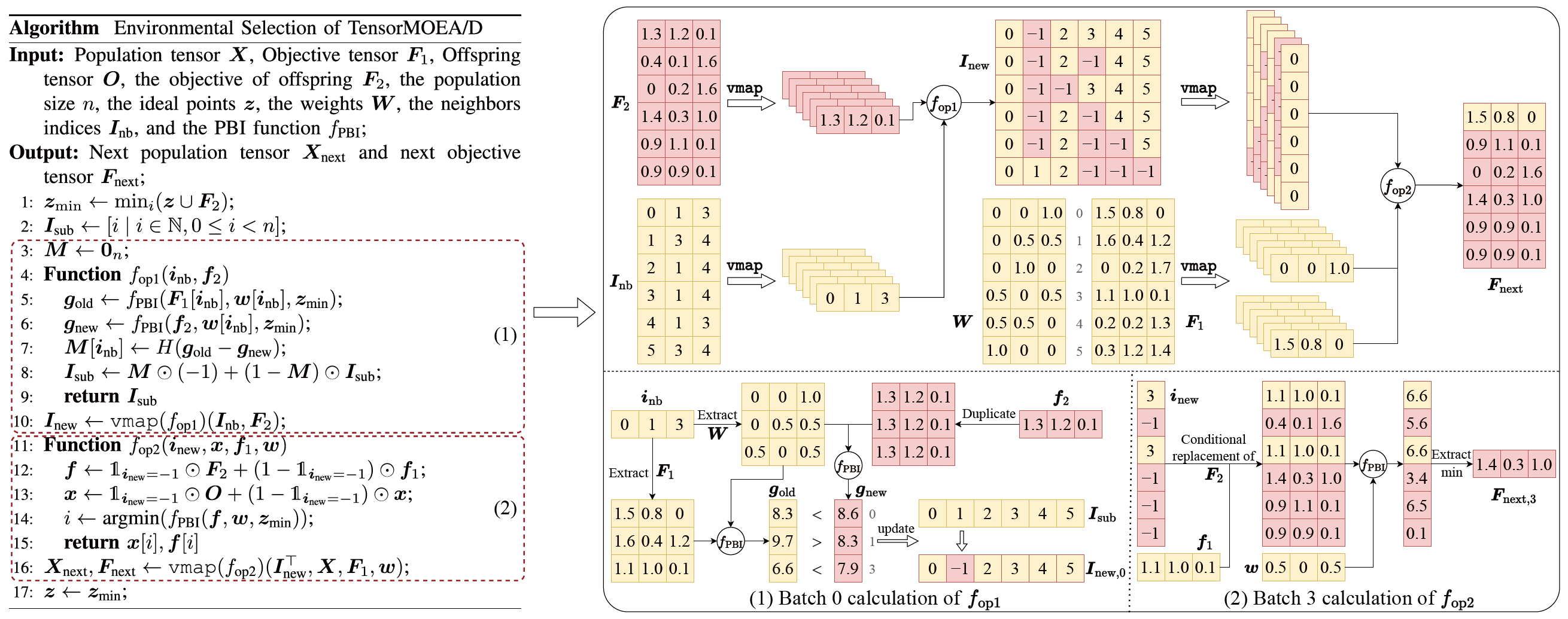
Fig.3 : Vue d’ensemble de la sélection environnementale dans l’algorithme TensorMOEA/D. Gauche : Pseudocode de l’algorithme. Droite : Flux de données tensoriel des modules (1) et (2). La partie supérieure de la figure de droite montre le flux de données tensoriel global pour les modules (1) et (2), tandis que la partie inférieure présente le flux de données tensoriel du calcul par lots, avec le module (1) à gauche et le module (2) à droite.
Pour mieux comprendre la valeur de la tensorisation dans les algorithmes EMO, on peut la résumer selon trois perspectives. Premièrement, la tensorisation permet une transformation directe des formulations mathématiques en code efficace, réduisant l’écart entre la conception d’algorithmes et leur implémentation. Par exemple, la Fig. 4 illustre comment la procédure de tri non dominé tensorisée peut être traduite directement du pseudocode en code Python. Deuxièmement, la tensorisation simplifie significativement la structure du code en unifiant les opérations au niveau de la population en une seule représentation tensorielle. Cela réduit la dépendance aux boucles et aux instructions conditionnelles, améliorant ainsi la lisibilité et la maintenabilité du code. Troisièmement, la tensorisation améliore la reproductibilité des algorithmes. Sa représentation structurée facilite les tests comparatifs et la reproduction cohérente des résultats.

Fig.4 : La transformation transparente du tri non dominé tensorisé du pseudocode (gauche) au code Python (droite).
Démonstration des performances
Pour évaluer les performances des algorithmes d’optimisation multi-objectif accélérés par GPU, l’équipe EvoX a systématiquement mené trois catégories d’expériences, portant sur l’accélération computationnelle, les performances d’optimisation numérique et l’efficacité dans les tâches de contrôle robotique multi-objectif.
Performances d’accélération computationnelle :
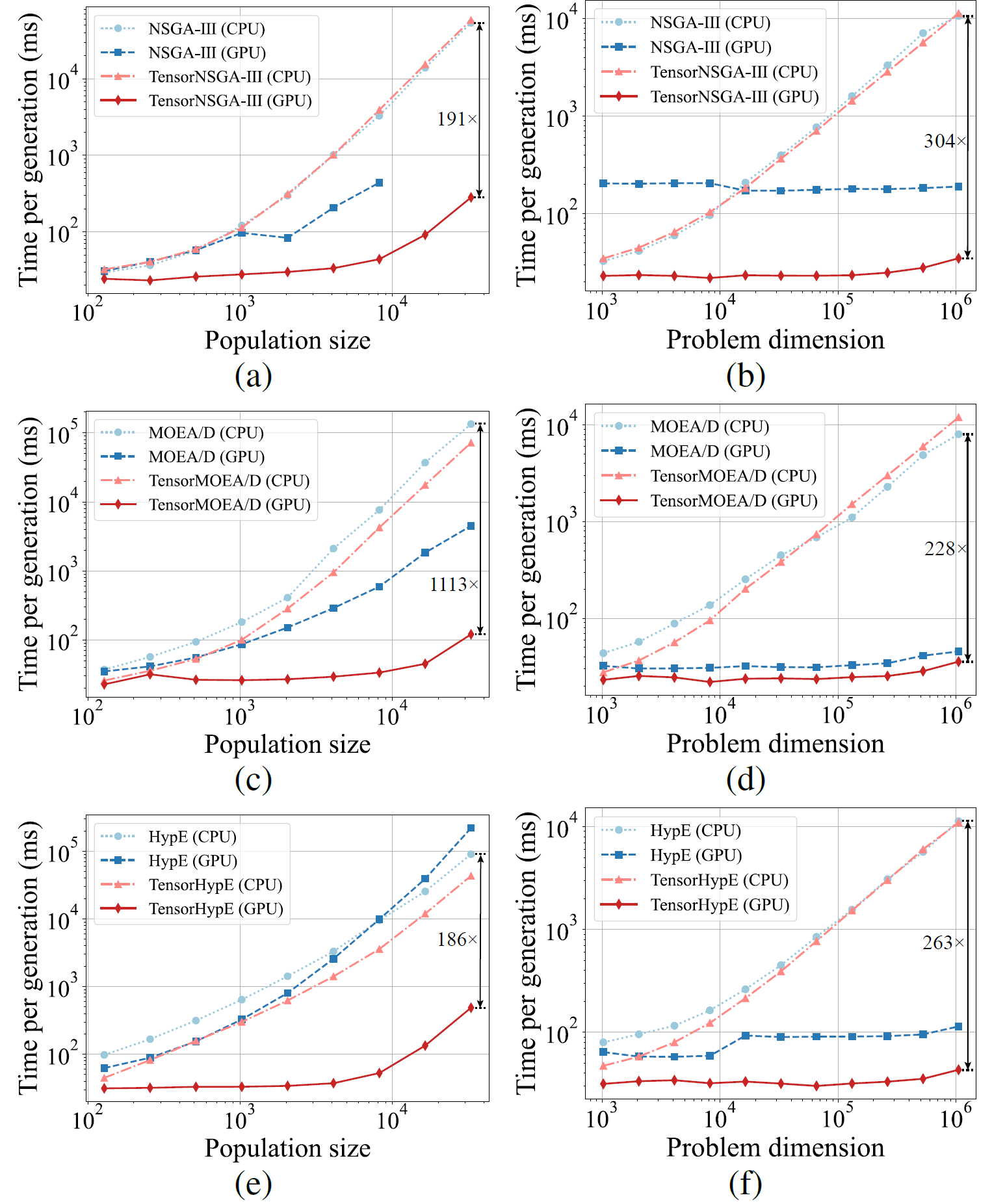
Fig.5 : Performances comparatives d’accélération de NSGA-III, MOEA/D et HypE avec leurs homologues tensorisés sur les plateformes CPU et GPU pour différentes tailles de population et dimensions de problème.
Les résultats expérimentaux montrent que TensorNSGA-III, TensorMOEA/D et TensorHypE atteignent des vitesses d’exécution significativement plus élevées sur GPU par rapport à leurs homologues non tensorisés sur CPU. À mesure que la taille de la population et la dimensionnalité du problème augmentent, l’accélération maximale observée atteint jusqu’à 1113x. Les algorithmes tensorisés démontrent une excellente évolutivité et stabilité lors du traitement de tâches computationnelles à grande échelle — leur temps d’exécution n’augmente que marginalement, tout en maintenant des performances constamment élevées. Ces résultats soulignent les avantages substantiels de la tensorisation pour l’accélération GPU dans l’optimisation multi-objectif.
Performances sur la suite de tests LSMOP :
Tableau II : Résultats statistiques (moyenne et écart-type) de l’IGD et du temps d’exécution (s) pour les algorithmes EMO non tensorisés et tensorisés sur LSMOP1—LSMOP9. Toutes les expériences sont réalisées sur un GPU RTX 4090 et les meilleurs résultats sont mis en évidence.
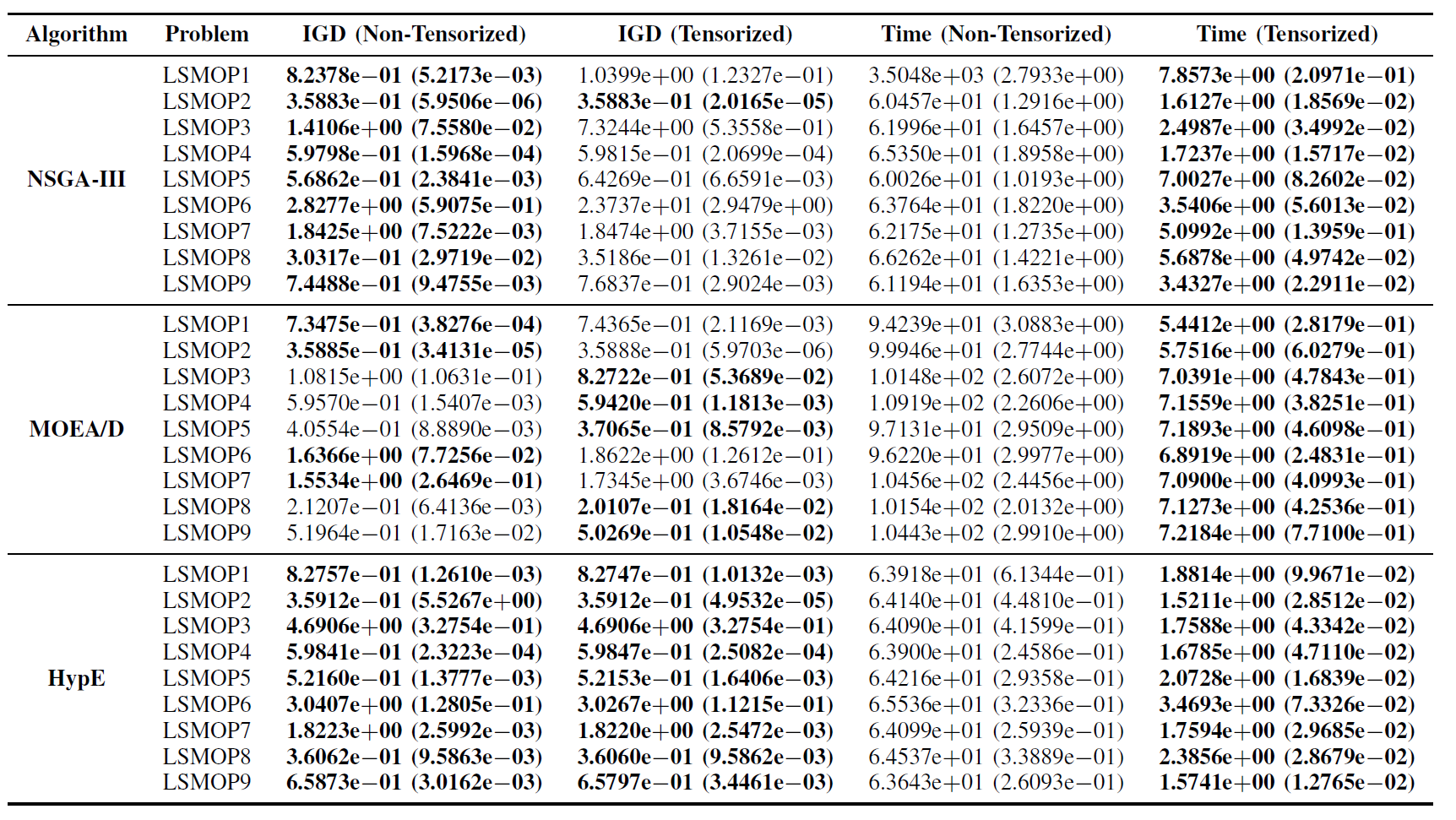
Les résultats expérimentaux indiquent que les algorithmes EMO accélérés par GPU basés sur des représentations tensorisées améliorent significativement l’efficacité computationnelle tout en maintenant, et dans certains cas en surpassant, la précision d’optimisation de leurs homologues originaux.
Tâches de contrôle robotique multi-objectif :
Pour évaluer de manière exhaustive les performances pratiques des algorithmes EMO accélérés par GPU, l’équipe a développé une suite de benchmarks nommée MoRobtrol pour le contrôle robotique multi-objectif. Les tâches incluses dans cette suite sont listées dans le Tableau III.
Tableau III : Vue d’ensemble des problèmes de contrôle robotique multi-objectif dans la suite de benchmarks MoRobtrol proposée
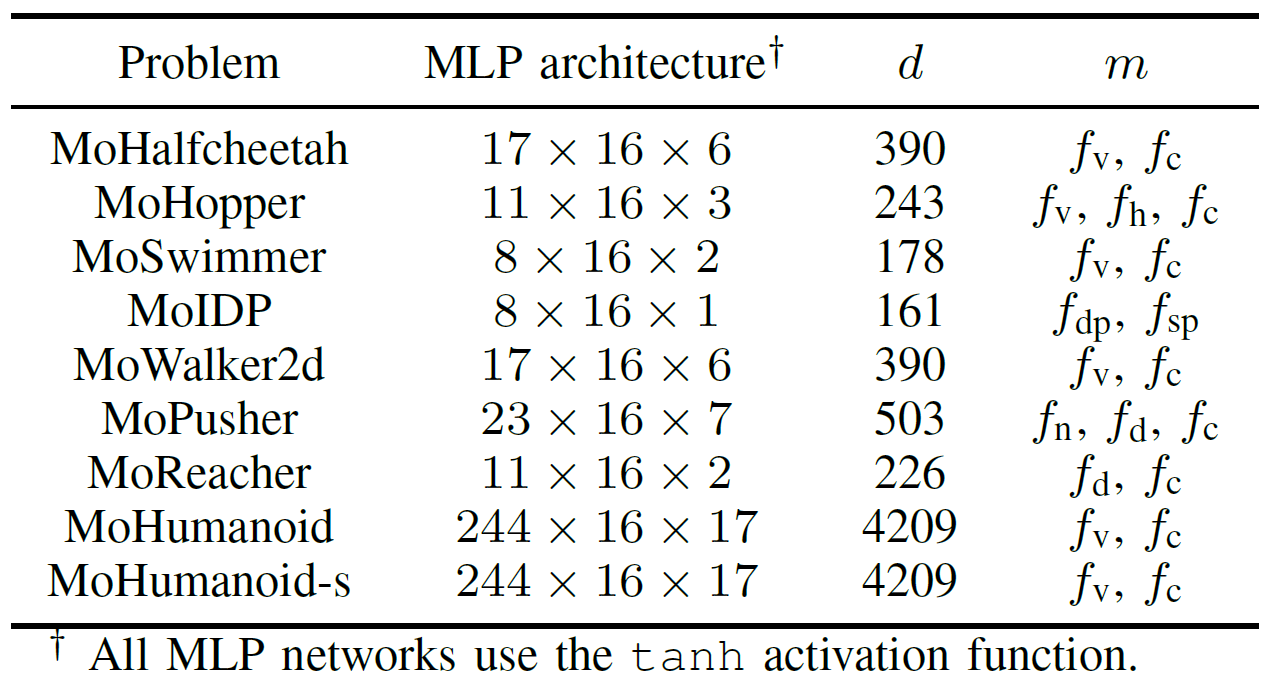
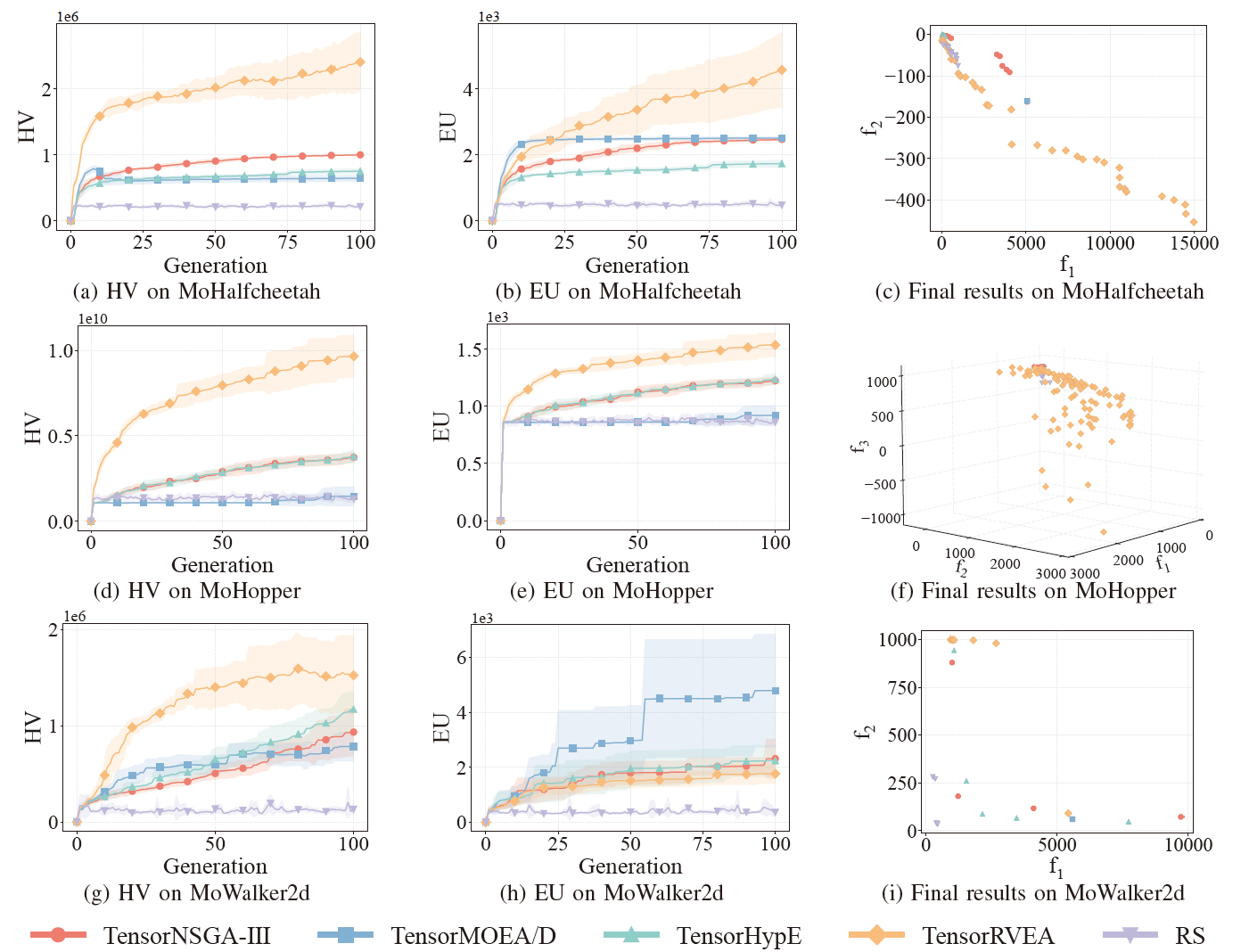
Fig.6 : Performances comparatives (HV, EU et visualisation des résultats finaux) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA et de la recherche aléatoire (RS) sur différents problèmes : MoHalfcheetah (390D), MoHopper (243D) et MoWalker2d (390D). Note : Des valeurs plus élevées pour toutes les métriques indiquent de meilleures performances.
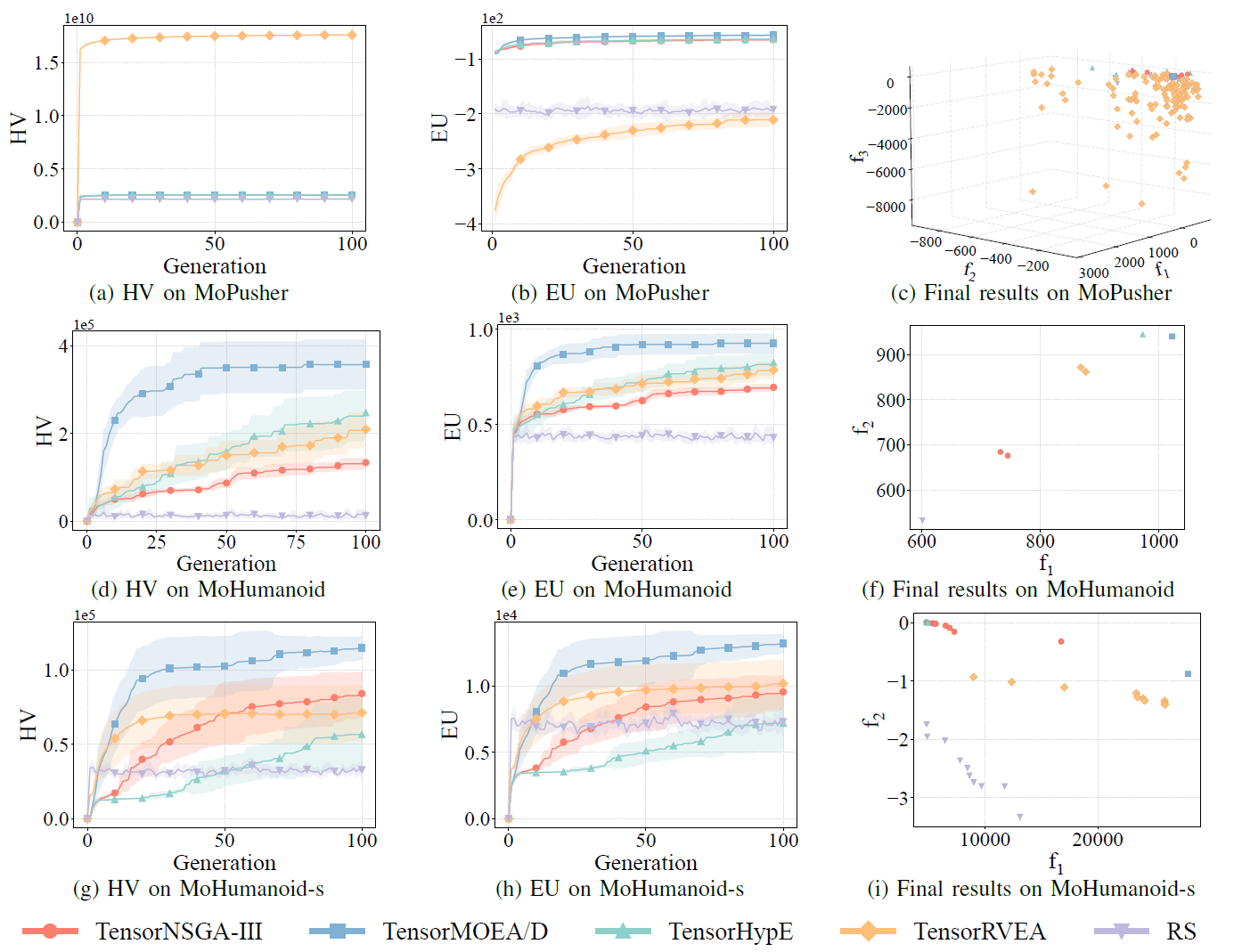
Fig.7 : Performances comparatives (HV, EU et visualisation des résultats finaux) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA et de la recherche aléatoire (RS) sur différents problèmes : MoPusher (503D), MoHumanoid (4209D) et MoHumanoid-s (4209D). Note : Des valeurs plus élevées pour toutes les métriques indiquent de meilleures performances.
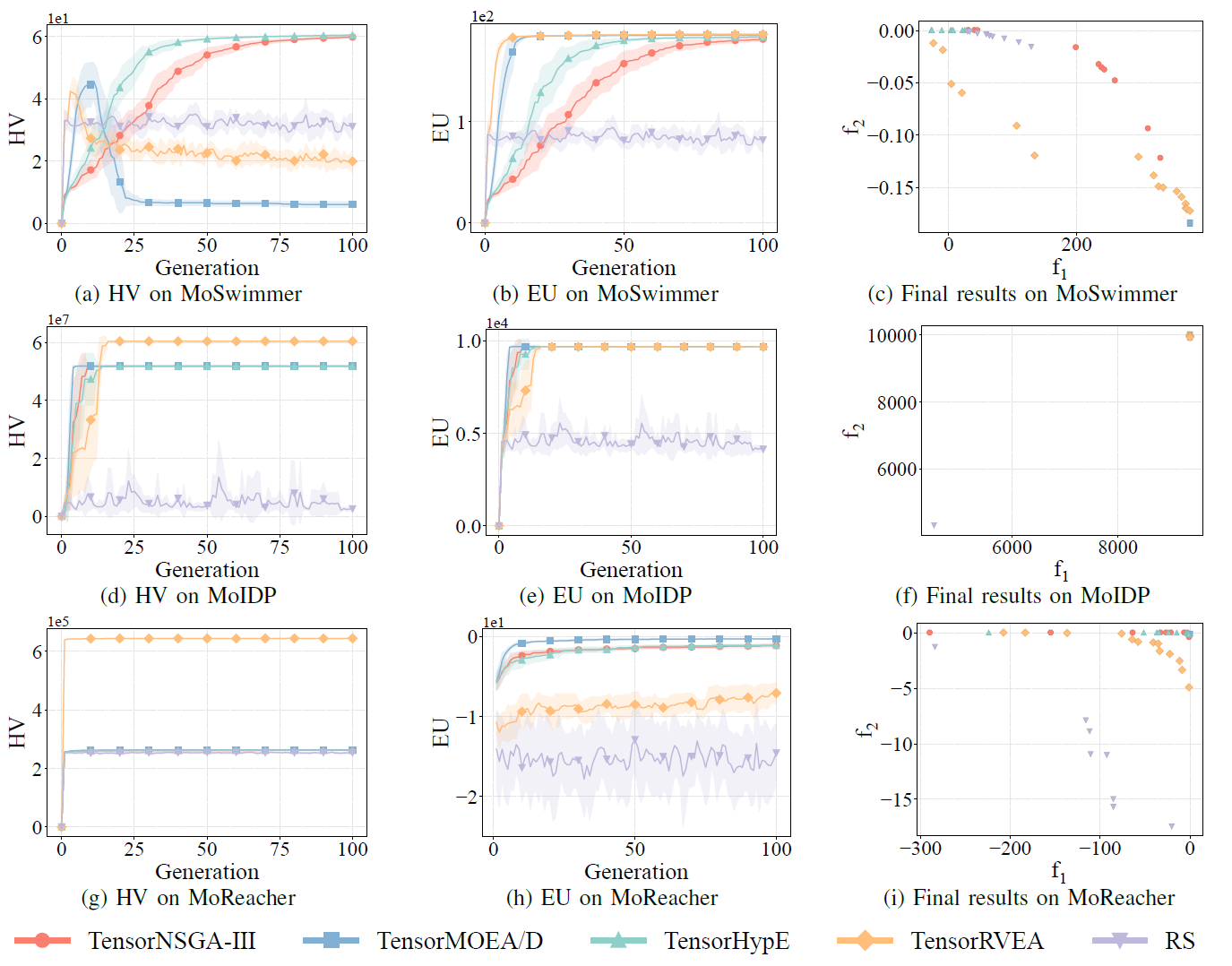
Fig.8 : Performances comparatives (HV, EU et visualisation des résultats finaux) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA et de la recherche aléatoire (RS) sur différents problèmes : MoSwimmer (178D), MoIDP (161D) et MoReacher (226D). Note : Des valeurs plus élevées pour toutes les métriques indiquent de meilleures performances.
Les expériences ont comparé les performances de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA et de la recherche aléatoire (RS) au sein du benchmark MoRobtrol. Les résultats montrent que TensorRVEA a obtenu les meilleures performances globales, atteignant les valeurs HV les plus élevées et démontrant une bonne diversité de solutions dans plusieurs environnements. TensorMOEA/D a montré une forte adaptabilité dans les tâches à grande échelle, excellant particulièrement dans la cohérence des préférences des solutions. TensorNSGA-III et TensorHypE ont montré des performances similaires et étaient compétitifs sur plusieurs tâches. Dans l’ensemble, les algorithmes tensorisés basés sur la décomposition ont démontré des avantages supérieurs dans la résolution de problèmes à grande échelle et complexes.
Conclusion et travaux futurs Cette étude propose une méthodologie de représentation tensorisée pour remédier aux limitations des algorithmes EMO traditionnels basés sur CPU en termes d’efficacité computationnelle et d’évolutivité. L’approche a été appliquée à plusieurs algorithmes représentatifs, notamment NSGA-III, MOEA/D et HypE, atteignant des améliorations de performances significatives sur GPU tout en maintenant la qualité des solutions. Pour valider son applicabilité pratique, l’équipe a également développé MoRobtrol, une suite de benchmarks de contrôle robotique multi-objectif qui reformule les tâches de contrôle robotique dans des environnements de simulation physique en problèmes d’optimisation multi-objectif. Les résultats démontrent le potentiel des algorithmes tensorisés dans des scénarios à forte intensité computationnelle tels que l’intelligence incarnée. Bien que la méthode de tensorisation ait considérablement amélioré l’efficacité algorithmique, il reste des marges d’amélioration. Les directions futures incluent l’amélioration des opérateurs fondamentaux tels que le tri non dominé, la conception de nouvelles opérations tensorisées pour les systèmes multi-GPU, et l’intégration de données à grande échelle et de techniques d’apprentissage profond pour améliorer davantage les performances sur les problèmes d’optimisation à grande échelle.
Code open source / Ressources communautaires
Article :
https://arxiv.org/abs/2503.20286
GitHub :
https://github.com/EMI-Group/evomo
Projet amont (EvoX) :
https://github.com/EMI-Group/evox
Groupe QQ : 297969717

EvoMO est construit sur le framework EvoX. Si vous souhaitez en savoir plus sur EvoX, n’hésitez pas à consulter l’article officiel sur EvoX 1.0 publié sur notre compte public WeChat pour plus de détails.


