透過張量化橋接演化多目標最佳化
與GPU加速
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
隨著工程設計和能源管理等領域對複雜最佳化解決方案的需求持續增長,演化多目標最佳化(EMO)算法因其在解決多目標問題方面的強大能力而受到廣泛關注。然而,隨著最佳化任務規模和複雜度的增加,傳統基於 CPU 的 EMO 算法面臨顯著的效能瓶頸。
為了解決這一限制,EvoX 團隊提出透過張量化方法在 GPU 上平行化 EMO 算法。利用這一方法,他們成功設計並實現了多個 GPU 加速的 EMO 算法。此外,團隊還開發了 「MoRobtrol」,一個基於 Brax 物理引擎的多目標機器人控制基準測試套件,旨在系統性地評估 GPU 加速 EMO 算法的效能。
基於這些研究進展,EvoX 團隊發佈了 EvoMO,一個高效能的 GPU 加速 EMO 算法函式庫。相應的原始碼已在 GitHub 上公開:https://github.com/EMl-Group/evomo
張量化方法
在計算最佳化領域,張量是指一種能夠表示純量、向量、矩陣和更高階資料的多維陣列資料結構。張量化是將算法中的資料結構和操作轉換為張量形式的過程,使算法能夠充分利用 GPU 的平行運算能力。
在 EMO 算法中,所有關鍵資料結構都可以用張量化格式表示。種群中的個體可以用解張量 X 表示,其中每個行向量對應一個個體。目標函數值構成目標張量 F。此外,參考向量和權重向量等輔助資料結構可以分別表示為張量 R 和 W。這種統一的張量表示使得在表示層面實現種群級別的操作成為可能,為大規模平行運算奠定了堅實的基礎。
EMO 算法操作的張量化對於提升計算效率至關重要,可分為兩個層次:基本張量操作和控制流張量化。基本張量操作構成了 EMO 算法張量化實現的核心,詳見表 I。
表 I:基本張量操作

控制流張量化用可平行化的張量操作取代傳統的迴圈和條件邏輯。例如,for/while 迴圈可以透過廣播機制或高階函數(如 vmap)轉換為批次操作。同樣,if-else 條件判斷可以用遮罩技術取代,其中邏輯條件被編碼為布林張量,實現不同計算路徑之間的靈活切換。
與傳統 EMO 算法實現相比,張量化方法具有顯著優勢。首先,它提供了更大的靈活性,能夠自然地處理多維資料,而傳統方法通常僅限於二維矩陣操作。其次,張量化透過平行執行顯著提升了計算效率,避免了顯式迴圈和條件分支帶來的開銷。最後,它簡化了程式碼結構,使程式更加簡潔且易於維護。
如圖 1 所示,例如,Pareto 支配檢測的傳統實現依賴巢狀迴圈來進行逐元素比較。相比之下,張量化版本透過廣播和遮罩操作實現了相同的功能,實現了平行評估。這不僅降低了程式碼複雜度,還大幅提升了運行效能。

圖 1:傳統與基於張量的 Pareto 支配檢測實現的比較。
從更深層的角度來看,張量化非常適合 GPU 加速,因為 GPU 擁有大量平行核心,其單指令多執行緒(SIMT)架構與張量運算天然契合,尤其擅長矩陣操作。NVIDIA 的 Tensor Cores 等專用硬體進一步提升了張量操作的吞吐量。一般而言,具有高平行性、包含獨立計算任務且條件分支較少的算法更適合張量化。對於像 MOEA/D 這樣涉及順序依賴的算法,其固有結構對直接張量化構成挑戰。然而,透過結構重構和關鍵計算的解耦,仍然可以實現有效的平行加速。
算法張量化的應用範例
基於張量化表示方法,EvoX 團隊設計並實現了三種經典 EMO 算法的張量化版本:基於支配的 NSGA-III、基於分解的 MOEA/D 和基於指標的 HypE。以下部分以 MOEA/D 為例進行詳細說明。NSGA-III 和 HypE 的張量化實現可在參考論文中找到。
如圖 2 所示,傳統的 MOEA/D 將多目標問題分解為多個子問題,每個子問題獨立最佳化。算法包含四個核心步驟:交叉和變異、適應度評估、理想點更新和鄰域更新。這些步驟在單個迴圈中對每個個體依序執行。這種順序處理在處理大規模種群時會導致大量的計算開銷,因為每個個體必須按順序完成所有步驟,限制了 GPU 加速的潛在收益。特別是鄰域更新依賴於個體之間的交互,這進一步增加了平行化的難度。

圖 2:MOEA/D 的偽代碼
為了解決傳統 MOEA/D 中的順序依賴問題,團隊在環境選擇的內部迴圈中引入了張量化表示方法。透過將交叉和變異、適應度評估、理想點更新和鄰域更新解耦,這些元件被視為獨立操作。這使得所有個體的平行處理成為可能,從而構建了張量化的 MOEA/D 算法,稱為 TensorMOEA/D。在該算法中,環境選擇分為兩個主要階段:比較和種群更新,以及精英解選擇。這兩個階段主要透過兩次 vmap 操作進行張量化。詳細過程如圖 3 所示。
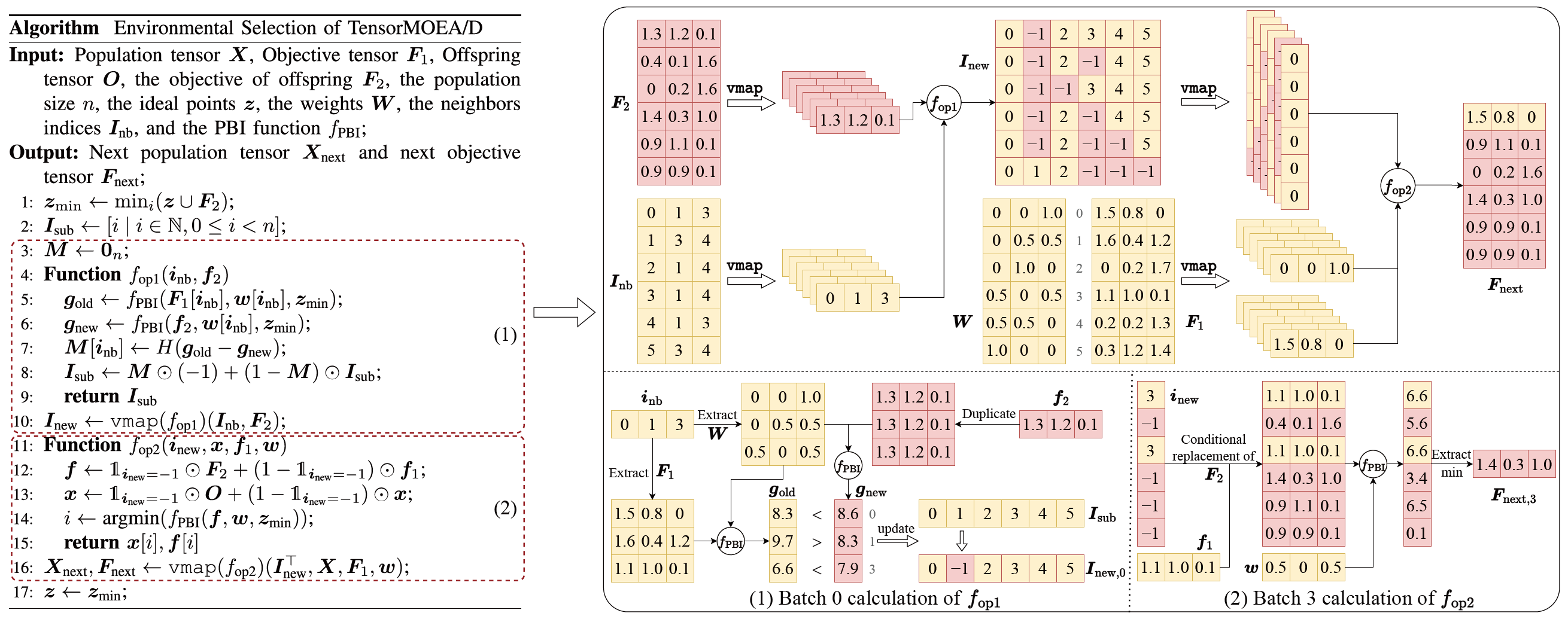
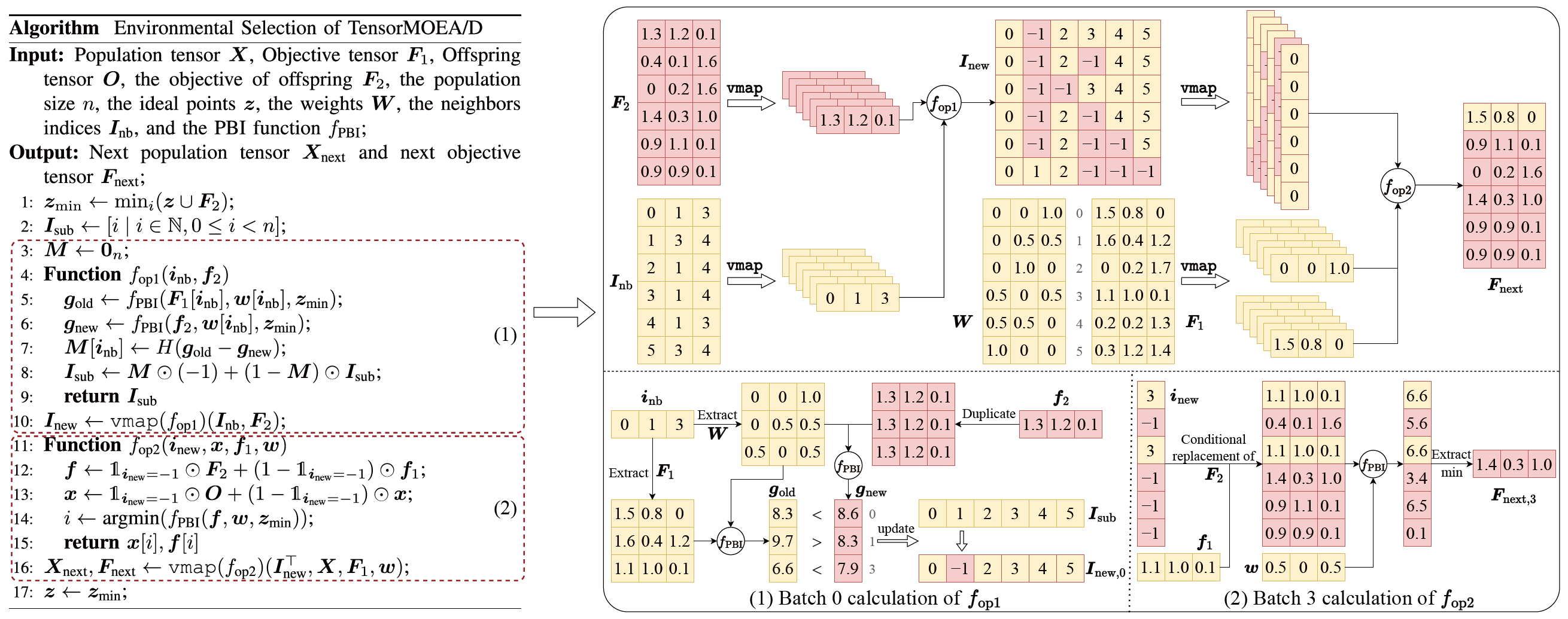
圖 3:TensorMOEA/D 算法中環境選擇的概覽。左:算法的偽代碼。右:模組 (1) 和模組 (2) 的張量資料流。右圖上部顯示了模組 (1) 和 (2) 的整體張量資料流,下部展示了批次計算的張量資料流,左側為模組 (1),右側為模組 (2)。
為了更全面地理解張量化在 EMO 算法中的價值,可以從三個角度進行總結。首先,張量化實現了從數學公式到高效程式碼的直接轉換,縮小了算法設計與實現之間的差距。例如,圖 4 展示了張量化的非支配排序程序如何從偽代碼直接轉譯為 Python 程式碼。其次,張量化透過將種群級別的操作統一為單一張量表示,顯著簡化了程式碼結構。這減少了對迴圈和條件語句的依賴,從而提升了程式碼的可讀性和可維護性。第三,張量化增強了算法的可重現性。其結構化的表示有助於比較測試和結果的一致重現。

圖 4:張量化非支配排序從偽代碼(左)到 Python 程式碼(右)的無縫轉換。
效能展示
為了評估 GPU 加速多目標最佳化算法的效能,EvoX 團隊系統性地進行了三類實驗,分別聚焦於計算加速、數值最佳化效能以及多目標機器人控制任務的有效性。
計算加速效能:
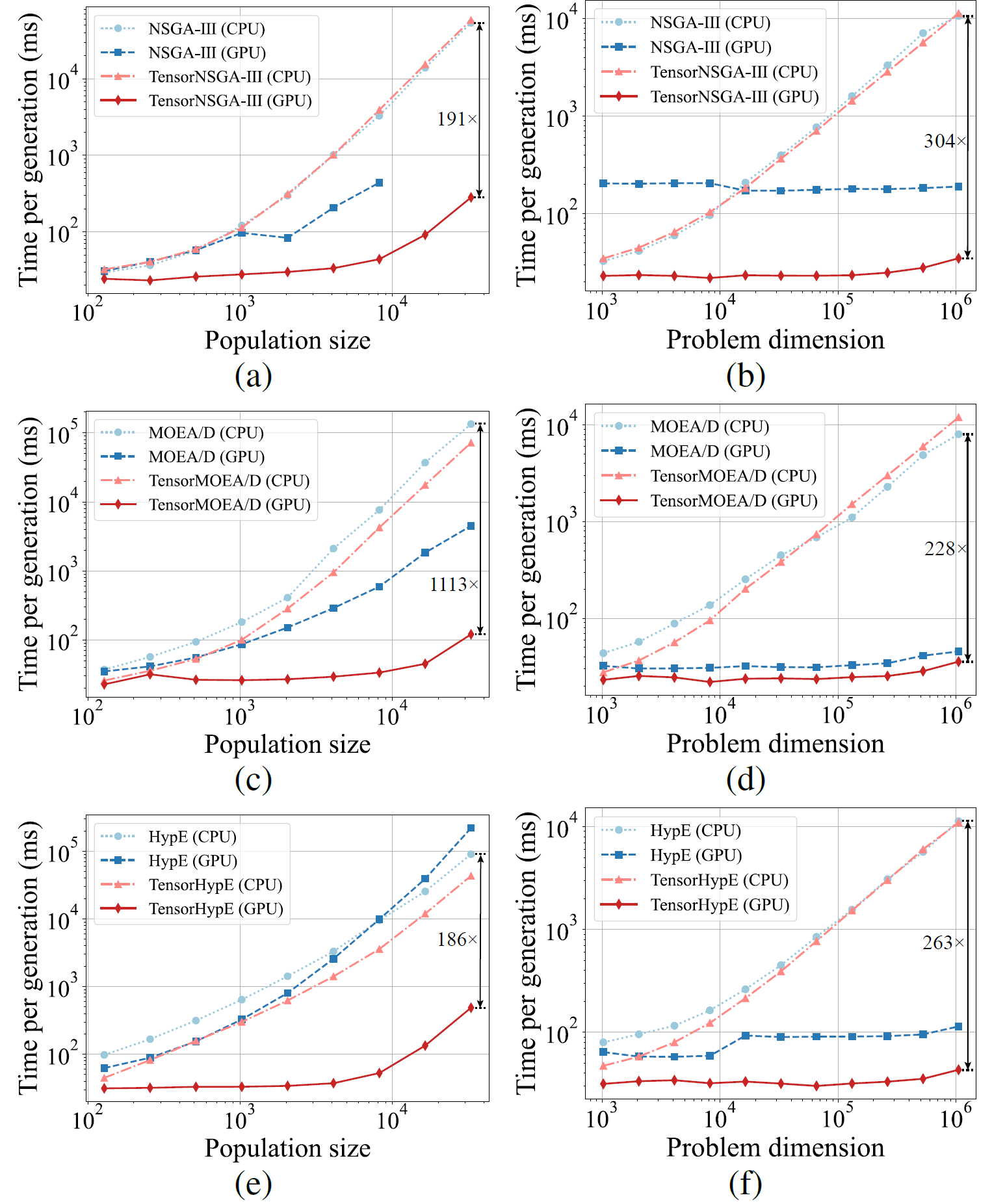
圖 5:NSGA-III、MOEA/D 和 HypE 與其張量化版本在 CPU 和 GPU 平台上,不同種群大小和問題維度下的加速效能比較。
實驗結果顯示,TensorNSGA-III、TensorMOEA/D 和 TensorHypE 在 GPU 上相比其非張量化的 CPU 版本實現了顯著更高的執行速度。隨著種群大小和問題維度的增加,觀察到的最大加速比高達 1113 倍。張量化算法在處理大規模計算任務時展現出優異的可擴展性和穩定性——其運行時間僅略有增加,同時保持一致的高效能。這些發現凸顯了張量化在多目標最佳化 GPU 加速方面的顯著優勢。
LSMOP 測試套件上的效能:
表 II:非張量化和張量化 EMO 算法在 LSMOP1—LSMOP9 上的 IGD 和運行時間(秒)統計結果(均值和標準差)。所有實驗均在 RTX 4090 GPU 上進行,最佳結果已標示。
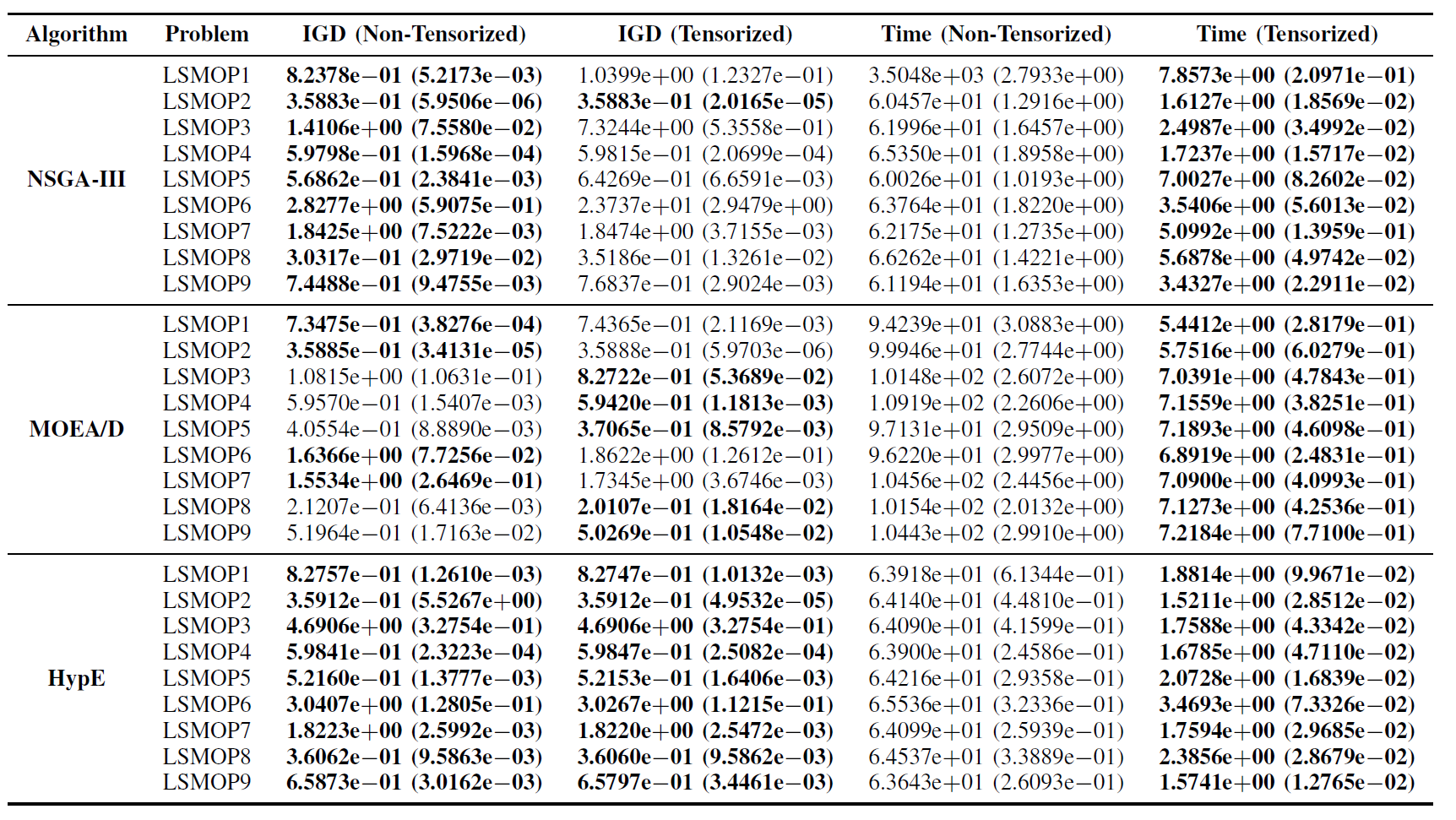
實驗結果表明,基於張量化表示的 GPU 加速 EMO 算法在顯著提升計算效率的同時,維持了甚至在某些情況下超越了其原始版本的最佳化精度。
多目標機器人控制任務:
為了全面評估 GPU 加速 EMO 算法的實際效能,團隊開發了一個名為 MoRobtrol 的多目標機器人控制基準測試套件。該套件包含的任務列於表 III。
表 III:所提出的 MoRobtrol 基準測試套件中多目標機器人控制問題概覽
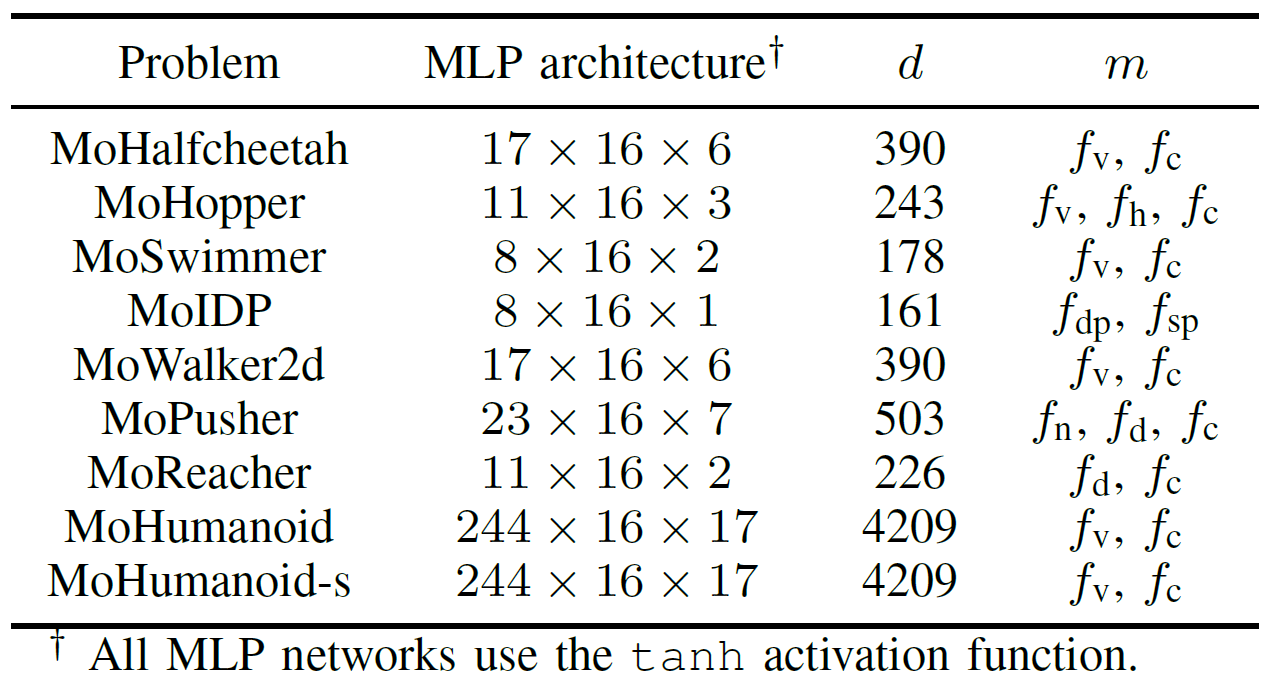
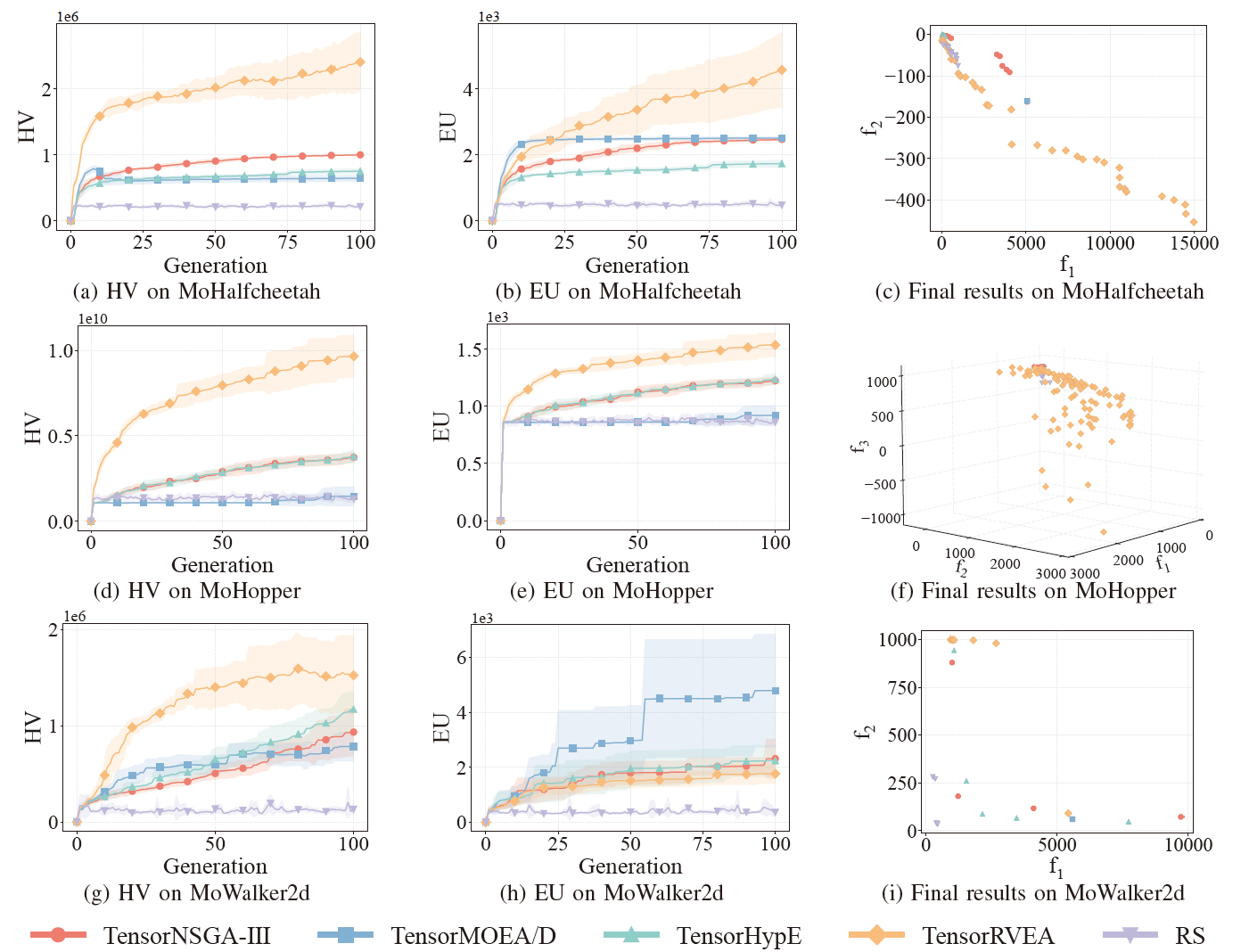
圖 6:TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和隨機搜索(RS)在不同問題上的比較效能(HV、EU 和最終結果視覺化):MoHalfcheetah(390D)、MoHopper(243D)和 MoWalker2d(390D)。注:所有指標值越高表示效能越好。
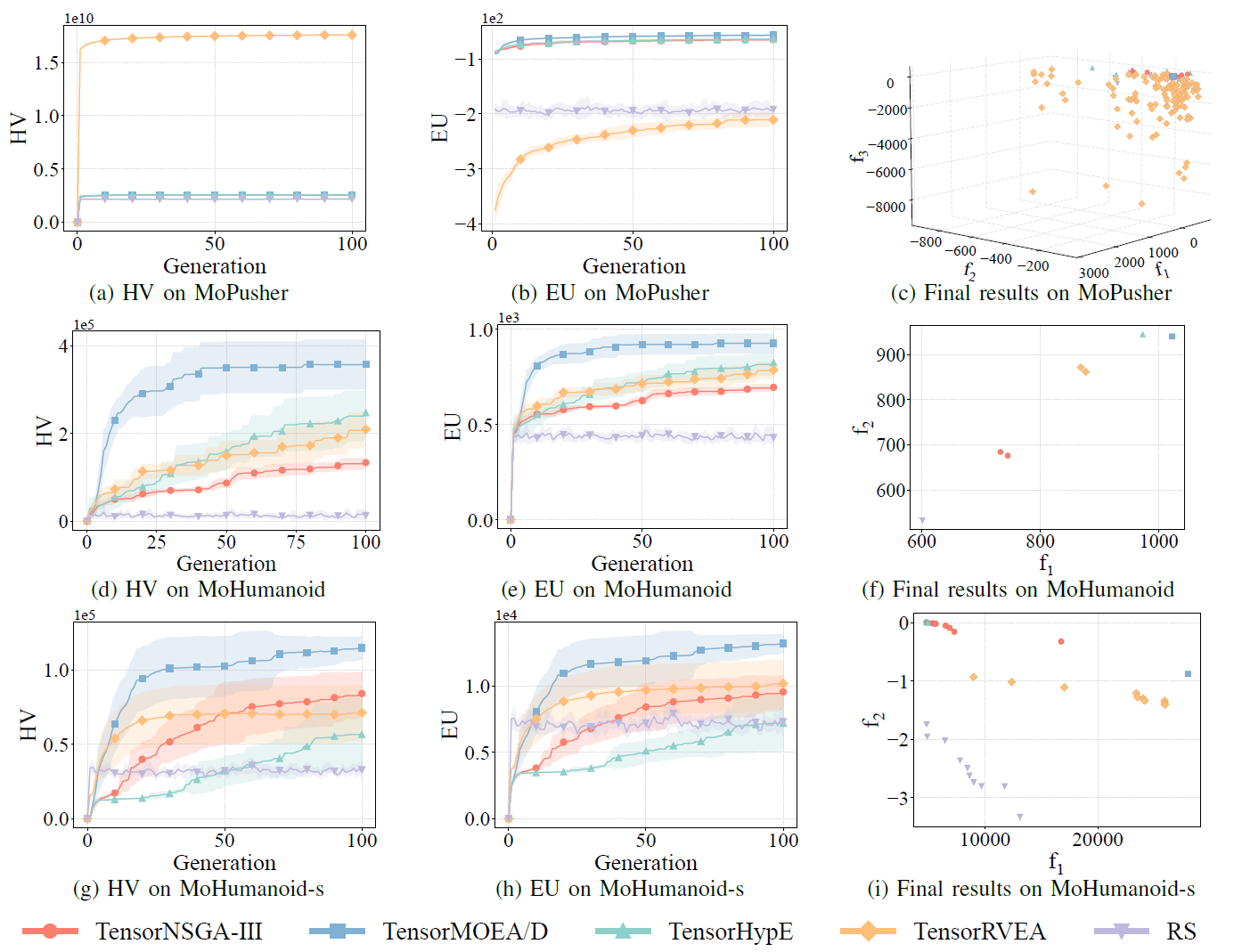
圖 7:TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和隨機搜索(RS)在不同問題上的比較效能(HV、EU 和最終結果視覺化):MoPusher(503D)、MoHumanoid(4209D)和 MoHumanoid-s(4209D)。注:所有指標值越高表示效能越好。
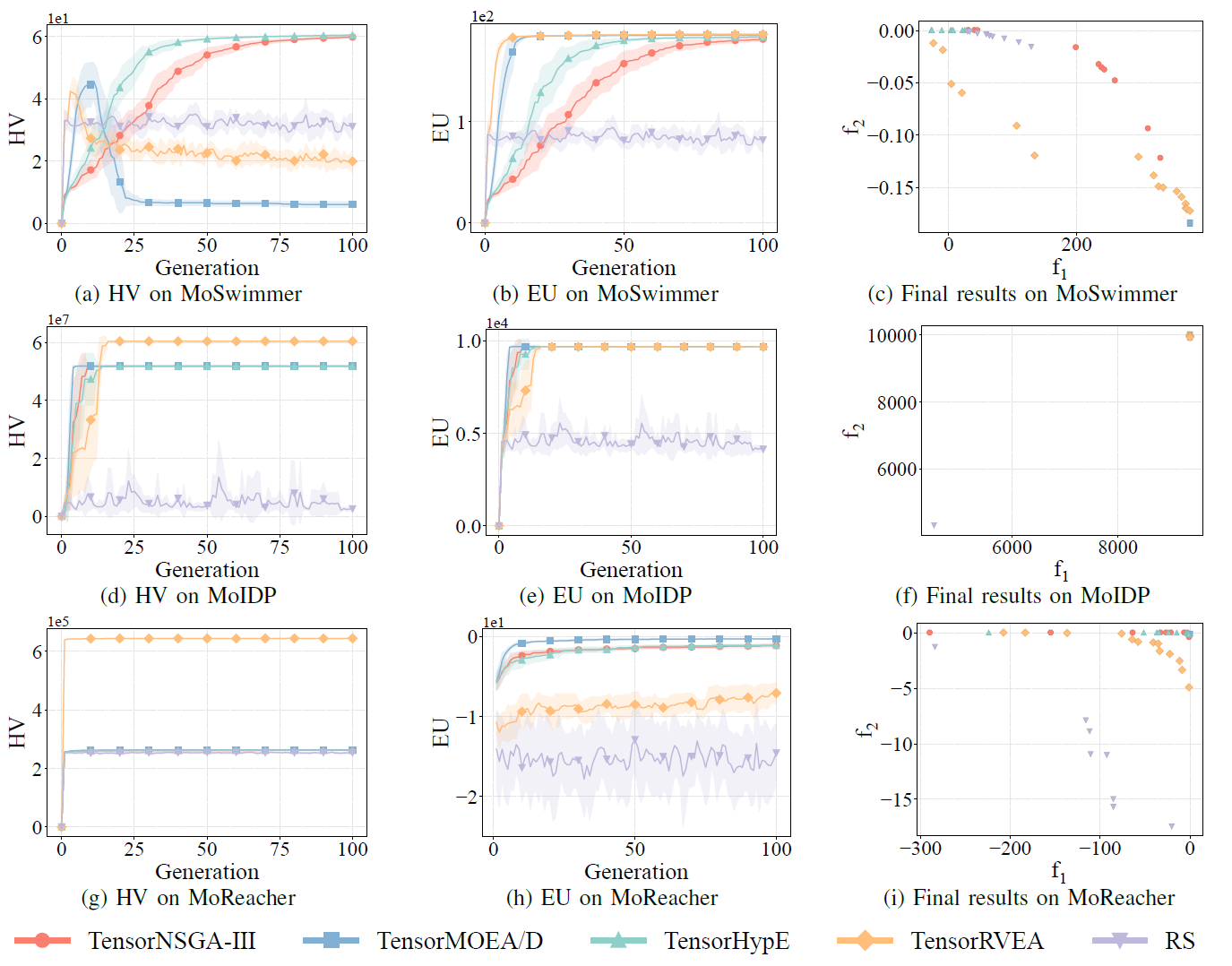
圖 8:TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和隨機搜索(RS)在不同問題上的比較效能(HV、EU 和最終結果視覺化):MoSwimmer(178D)、MoIDP(161D)和 MoReacher(226D)。注:所有指標值越高表示效能越好。
實驗比較了 TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和隨機搜索(RS)在 MoRobtrol 基準測試中的效能。結果顯示,TensorRVEA 取得了最佳的整體效能,在多個環境中獲得了最高的 HV 值並展現出良好的解多樣性。TensorMOEA/D 在大規模任務中表現出強大的適應性,尤其在解的偏好一致性方面表現突出。TensorNSGA-III 和 TensorHypE 表現相近,在多個任務上具有競爭力。總體而言,張量化的基於分解的算法在解決大規模和複雜問題方面展現出更優越的優勢。
結論與未來工作 本研究提出了一種張量化表示方法,以解決傳統基於 CPU 的 EMO 算法在計算效率和可擴展性方面的限制。該方法已應用於多個代表性算法,包括 NSGA-III、MOEA/D 和 HypE,在 GPU 上實現了顯著的效能提升,同時保持了解的品質。為了驗證其實際適用性,團隊還開發了 MoRobtrol,一個多目標機器人控制基準測試套件,將物理模擬環境中的機器人控制任務重新表述為多目標最佳化問題。結果展示了張量化算法在具身智慧等計算密集型場景中的潛力。儘管張量化方法已大幅提升了算法效率,但仍有進一步增強的空間。未來方向包括改進非支配排序等核心運算子、為多 GPU 系統設計新的張量化操作,以及整合大規模資料和深度學習技術以進一步提升大規模最佳化問題的效能。
開源程式碼 / 社群資源
論文:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
上游專案(EvoX):
https://github.com/EMI-Group/evox
QQ群:297969717

EvoMO 建立在 EvoX 框架之上。如果您有興趣了解更多關於 EvoX 的資訊,歡迎查閱我們微信公眾號上發佈的 EvoX 1.0 官方文章以獲取更多詳情。


