桥接进化多目标优化
与基于张量化的GPU加速
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
随着工程设计和能源管理等领域对复杂优化解决方案的需求持续增长,进化多目标优化(EMO)算法因其在求解多目标问题方面的强大能力而受到广泛关注。然而,随着优化任务规模和复杂度的增加,传统基于 CPU 的 EMO 算法面临着显著的性能瓶颈。
为解决这一局限性,EvoX 团队提出通过张量化方法在 GPU 上并行化 EMO 算法。利用该方法,他们成功设计并实现了多个 GPU 加速的 EMO 算法。此外,团队还开发了 “MoRobtrol”,一个基于 Brax 物理引擎的多目标机器人控制基准测试套件,旨在系统评估 GPU 加速 EMO 算法的性能。
基于这些研究进展,EvoX 团队发布了 EvoMO,一个高性能的 GPU 加速 EMO 算法库。相应的源代码已在 GitHub 上公开:https://github.com/EMl-Group/evomo
张量化方法
在计算优化领域,张量是指一种能够表示标量、向量、矩阵和更高阶数据的多维数组数据结构。张量化是将算法中的数据结构和操作转换为张量形式的过程,使算法能够充分利用 GPU 的并行计算能力。
在 EMO 算法中,所有关键数据结构都可以用张量化格式表示。种群中的个体可以用解张量 X 表示,其中每个行向量对应一个个体。目标函数值构成目标张量 F。此外,参考向量和权重向量等辅助数据结构可以分别表示为张量 R 和 W。这种统一的张量表示在表示层面实现了种群级别的操作,为大规模并行计算奠定了坚实基础。
EMO 算法操作的张量化对于提升计算效率至关重要,可分为两个层次:基本张量操作和控制流张量化。基本张量操作构成了 EMO 算法张量化实现的核心,详见表 I。
表 I:基本张量操作

控制流张量化用可并行化的张量操作替代传统的循环和条件逻辑。例如,for/while 循环可以通过广播机制或高阶函数(如 vmap)转换为批量操作。类似地,if-else 条件语句可以用掩码技术替代,其中逻辑条件被编码为布尔张量,实现不同计算路径之间的灵活切换。
与传统 EMO 算法实现相比,张量化方法具有显著优势。首先,它提供了更大的灵活性,能够自然地处理多维数据,而传统方法通常局限于二维矩阵操作。其次,张量化通过并行执行显著提升了计算效率,避免了显式循环和条件分支带来的开销。最后,它简化了代码结构,使程序更加简洁和易于维护。
如图 1 所示,传统的 Pareto 支配检测实现依赖嵌套循环进行逐元素比较。相比之下,张量化版本通过广播和掩码操作实现了相同的功能,支持并行评估。这不仅降低了代码复杂度,还大幅提升了运行时性能。

图1:传统实现与基于张量的 Pareto 支配检测实现的比较。
从更深层次来看,张量化非常适合 GPU 加速,因为 GPU 拥有大量并行核心,其单指令多线程(SIMT)架构与张量计算天然契合,尤其擅长矩阵运算。NVIDIA 的 Tensor Cores 等专用硬件进一步提升了张量操作的吞吐量。一般而言,具有高并行性、包含独立计算任务且条件分支较少的算法更适合张量化。对于像 MOEA/D 这样涉及顺序依赖的算法,其固有结构对直接张量化构成挑战。然而,通过结构重构和关键计算的解耦,仍然可以实现有效的并行加速。
算法张量化应用示例
基于张量化表示方法,EvoX 团队设计并实现了三种经典 EMO 算法的张量化版本:基于支配的 NSGA-III、基于分解的 MOEA/D 和基于指标的 HypE。以下以 MOEA/D 为例进行详细说明。NSGA-III 和 HypE 的张量化实现可参见相关论文。
如图 2 所示,传统 MOEA/D 将多目标问题分解为多个子问题,每个子问题独立优化。算法包含四个核心步骤:交叉变异、适应度评估、理想点更新和邻域更新。这些步骤在单个循环中对每个个体顺序执行。这种顺序处理方式在处理大规模种群时会导致大量计算开销,因为每个个体必须按顺序完成所有步骤,限制了 GPU 加速的潜在收益。特别是邻域更新依赖于个体之间的交互,这进一步增加了并行化的难度。

图2:MOEA/D 的伪代码
为解决传统 MOEA/D 中的顺序依赖问题,团队在环境选择的内部循环中引入了张量化表示方法。通过将交叉变异、适应度评估、理想点更新和邻域更新解耦为独立操作,实现了所有个体的并行处理,从而构建了张量化的 MOEA/D 算法,称为 TensorMOEA/D。在该算法中,环境选择分为两个主要阶段:比较与种群更新,以及精英解选择。这两个阶段主要通过两次 vmap 操作实现张量化。详细过程如图 3 所示。
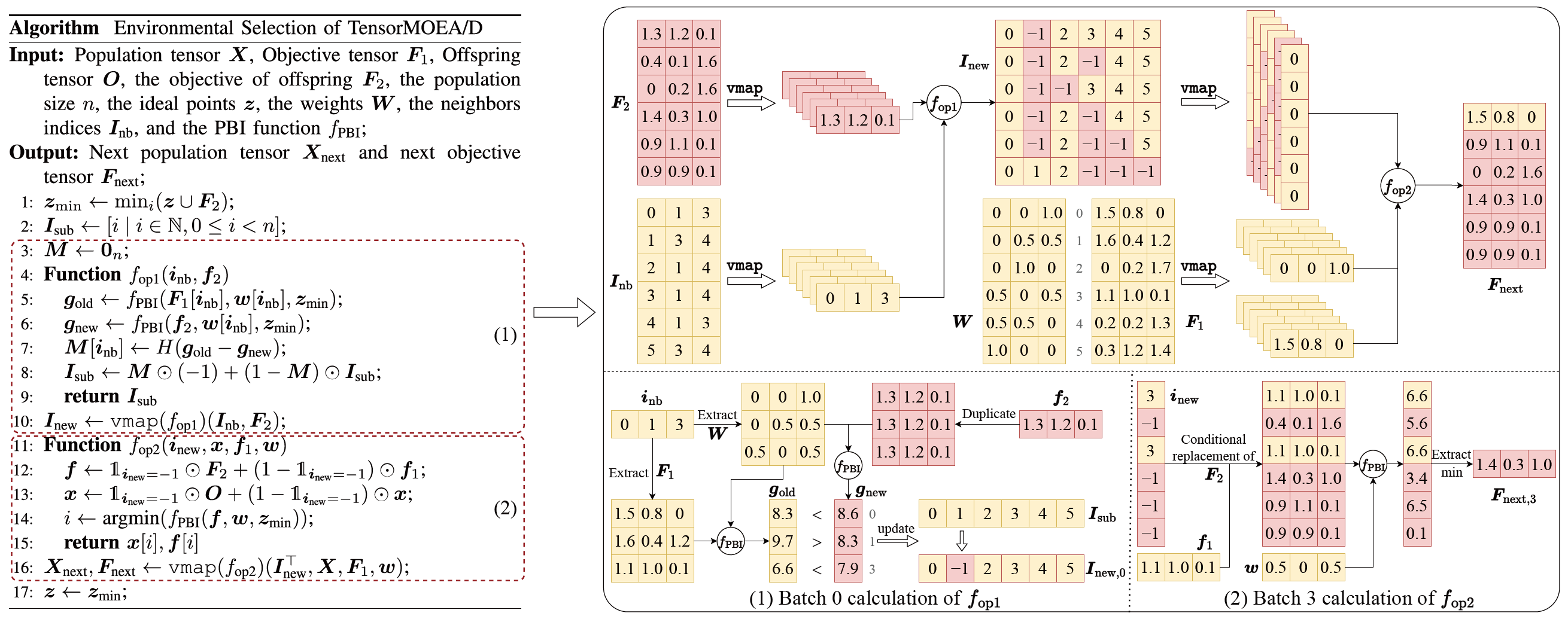
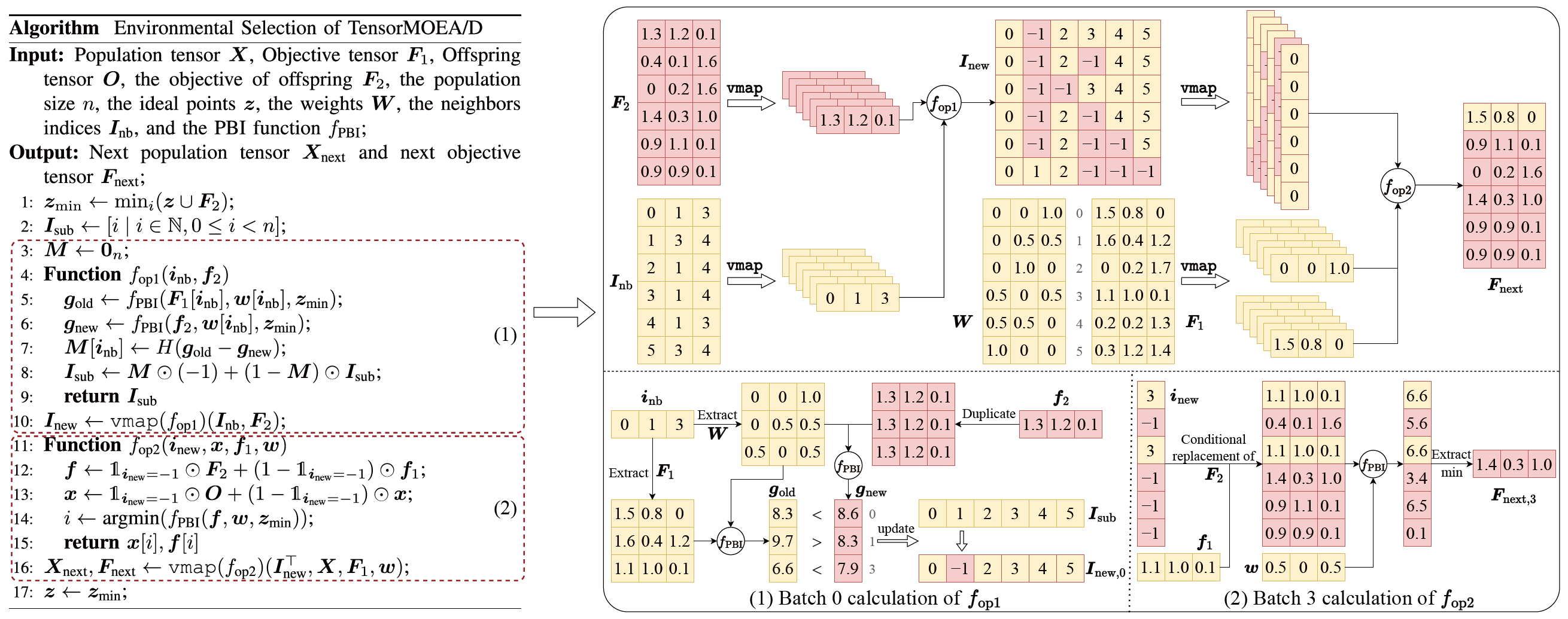
图3:TensorMOEA/D 算法中环境选择的概览。左:算法伪代码。右:模块 (1) 和模块 (2) 的张量数据流。右图上部展示了模块 (1) 和 (2) 的整体张量数据流,下部展示了批量计算的张量数据流,左侧为模块 (1),右侧为模块 (2)。
为更全面地理解张量化在 EMO 算法中的价值,可以从三个角度进行总结。首先,张量化实现了从数学公式到高效代码的直接转换,缩小了算法设计与实现之间的差距。例如,图 4 展示了张量化的非支配排序过程如何从伪代码直接转换为 Python 代码。其次,张量化通过将种群级别的操作统一为单一的张量表示,显著简化了代码结构。这减少了对循环和条件语句的依赖,从而提高了代码的可读性和可维护性。第三,张量化增强了算法的可复现性。其结构化表示有助于对比测试和结果的一致复现。

图4:张量化非支配排序从伪代码(左)到 Python 代码(右)的无缝转换。
性能展示
为评估 GPU 加速多目标优化算法的性能,EvoX 团队系统地进行了三类实验,分别关注计算加速、数值优化性能和多目标机器人控制任务的有效性。
计算加速性能:
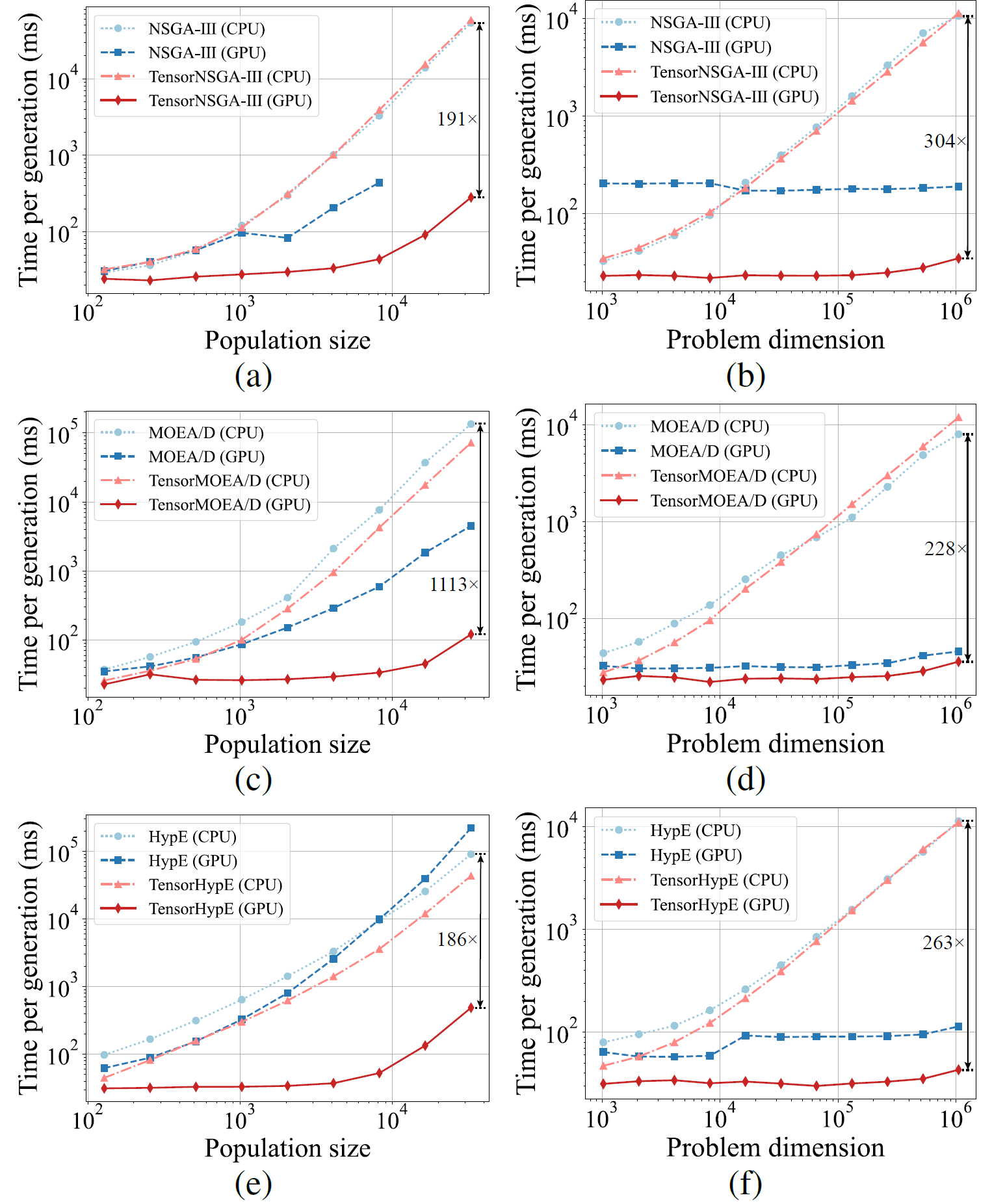
图5:NSGA-III、MOEA/D 和 HypE 与其张量化版本在 CPU 和 GPU 平台上不同种群大小和问题维度下的加速性能比较。
实验结果表明,TensorNSGA-III、TensorMOEA/D 和 TensorHypE 在 GPU 上相比其非张量化的 CPU 版本实现了显著更高的执行速度。随着种群大小和问题维度的增加,观察到的最大加速比高达 1113倍。张量化算法在处理大规模计算任务时展现出优异的可扩展性和稳定性——其运行时间仅略有增加,同时保持了一贯的高性能。这些发现凸显了张量化在多目标优化 GPU 加速方面的巨大优势。
LSMOP 测试套件上的性能:
表 II:非张量化和张量化 EMO 算法在 LSMOP1—LSMOP9 上的 IGD 和运行时间(秒)统计结果(均值和标准差)。所有实验均在 RTX 4090 GPU 上进行,最佳结果已标注。
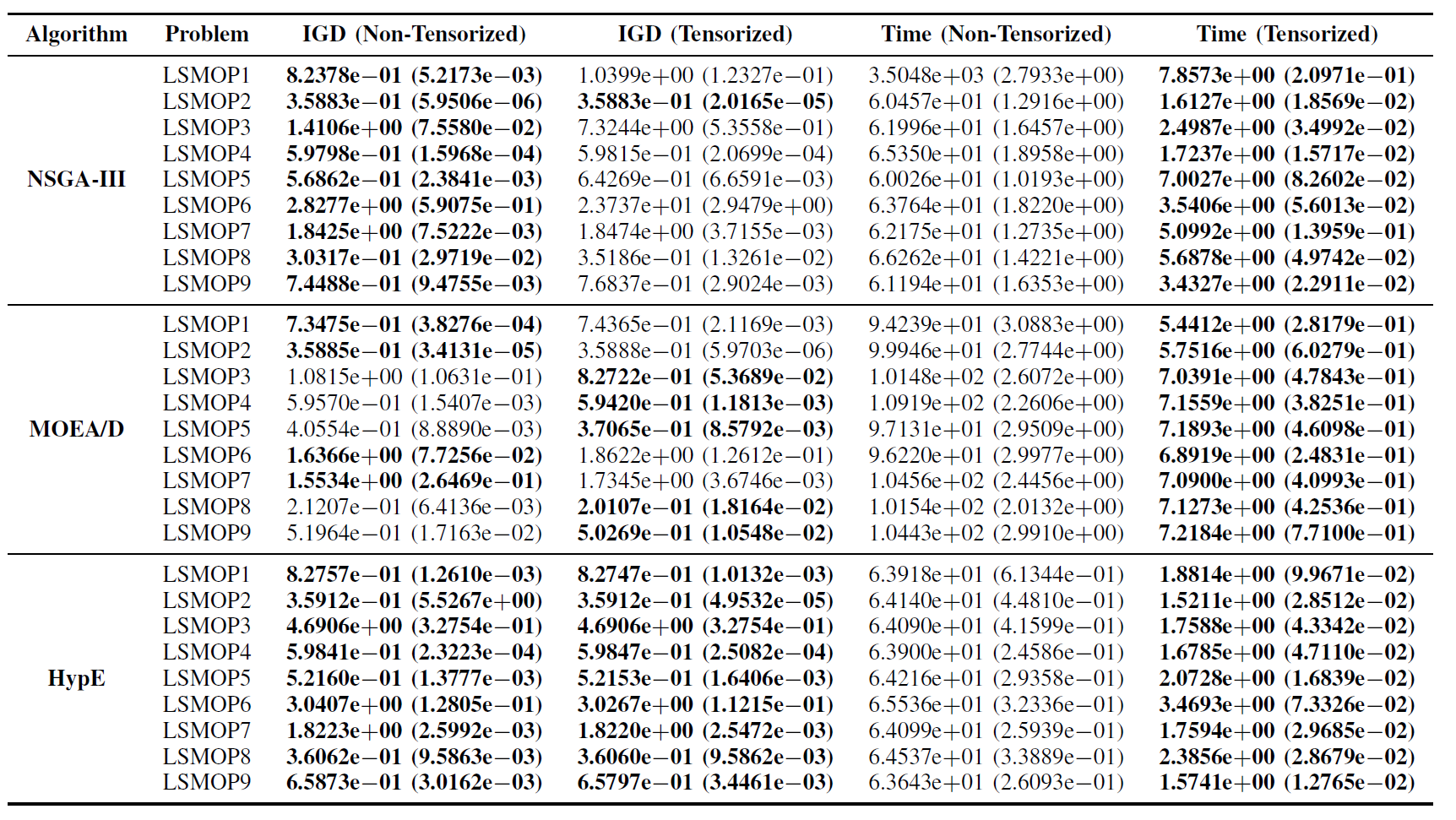
实验结果表明,基于张量化表示的 GPU 加速 EMO 算法在显著提升计算效率的同时,保持了甚至在某些情况下超越了原始算法的优化精度。
多目标机器人控制任务:
为全面评估 GPU 加速 EMO 算法的实际性能,团队开发了名为 MoRobtrol 的多目标机器人控制基准测试套件。该套件包含的任务列于表 III。
表 III:所提出的 MoRobtrol 基准测试套件中多目标机器人控制问题概览
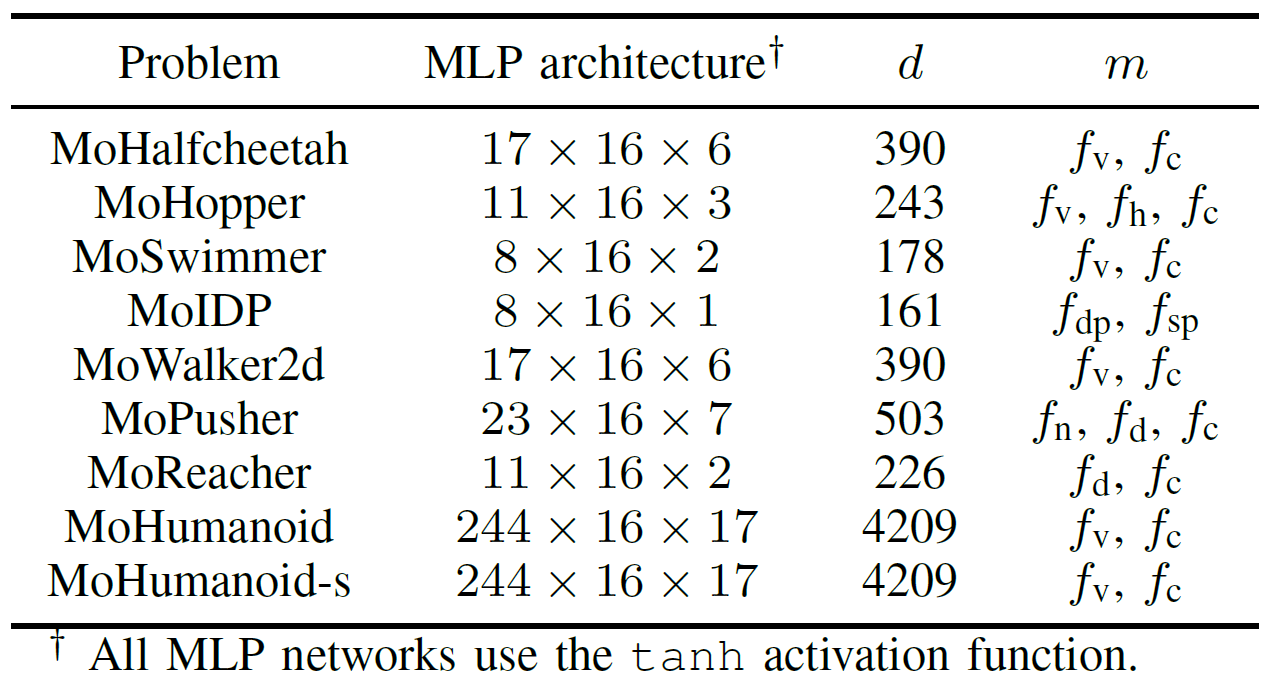
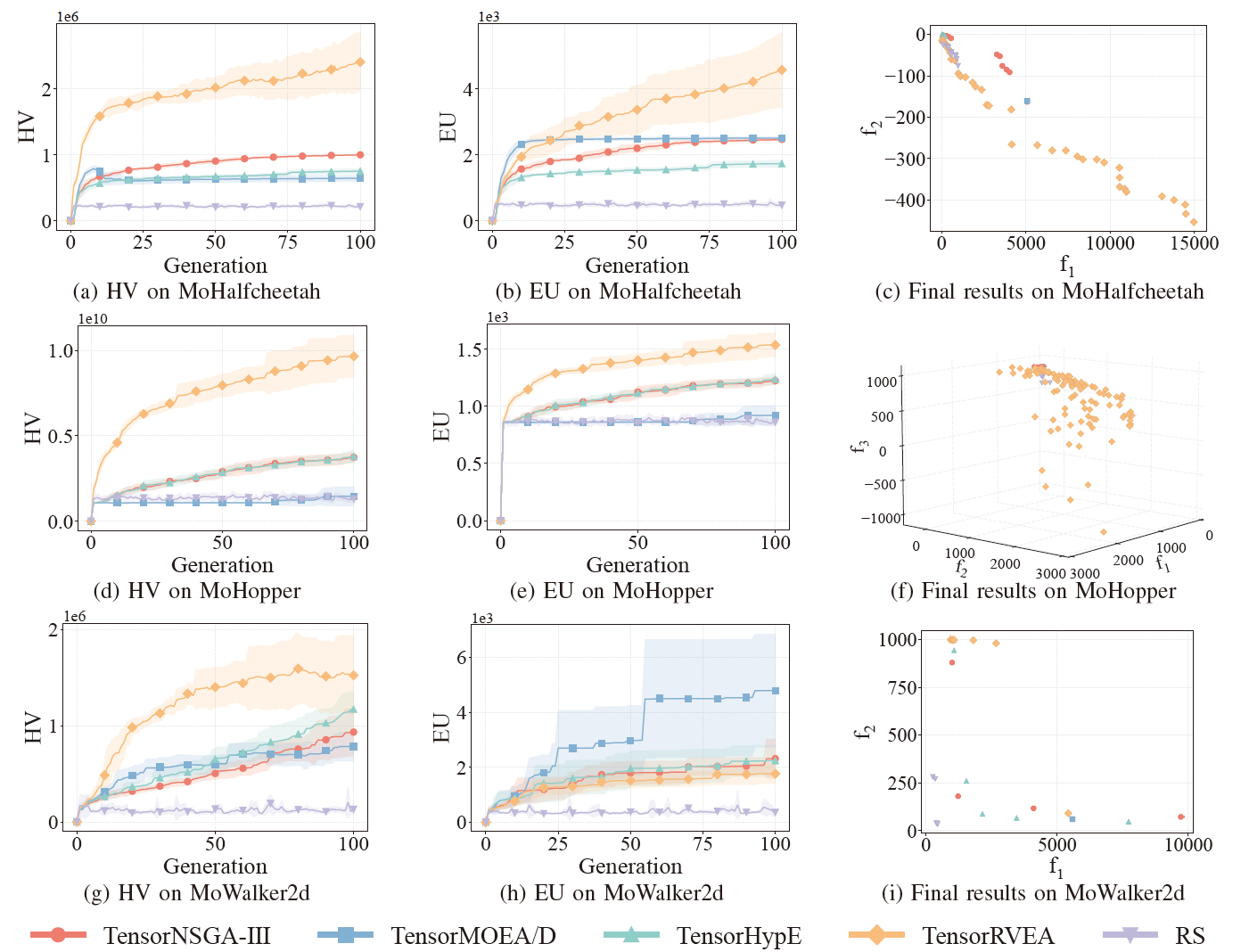
图6:TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和随机搜索(RS)在不同问题上的性能比较(HV、EU 和最终结果可视化):MoHalfcheetah (390D)、MoHopper (243D) 和 MoWalker2d (390D)。注:所有指标值越高表示性能越好。
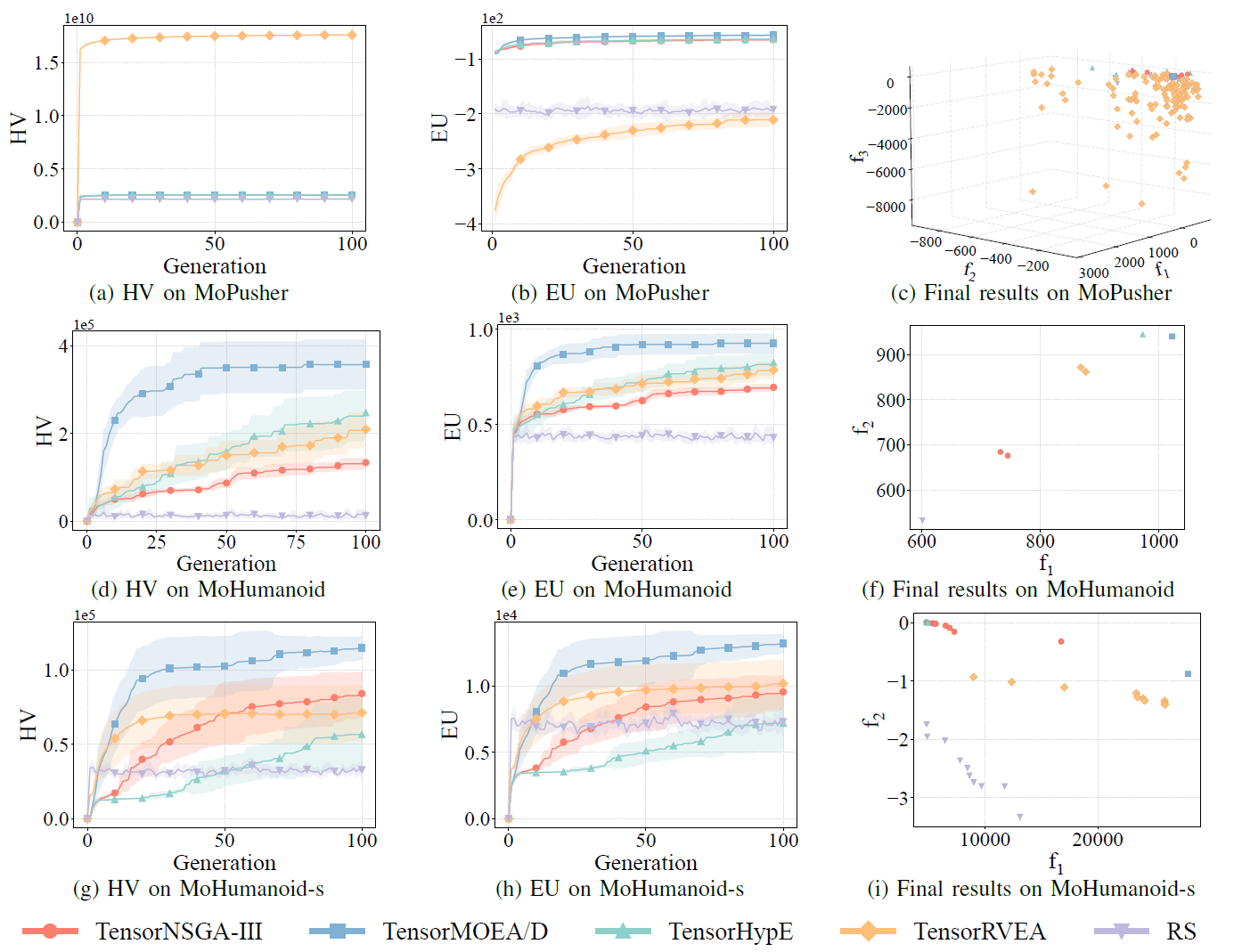
图7:TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和随机搜索(RS)在不同问题上的性能比较(HV、EU 和最终结果可视化):MoPusher (503D)、MoHumanoid (4209D) 和 MoHumanoid-s (4209D)。注:所有指标值越高表示性能越好。
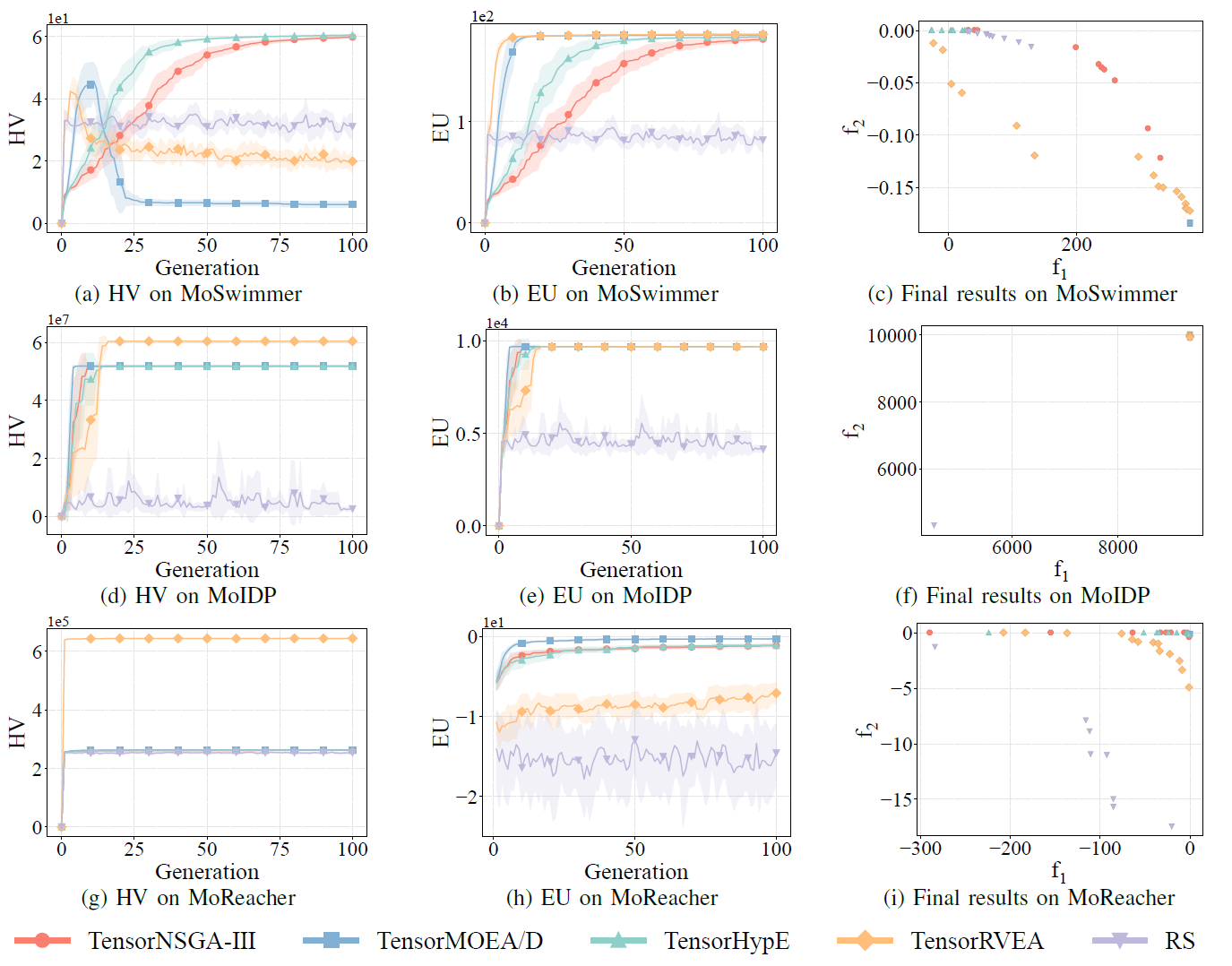
图8:TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和随机搜索(RS)在不同问题上的性能比较(HV、EU 和最终结果可视化):MoSwimmer (178D)、MoIDP (161D) 和 MoReacher (226D)。注:所有指标值越高表示性能越好。
实验比较了 TensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA 和随机搜索(RS)在 MoRobtrol 基准测试中的性能。结果表明,TensorRVEA 取得了最佳的整体性能,在多个环境中获得了最高的 HV 值并展现出良好的解多样性。TensorMOEA/D 在大规模任务中表现出强大的适应性,尤其在解的偏好一致性方面表现突出。TensorNSGA-III 和 TensorHypE 表现相近,在多个任务上具有竞争力。总体而言,张量化的基于分解的算法在求解大规模和复杂问题方面展现出更优越的优势。
结论与未来工作 本研究提出了一种张量化表示方法,以解决传统基于 CPU 的 EMO 算法在计算效率和可扩展性方面的局限性。该方法已应用于多个代表性算法,包括 NSGA-III、MOEA/D 和 HypE,在 GPU 上实现了显著的性能提升,同时保持了解的质量。为验证其实际适用性,团队还开发了 MoRobtrol,一个多目标机器人控制基准测试套件,将物理仿真环境中的机器人控制任务重新表述为多目标优化问题。结果展示了张量化算法在具身智能等计算密集型场景中的潜力。尽管张量化方法已大幅提升了算法效率,但仍有进一步提升的空间。未来方向包括改进非支配排序等核心算子、为多 GPU 系统设计新的张量化操作,以及整合大规模数据和深度学习技术以进一步提升大规模优化问题的性能。
开源代码 / 社区资源
论文:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
上游项目(EvoX):
https://github.com/EMI-Group/evox
QQ群:297969717

EvoMO 基于 EvoX 框架构建。如果您有兴趣了解更多关于 EvoX 的信息,欢迎查阅我们微信公众号上发布的 EvoX 1.0 官方文章了解更多详情。


