Связь эволюционной многокритериальной оптимизации
и GPU-ускорения через тензоризацию
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
С непрерывным ростом потребности в решении сложных задач оптимизации в таких областях, как инженерное проектирование и управление энергетикой, алгоритмы эволюционной многокритериальной оптимизации (EMO) привлекают широкое внимание благодаря своим надёжным возможностям решения многокритериальных задач. Однако по мере роста масштаба и сложности задач оптимизации традиционные EMO-алгоритмы на базе CPU сталкиваются со значительными узкими местами в производительности.
Для преодоления этого ограничения команда EvoX предложила распараллелить EMO-алгоритмы на GPU с помощью методологии тензоризации. Используя этот метод, они успешно разработали и реализовали несколько GPU-ускоренных EMO-алгоритмов. Кроме того, команда разработала «MoRobtrol» — набор бенчмарков для многокритериального управления роботами, построенный на физическом движке Brax, предназначенный для систематической оценки производительности GPU-ускоренных EMO-алгоритмов.
На основе этих исследовательских достижений команда EvoX выпустила EvoMO — высокопроизводительную GPU-ускоренную библиотеку EMO-алгоритмов. Соответствующий исходный код доступен на GitHub: https://github.com/EMl-Group/evomo
Методология тензоризации
В области вычислительной оптимизации тензор — это многомерная структура данных в виде массива, способная представлять скаляры, векторы, матрицы и данные более высокого порядка. Тензоризация — это процесс преобразования структур данных и операций алгоритма в тензорную форму, позволяющий алгоритму в полной мере использовать возможности параллельных вычислений GPU.
В EMO-алгоритмах все ключевые структуры данных могут быть выражены в тензоризованном формате. Особи популяции могут быть представлены тензором решений X, где каждый вектор-строка соответствует одной особи. Значения целевых функций образуют тензор целей F. Кроме того, вспомогательные структуры данных, такие как референсные векторы и весовые векторы, могут быть выражены как тензоры R и W соответственно. Это единое тензорное представление обеспечивает операции на уровне популяции на уровне представления, закладывая прочную основу для крупномасштабных параллельных вычислений.
Тензоризация операций EMO-алгоритмов имеет решающее значение для повышения вычислительной эффективности и может быть разделена на два уровня: базовые тензорные операции и тензоризация потока управления. Базовые тензорные операции составляют ядро тензоризованной реализации EMO-алгоритмов, как подробно описано в Таблице I.
Таблица I: Базовые тензорные операции

Тензоризация потока управления заменяет традиционную логику циклов и условий параллелизуемыми тензорными операциями. Например, циклы for/while могут быть преобразованы в пакетные операции с использованием механизмов трансляции (broadcasting) или функций высшего порядка, таких как vmap. Аналогично, условные конструкции if-else могут быть заменены техниками маскирования, где логические условия кодируются как булевы тензоры, обеспечивая гибкое переключение между различными путями вычислений.
По сравнению с традиционными реализациями EMO-алгоритмов подход тензоризации предлагает значительные преимущества. Во-первых, он обеспечивает большую гибкость, естественно обрабатывая многомерные данные, тогда как традиционные методы часто ограничены двумерными матричными операциями. Во-вторых, тензоризация значительно повышает вычислительную эффективность за счёт параллельного выполнения, избегая накладных расходов, связанных с явными циклами и условными переходами. Наконец, она упрощает структуру кода, делая программы более лаконичными и удобными для сопровождения.
Как показано на Рис. 1, например, традиционная реализация проверки доминирования по Парето опирается на вложенные циклы для поэлементного сравнения. Напротив, тензоризованная версия достигает той же функциональности через операции трансляции и маскирования, обеспечивая параллельную оценку. Это не только снижает сложность кода, но и значительно улучшает производительность во время выполнения.

Рис. 1: Сравнение традиционной и тензорной реализаций обнаружения доминирования по Парето.
С более глубокой точки зрения тензоризация хорошо подходит для GPU-ускорения, поскольку GPU обладают большим количеством параллельных ядер, а их архитектура «одна инструкция — множество потоков» (SIMT) естественно согласуется с тензорными вычислениями, особенно превосходя в матричных операциях. Специализированное оборудование, такое как Tensor Cores от NVIDIA, дополнительно повышает пропускную способность тензорных операций. В целом алгоритмы с высоким параллелизмом, содержащие независимые вычислительные задачи и минимальное условное ветвление, более пригодны для тензоризации. Для алгоритмов типа MOEA/D, которые включают последовательные зависимости, внутренняя структура создаёт трудности для прямой тензоризации. Однако через структурную рефакторизацию и разделение критических вычислений всё же возможно достичь эффективного параллельного ускорения.
Пример применения тензоризации алгоритмов
На основе методологии тензоризованного представления команда EvoX разработала и реализовала тензоризованные версии трёх классических EMO-алгоритмов: основанного на доминировании NSGA-III, основанного на декомпозиции MOEA/D и основанного на индикаторах HypE. В следующем разделе приводится подробное объяснение на примере MOEA/D. Тензоризованные реализации NSGA-III и HypE можно найти в упомянутой статье.
Как показано на Рис. 2, традиционный MOEA/D декомпозирует многокритериальную задачу на множество подзадач, каждая из которых оптимизируется независимо. Алгоритм включает четыре основных шага: кроссовер и мутация, оценка приспособленности, обновление идеальной точки и обновление окрестности. Эти шаги выполняются последовательно для каждой особи в рамках одного цикла. Такая последовательная обработка приводит к значительным вычислительным затратам при работе с большими популяциями, поскольку каждая особь должна завершить все шаги по порядку, ограничивая потенциальные преимущества GPU-ускорения. В частности, обновление окрестности зависит от взаимодействий между особями, что дополнительно усложняет параллелизацию.

Рис. 2: Псевдокод MOEA/D
Для решения проблемы последовательных зависимостей в традиционном MOEA/D команда ввела метод тензоризованного представления во внутренний цикл отбора среды. Разделив кроссовер и мутацию, оценку приспособленности, обновление идеальной точки и обновление окрестности, эти компоненты рассматриваются как независимые операции. Это позволяет параллельно обрабатывать все особи, что приводит к построению тензоризованного алгоритма MOEA/D, называемого TensorMOEA/D. В этом алгоритме отбор среды разделён на два основных этапа: сравнение и обновление популяции, а также отбор элитных решений. Эти два этапа тензоризуются главным образом через два применения операции vmap. Подробный процесс показан на Рис. 3.
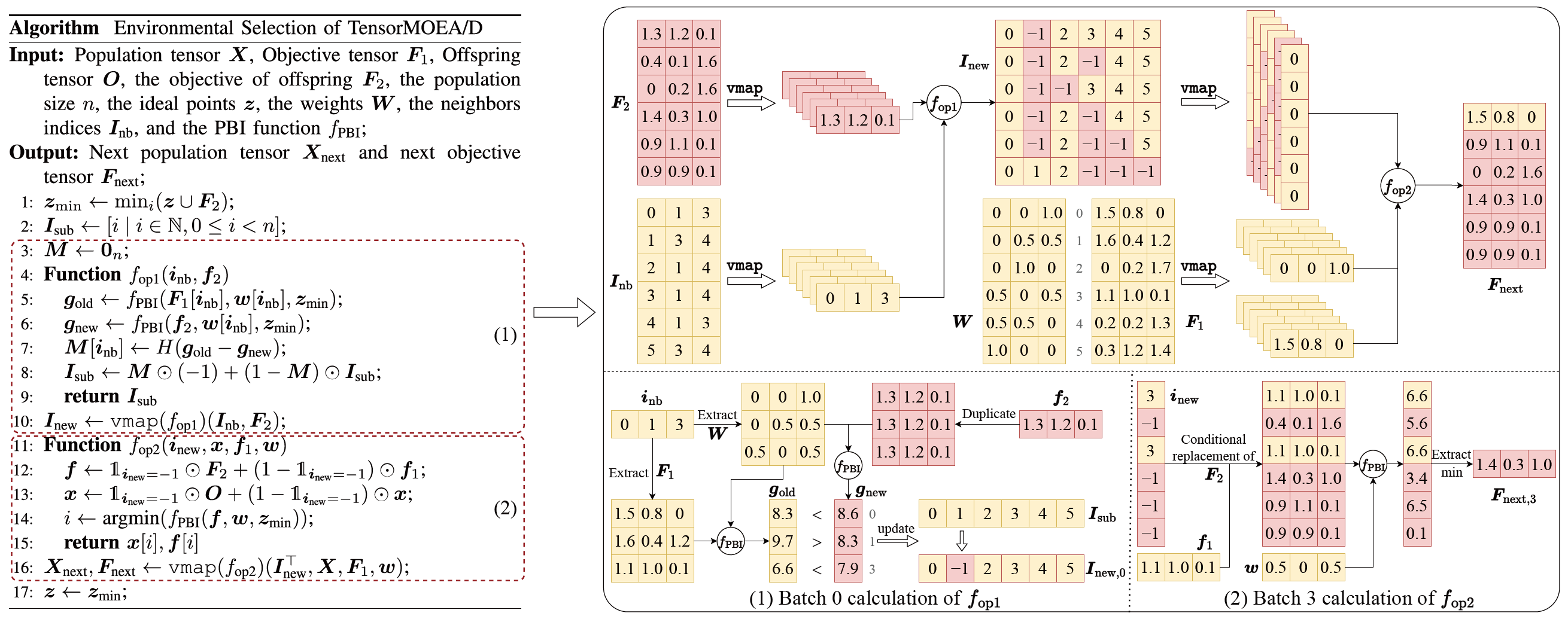
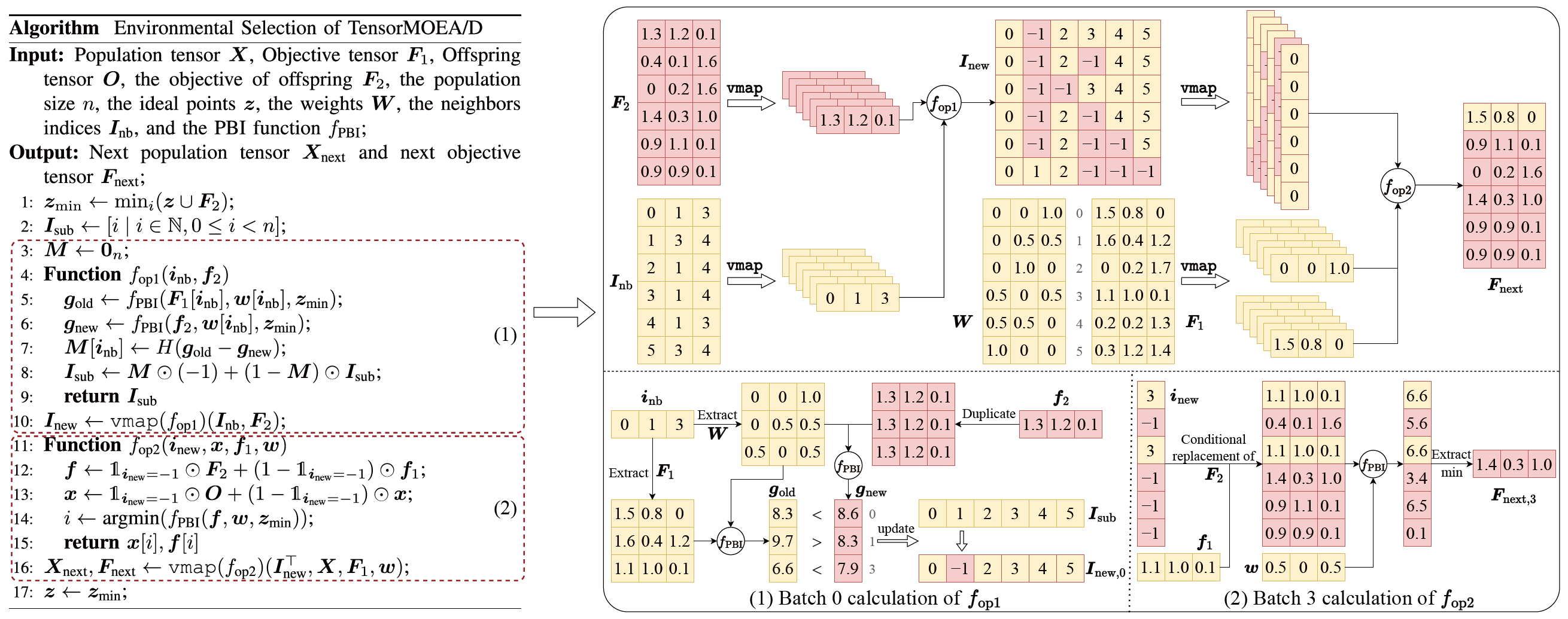
Рис. 3: Обзор отбора среды в алгоритме TensorMOEA/D. Слева: псевдокод алгоритма. Справа: тензорный поток данных модулей (1) и (2). Верхняя часть правого рисунка показывает общий тензорный поток данных для модулей (1) и (2), а нижняя часть представляет тензорный поток данных пакетных вычислений: модуль (1) слева и модуль (2) справа.
Для более полного понимания ценности тензоризации в EMO-алгоритмах её можно обобщить с трёх точек зрения. Во-первых, тензоризация обеспечивает прямое преобразование математических формулировок в эффективный код, сокращая разрыв между проектированием алгоритма и его реализацией. Например, Рис. 4 иллюстрирует, как тензоризованная процедура недоминируемой сортировки может быть напрямую переведена из псевдокода в код Python. Во-вторых, тензоризация значительно упрощает структуру кода, объединяя операции на уровне популяции в единое тензорное представление. Это снижает зависимость от циклов и условных операторов, тем самым улучшая читаемость и сопровождаемость кода. В-третьих, тензоризация повышает воспроизводимость алгоритмов. Её структурированное представление облегчает сравнительное тестирование и последовательное воспроизведение результатов.

Рис. 4: Бесшовное преобразование тензоризованной недоминируемой сортировки из псевдокода (слева) в код Python (справа).
Демонстрация производительности
Для оценки производительности GPU-ускоренных алгоритмов многокритериальной оптимизации команда EvoX систематически провела три категории экспериментов, сосредоточенных на вычислительном ускорении, производительности численной оптимизации и эффективности в задачах многокритериального управления роботами.
Производительность вычислительного ускорения:
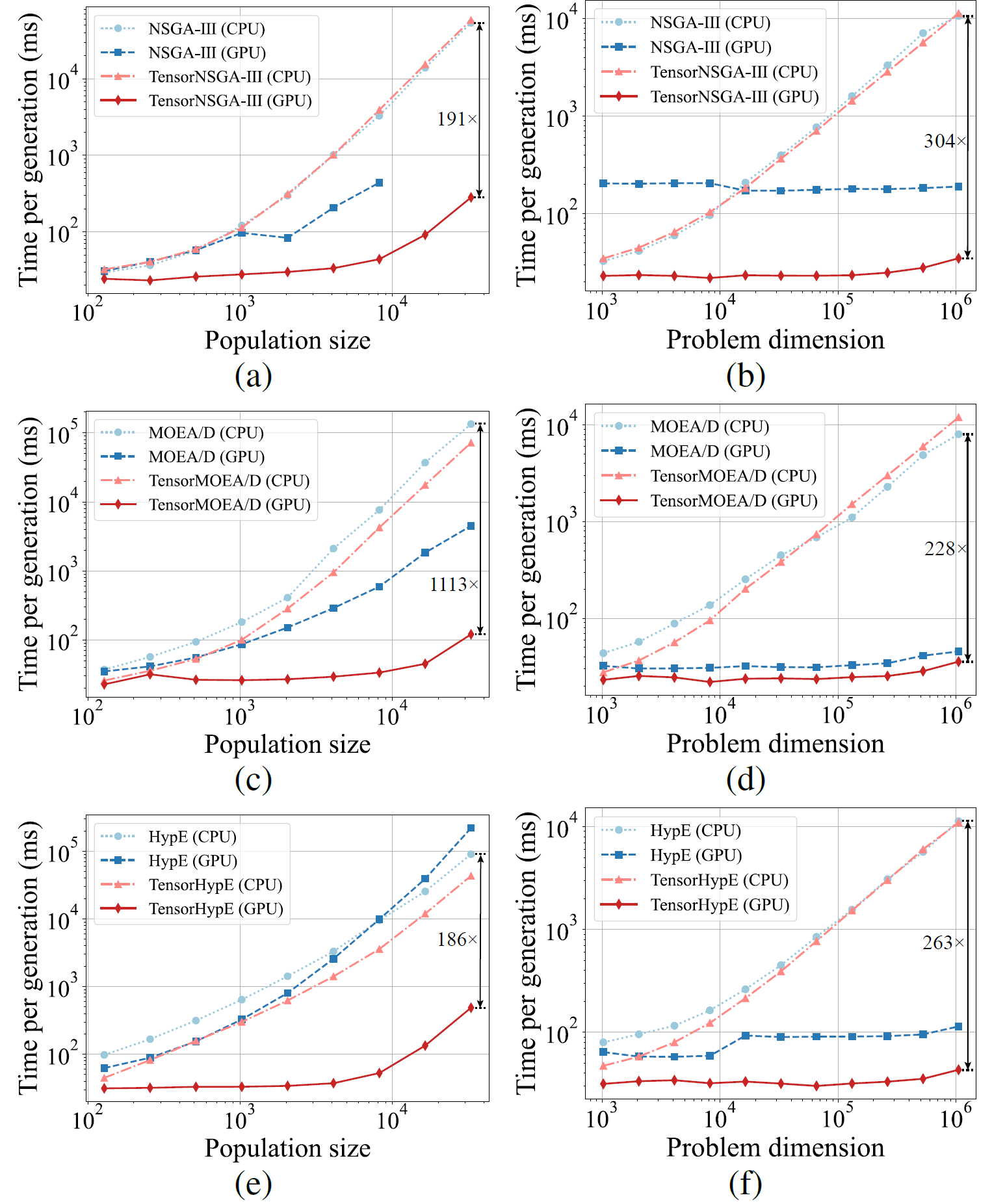
Рис. 5: Сравнительная производительность ускорения NSGA-III, MOEA/D и HypE с их тензоризованными аналогами на платформах CPU и GPU при различных размерах популяции и размерности задачи.
Экспериментальные результаты показывают, что TensorNSGA-III, TensorMOEA/D и TensorHypE достигают значительно более высокой скорости выполнения на GPU по сравнению с их нетензоризованными аналогами на CPU. По мере увеличения размера популяции и размерности задачи максимальное наблюдаемое ускорение достигает 1113 раз. Тензоризованные алгоритмы демонстрируют отличную масштабируемость и стабильность при обработке крупномасштабных вычислительных задач — их время выполнения увеличивается лишь незначительно, при этом сохраняя стабильно высокую производительность. Эти результаты подчёркивают существенные преимущества тензоризации для GPU-ускорения в многокритериальной оптимизации.
Производительность на наборе тестов LSMOP:
Таблица II: Статистические результаты (среднее и стандартное отклонение) IGD и времени выполнения (с) для нетензоризованных и тензоризованных EMO-алгоритмов на LSMOP1—LSMOP9. Все эксперименты проведены на GPU RTX 4090, лучшие результаты выделены.
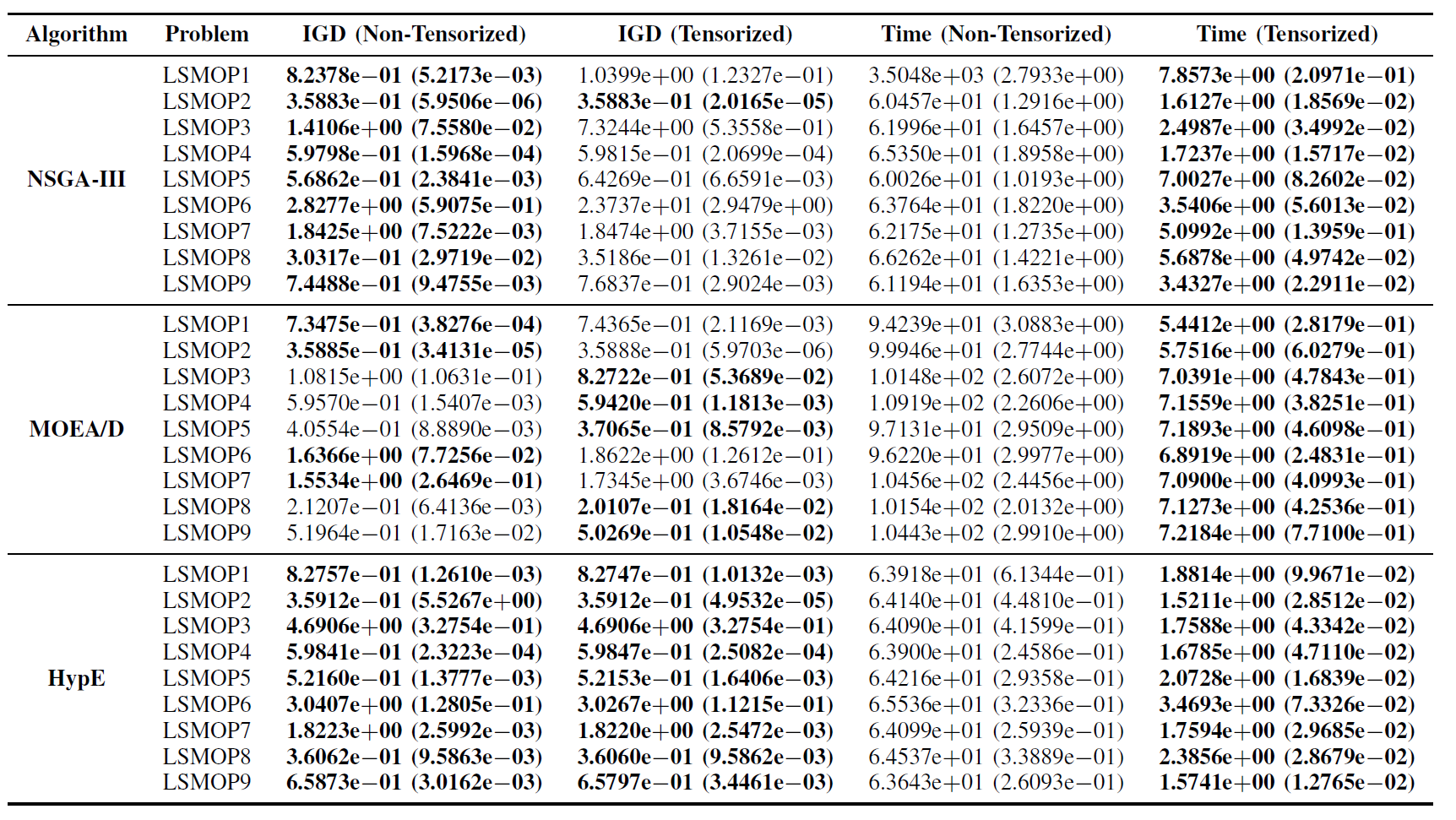
Экспериментальные результаты показывают, что GPU-ускоренные EMO-алгоритмы на основе тензоризованных представлений значительно повышают вычислительную эффективность, сохраняя, а в некоторых случаях даже превосходя точность оптимизации своих оригинальных аналогов.
Задачи многокритериального управления роботами:
Для всесторонней оценки практической производительности GPU-ускоренных EMO-алгоритмов команда разработала набор бенчмарков под названием MoRobtrol для многокритериального управления роботами. Задачи, включённые в этот набор, перечислены в Таблице III.
Таблица III: Обзор задач многокритериального управления роботами в предложенном наборе бенчмарков MoRobtrol
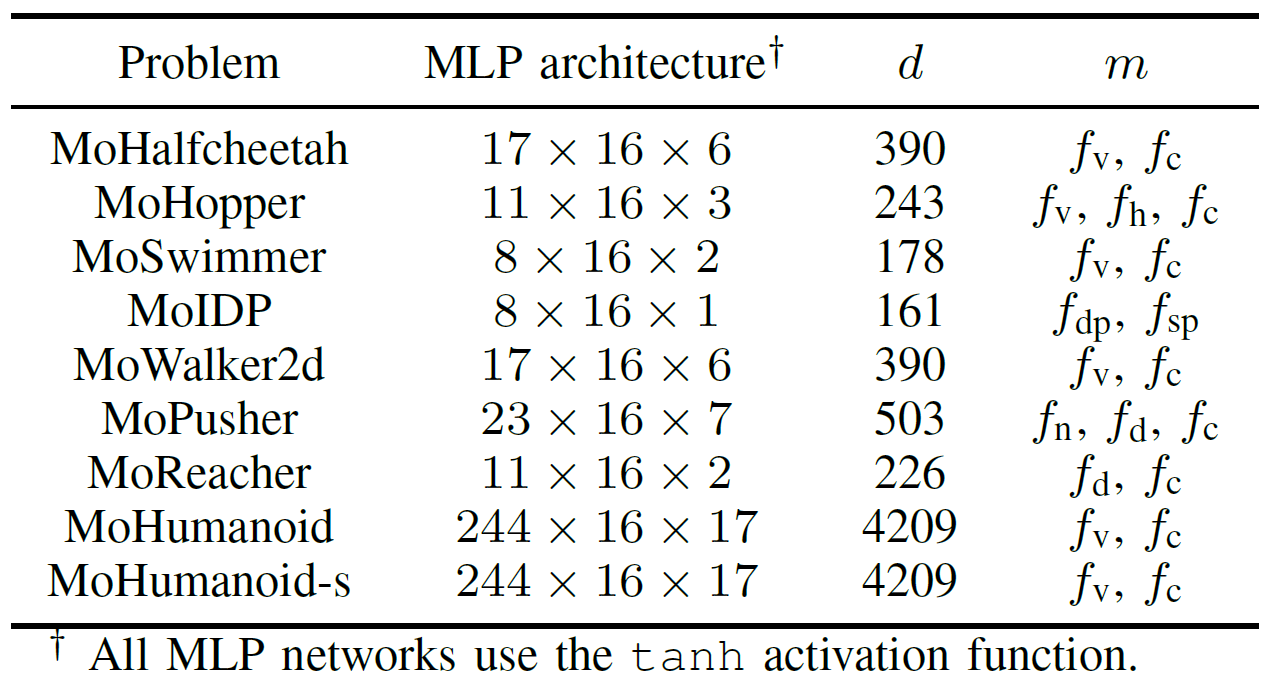
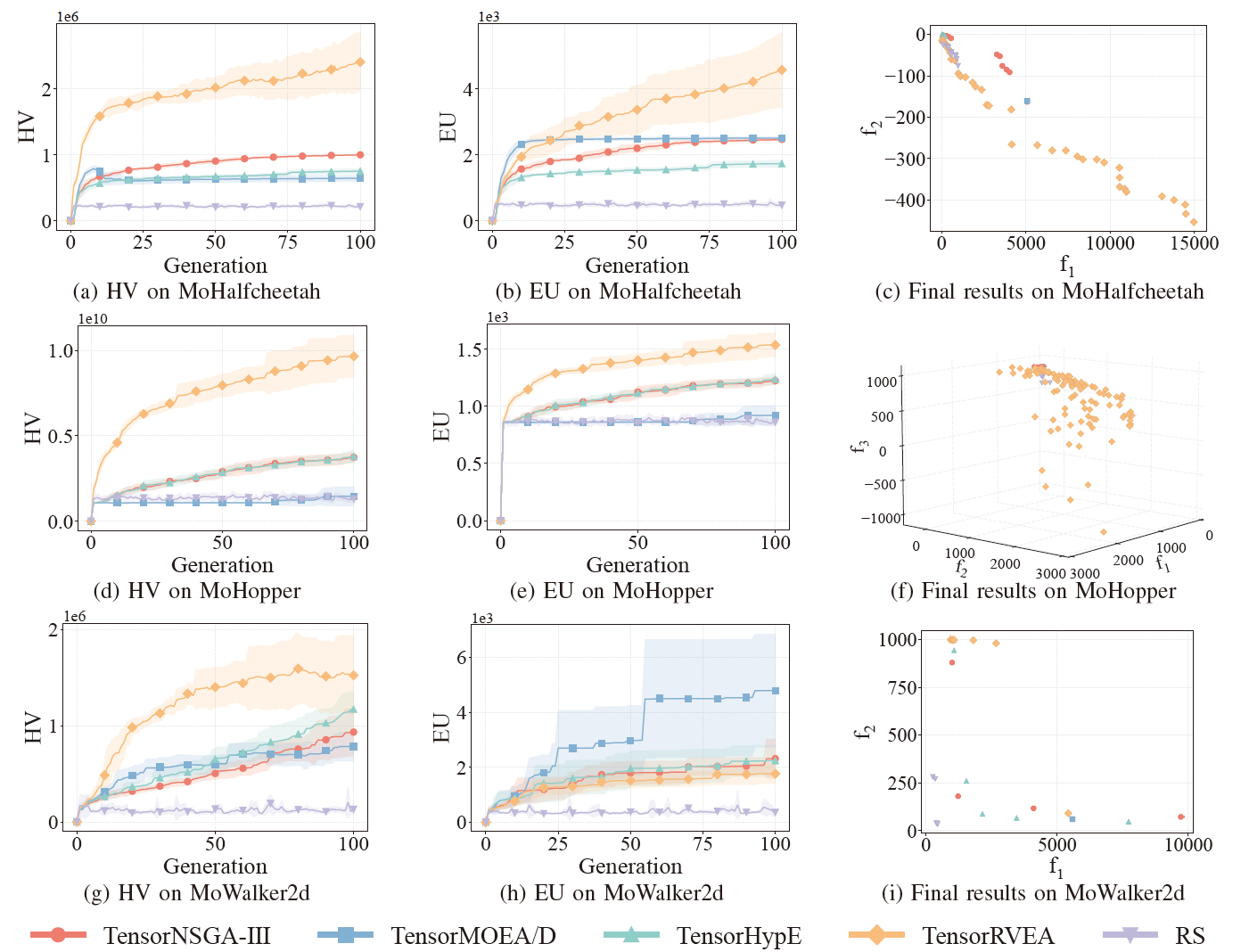
Рис. 6: Сравнительная производительность (HV, EU и визуализация финальных результатов) TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA и случайного поиска (RS) для различных задач: MoHalfcheetah (390D), MoHopper (243D) и MoWalker2d (390D). Примечание: более высокие значения всех метрик указывают на лучшую производительность.
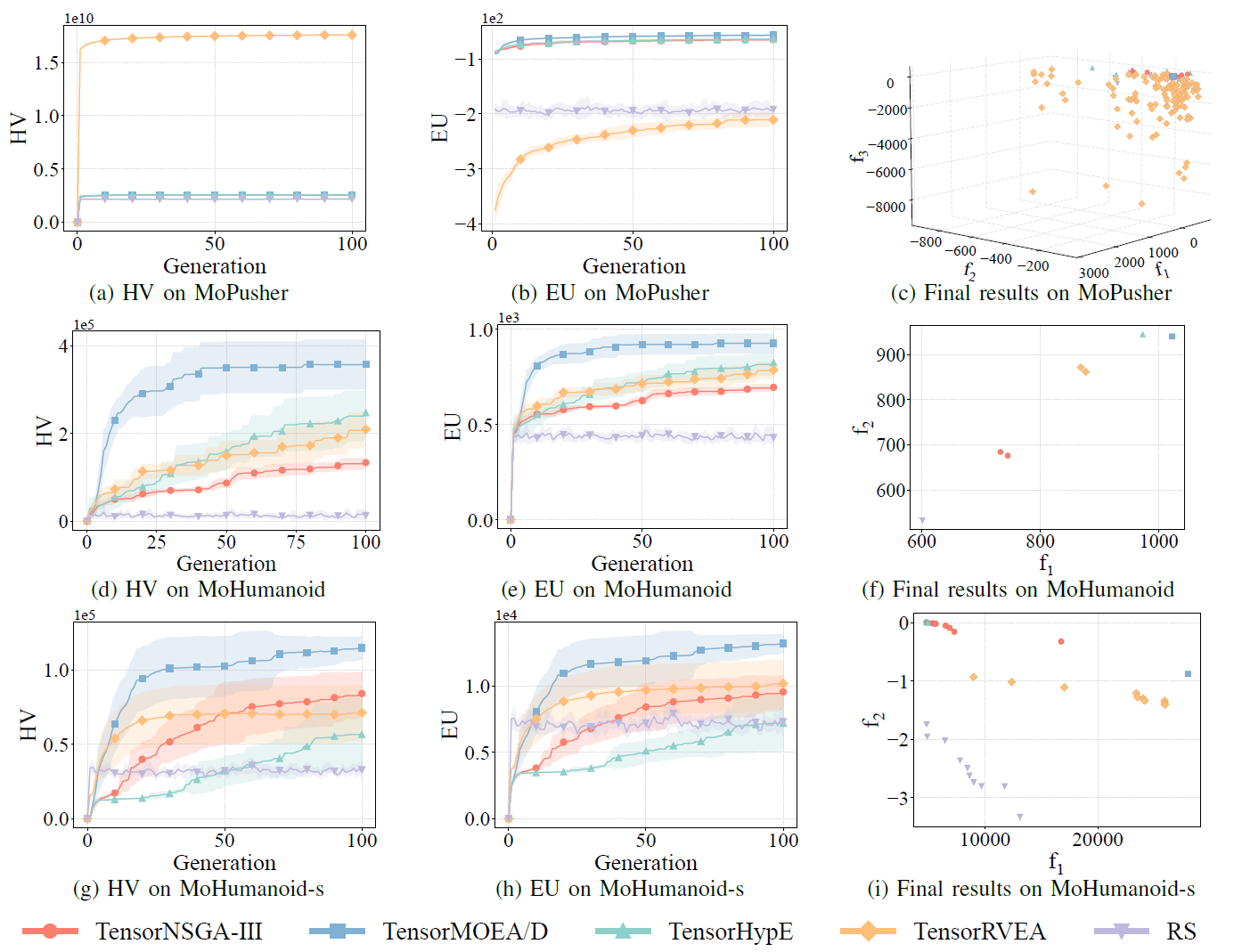
Рис. 7: Сравнительная производительность (HV, EU и визуализация финальных результатов) TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA и случайного поиска (RS) для различных задач: MoPusher (503D), MoHumanoid (4209D) и MoHumanoid-s (4209D). Примечание: более высокие значения всех метрик указывают на лучшую производительность.
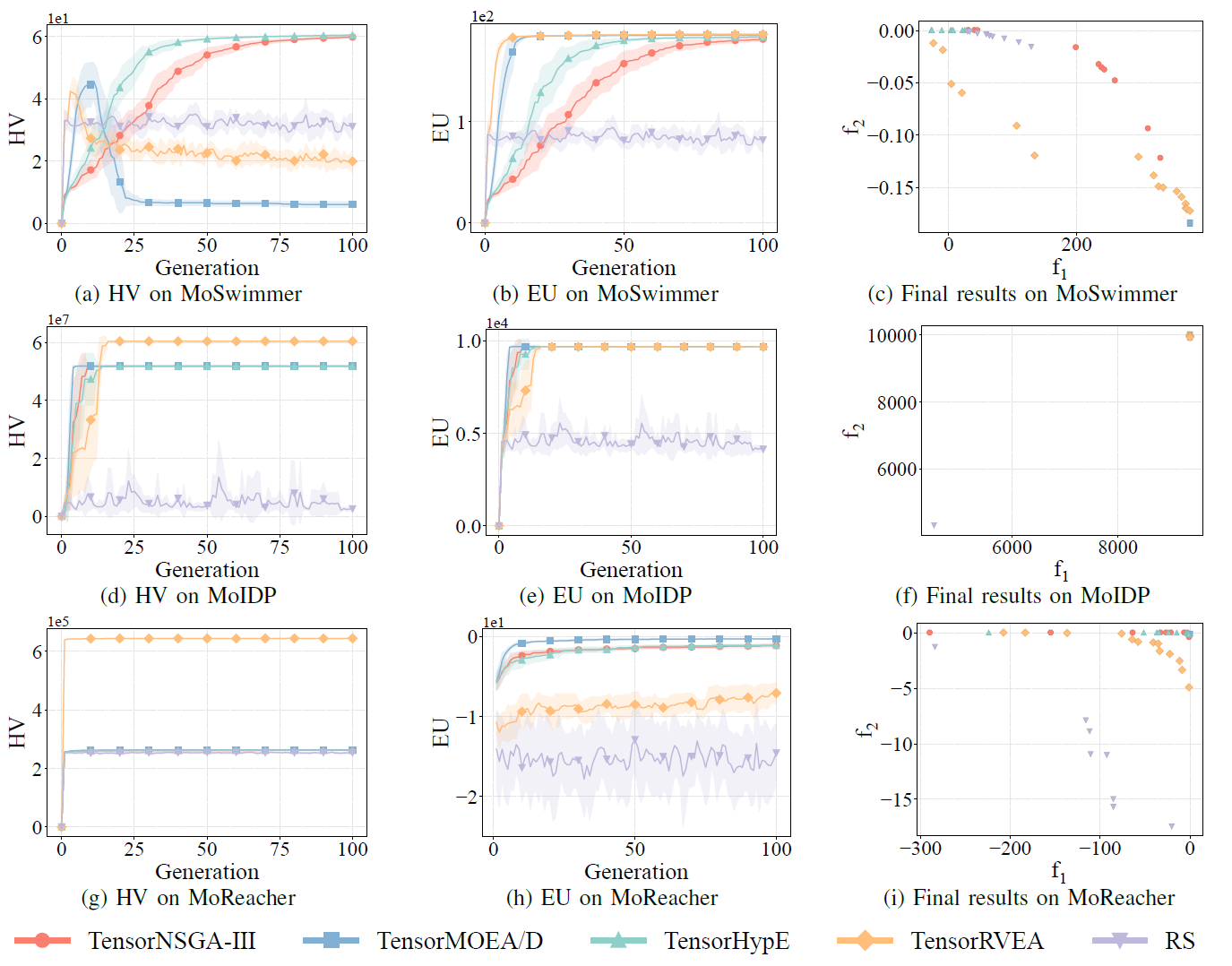
Рис. 8: Сравнительная производительность (HV, EU и визуализация финальных результатов) TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA и случайного поиска (RS) для различных задач: MoSwimmer (178D), MoIDP (161D) и MoReacher (226D). Примечание: более высокие значения всех метрик указывают на лучшую производительность.
В экспериментах сравнивалась производительность TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA и случайного поиска (RS) в рамках бенчмарка MoRobtrol. Результаты показывают, что TensorRVEA достиг лучшей общей производительности, получив наивысшие значения HV и продемонстрировав хорошее разнообразие решений в нескольких средах. TensorMOEA/D показал высокую адаптивность в крупномасштабных задачах, особенно отличаясь в согласованности предпочтений решений. TensorNSGA-III и TensorHypE показали схожую производительность и были конкурентоспособны в нескольких задачах. В целом тензоризованные алгоритмы на основе декомпозиции продемонстрировали превосходные преимущества при решении крупномасштабных и сложных задач.
Заключение и перспективы В данном исследовании предложена методология тензоризованного представления для преодоления ограничений традиционных EMO-алгоритмов на базе CPU в отношении вычислительной эффективности и масштабируемости. Подход был применён к нескольким представительным алгоритмам, включая NSGA-III, MOEA/D и HypE, достигнув значительного повышения производительности на GPU при сохранении качества решений. Для подтверждения практической применимости команда также разработала MoRobtrol — набор бенчмарков для многокритериального управления роботами, который переформулирует задачи управления роботами в средах физического моделирования как задачи многокритериальной оптимизации. Результаты демонстрируют потенциал тензоризованных алгоритмов в вычислительно интенсивных сценариях, таких как воплощённый интеллект. Хотя метод тензоризации существенно повысил эффективность алгоритмов, остаётся пространство для дальнейшего улучшения. Перспективные направления включают совершенствование ключевых операторов, таких как недоминируемая сортировка, разработку новых тензоризованных операций для мульти-GPU систем и интеграцию крупномасштабных данных и методов глубокого обучения для дальнейшего повышения производительности на крупномасштабных задачах оптимизации.
Открытый исходный код / Ресурсы сообщества
Статья:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
Вышестоящий проект (EvoX):
https://github.com/EMI-Group/evox
QQ-группа: 297969717

EvoMO построен на основе фреймворка EvoX. Если вы хотите узнать больше о EvoX, ознакомьтесь с официальной статьёй о EvoX 1.0, опубликованной в нашем публичном аккаунте WeChat.


