テンソル化による進化的多目的最適化
とGPU加速の橋渡し
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
工学設計やエネルギー管理などの分野における複雑な最適化ソリューションへの需要が継続的に高まる中、進化的多目的最適化(EMO)アルゴリズムは、多目的問題を解決する堅牢な能力により広く注目を集めています。しかし、最適化タスクの規模と複雑さが増大するにつれて、従来のCPUベースのEMOアルゴリズムは重大なパフォーマンスボトルネックに直面しています。
この制約に対処するため、EvoXチームはテンソル化手法を用いてEMOアルゴリズムをGPU上で並列化することを提案しました。この手法を活用して、いくつかのGPU加速EMOアルゴリズムの設計と実装に成功しました。さらに、チームはBrax物理エンジン上に構築された多目的ロボット制御のためのベンチマークスイートである**「MoRobtrol」**を開発し、GPU加速EMOアルゴリズムの性能を体系的に評価することを目指しています。
これらの研究成果に基づき、EvoXチームは高性能GPU加速EMOアルゴリズムライブラリであるEvoMOをリリースしました。対応するソースコードはGitHubで公開されています:https://github.com/EMl-Group/evomo
テンソル化手法
計算最適化の分野において、テンソルとはスカラー、ベクトル、行列、およびより高次のデータを表現できる多次元配列データ構造を指します。テンソル化とは、アルゴリズム内のデータ構造と演算をテンソル形式に変換するプロセスであり、アルゴリズムがGPUの並列計算能力を最大限に活用できるようにします。
EMOアルゴリズムにおいて、すべての主要なデータ構造はテンソル化された形式で表現できます。集団内の個体は解テンソルXで表現でき、各行ベクトルが1つの個体に対応します。目的関数値は目的テンソルFを形成します。さらに、参照ベクトルや重みベクトルなどの補助データ構造は、それぞれテンソルRとWとして表現できます。この統一的なテンソル表現により、表現レベルでの集団レベルの操作が可能となり、大規模並列計算の堅固な基盤を築きます。
EMOアルゴリズム操作のテンソル化は計算効率の向上に不可欠であり、基本テンソル演算と制御フローのテンソル化の2層に分けることができます。基本テンソル演算はEMOアルゴリズムのテンソル化実装の中核を構成し、表Iに詳述されています。
表I:基本テンソル演算

制御フローのテンソル化は、従来のループや条件分岐ロジックを並列化可能なテンソル演算に置き換えます。例えば、for/whileループはブロードキャスティングメカニズムやvmapなどの高階関数を使用してバッチ演算に変換できます。同様に、if-else条件分岐はマスキング技術で置き換えることができ、論理条件をブールテンソルとしてエンコードすることで、異なる計算パス間の柔軟な切り替えが可能になります。
従来のEMOアルゴリズム実装と比較して、テンソル化アプローチには大きな利点があります。第一に、多次元データを自然に扱えるより高い柔軟性を提供しますが、従来の手法は二次元行列演算に制限されることが多いです。第二に、テンソル化は並列実行を通じて計算効率を大幅に向上させ、明示的なループや条件分岐に伴うオーバーヘッドを回避します。最後に、コード構造を簡素化し、より簡潔で保守しやすいプログラムを実現します。
図1に示すように、例えば、パレート支配チェックの従来の実装はネストされたループに依存して要素ごとの比較を行います。これに対し、テンソル化バージョンはブロードキャスティングとマスキング演算を通じて同じ機能を実現し、並列評価を可能にします。これにより、コードの複雑さが軽減されるだけでなく、実行時パフォーマンスも劇的に向上します。

図1:パレート支配検出の従来実装とテンソルベース実装の比較。
より深い視点から見ると、テンソル化はGPU加速に適しています。GPUは多数の並列コアを持ち、そのSIMT(Single-Instruction Multiple-Thread)アーキテクチャはテンソル計算と自然に整合し、特に行列演算に優れています。NVIDIAのTensor Coresなどの専用ハードウェアは、テンソル演算のスループットをさらに向上させます。一般的に、高い並列性を示し、独立した計算タスクを含み、条件分岐が最小限のアルゴリズムは、テンソル化により適しています。MOEA/Dのように逐次的な依存関係を含むアルゴリズムでは、固有の構造が直接的なテンソル化に課題をもたらします。しかし、構造的なリファクタリングと重要な計算の分離を通じて、効果的な並列加速を達成することは依然として可能です。
アルゴリズムテンソル化の適用例
テンソル化表現手法に基づき、EvoXチームは3つの古典的なEMOアルゴリズムのテンソル化バージョンを設計・実装しました:支配ベースのNSGA-III、分解ベースのMOEA/D、指標ベースのHypEです。以下のセクションでは、MOEA/Dを例として詳細に説明します。NSGA-IIIとHypEのテンソル化実装は参照論文に記載されています。
図2に示すように、従来のMOEA/Dは多目的問題を複数のサブ問題に分解し、それぞれを独立に最適化します。アルゴリズムは4つのコアステップで構成されます:交叉と突然変異、適応度評価、理想点の更新、近傍更新。これらのステップは単一ループ内で各個体に対して逐次的に実行されます。この逐次処理は、大規模集団を扱う際に大きな計算オーバーヘッドをもたらします。各個体がすべてのステップを順番に完了する必要があるため、GPU加速の潜在的な利点が制限されます。特に、近傍更新は個体間の相互作用に依存しており、並列化をさらに複雑にしています。

図2:MOEA/Dの擬似コード
従来のMOEA/Dにおける逐次依存性の問題に対処するため、チームは環境選択の内部ループ内にテンソル化表現手法を導入しました。交叉と突然変異、適応度評価、理想点の更新、近傍更新を分離し、これらのコンポーネントを独立した操作として扱うことで、すべての個体の並列処理が可能となり、TensorMOEA/Dと呼ばれるテンソル化MOEA/Dアルゴリズムの構築につながりました。このアルゴリズムでは、環境選択は2つの主要な段階に分けられます:比較と集団更新、およびエリート解の選択。これら2つの段階は主にvmap演算の2回の適用を通じてテンソル化されます。詳細なプロセスは図3に示されています。
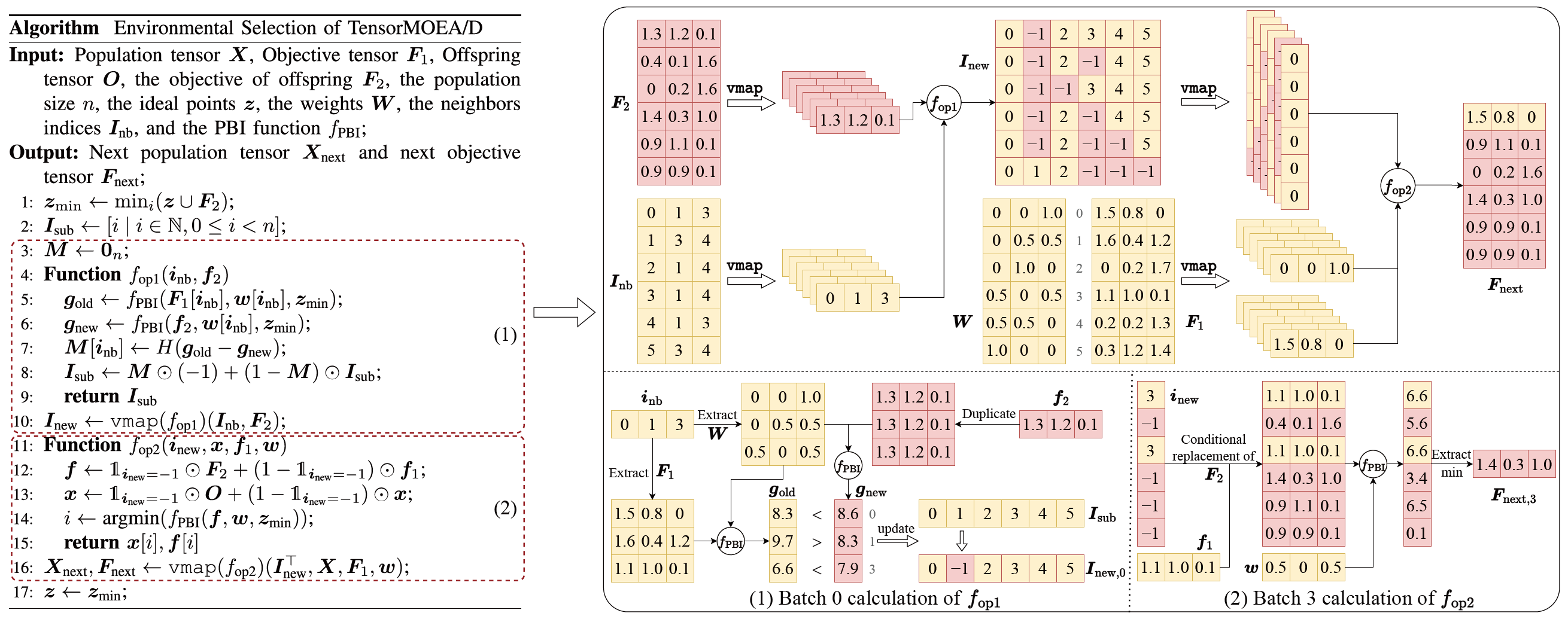
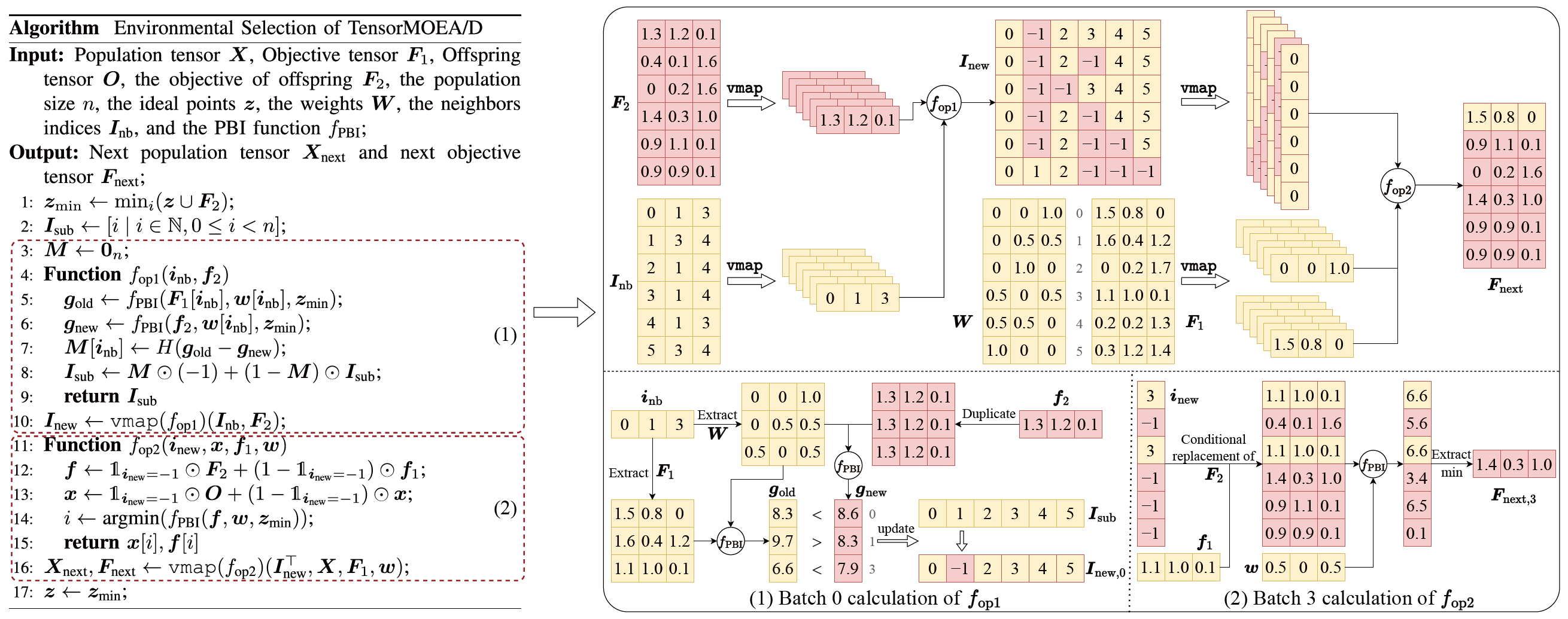
図3:TensorMOEA/Dアルゴリズムにおける環境選択の概要。左:アルゴリズムの擬似コード。右:モジュール(1)とモジュール(2)のテンソルデータフロー。右図の上部はモジュール(1)と(2)の全体的なテンソルデータフローを示し、下部はバッチ計算テンソルデータフローを示しています(左がモジュール(1)、右がモジュール(2))。
EMOアルゴリズムにおけるテンソル化の価値をより包括的に理解するために、3つの観点から要約できます。第一に、テンソル化は数学的定式化から効率的なコードへの直接的な変換を可能にし、アルゴリズム設計と実装のギャップを縮小します。例えば、図4はテンソル化された非支配ソーティング手順が擬似コードからPythonコードに直接変換できることを示しています。第二に、テンソル化は集団レベルの操作を単一のテンソル表現に統一することでコード構造を大幅に簡素化します。これにより、ループや条件文への依存が減少し、コードの可読性と保守性が向上します。第三に、テンソル化はアルゴリズムの再現性を向上させます。その構造化された表現は、比較テストと結果の一貫した再現を容易にします。

図4:テンソル化された非支配ソーティングの擬似コード(左)からPythonコード(右)へのシームレスな変換。
性能実証
GPU加速多目的最適化アルゴリズムの性能を評価するため、EvoXチームは計算加速、数値最適化性能、多目的ロボット制御タスクにおける有効性に焦点を当てた3カテゴリの実験を体系的に実施しました。
計算加速性能:
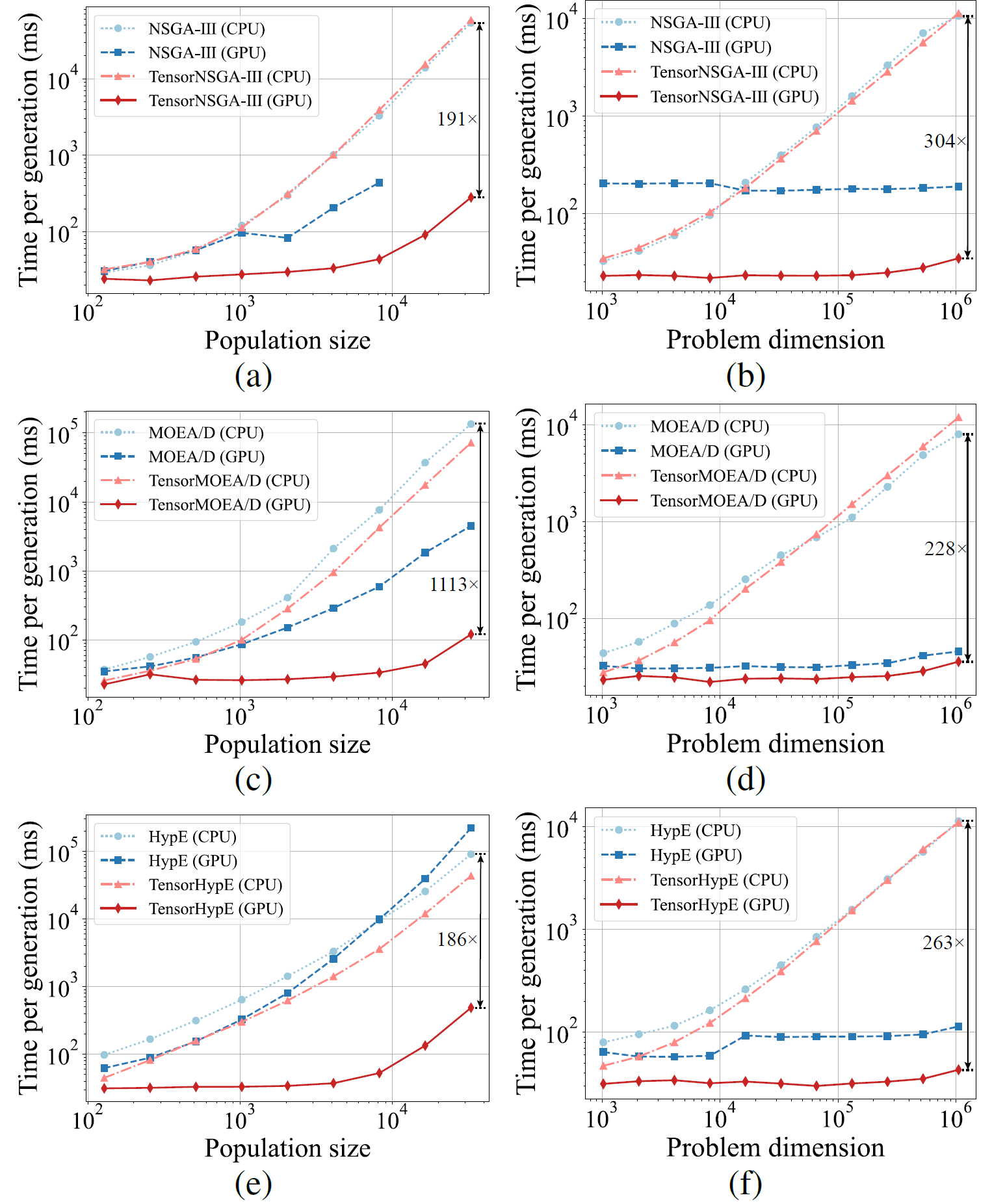
図5:さまざまな集団サイズと問題次元にわたるCPUおよびGPUプラットフォーム上でのNSGA-III、MOEA/D、HypEとそのテンソル化版の比較加速性能。
実験結果は、TensorNSGA-III、TensorMOEA/D、TensorHypEが、非テンソル化CPUベースの対応版と比較して、GPU上で大幅に高い実行速度を達成することを示しています。集団サイズと問題次元が増加するにつれて、観測された最大スピードアップは1113倍に達します。テンソル化アルゴリズムは、大規模計算タスクを処理する際に優れたスケーラビリティと安定性を示し、実行時間はわずかに増加するのみで、一貫して高いパフォーマンスを維持しています。これらの知見は、多目的最適化におけるGPU加速のためのテンソル化の大きな利点を強調しています。
LSMOPテストスイートにおける性能:
表II:LSMOP1—LSMOP9における非テンソル化およびテンソル化EMOアルゴリズムのIGDと実行時間(秒)の統計結果(平均と標準偏差)。すべての実験はRTX 4090 GPU上で実施され、最良の結果が強調表示されています。
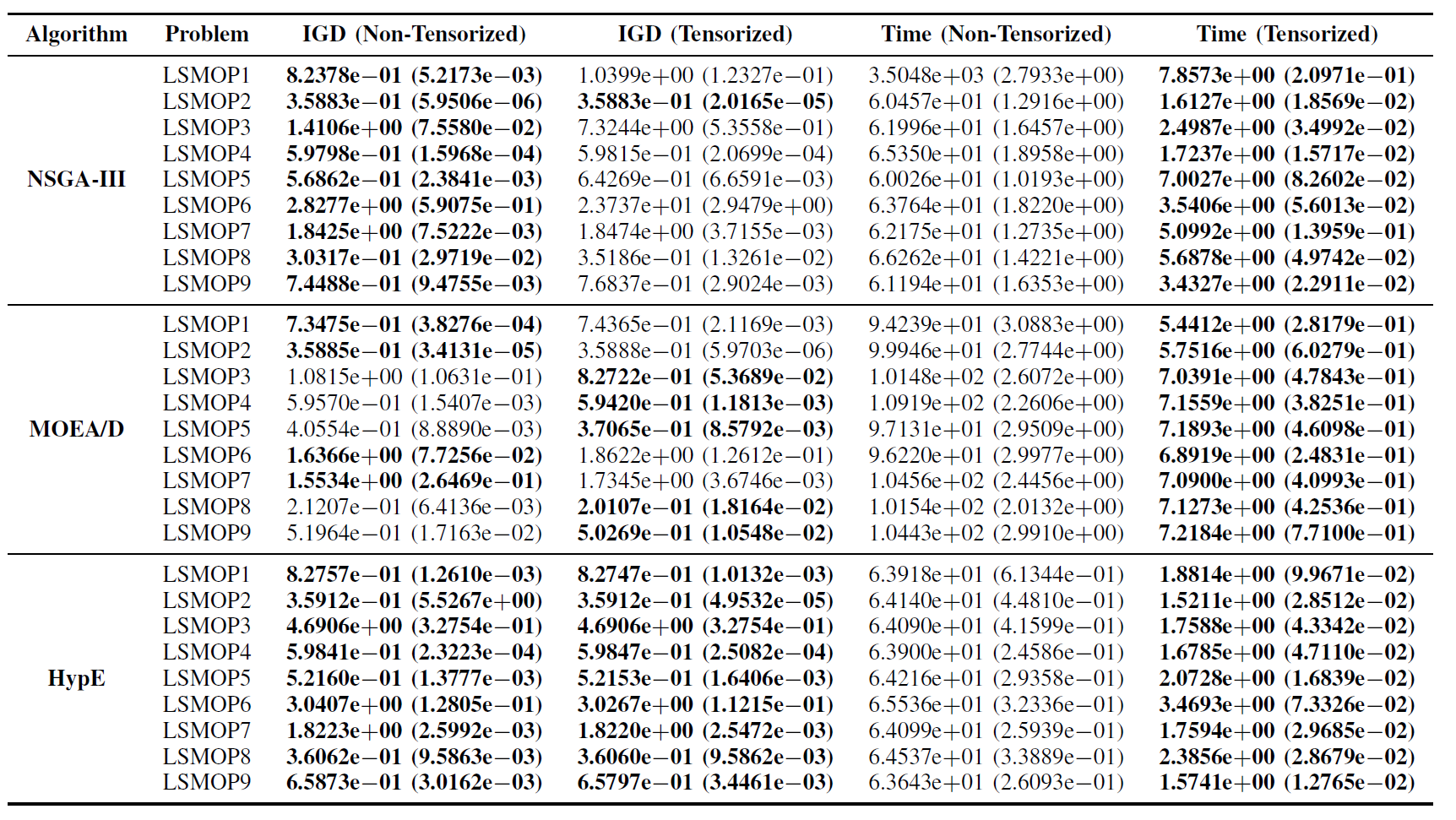
実験結果は、テンソル化表現に基づくGPU加速EMOアルゴリズムが、元の対応版の最適化精度を維持しながら、場合によってはそれを上回りつつ、計算効率を大幅に改善することを示しています。
多目的ロボット制御タスク:
GPU加速EMOアルゴリズムの実用的な性能を包括的に評価するため、チームは多目的ロボット制御のためのMoRobtrolというベンチマークスイートを開発しました。このスイートに含まれるタスクは表IIIに記載されています。
表III:提案されたMoRobtrolベンチマークテストスイートにおける多目的ロボット制御問題の概要
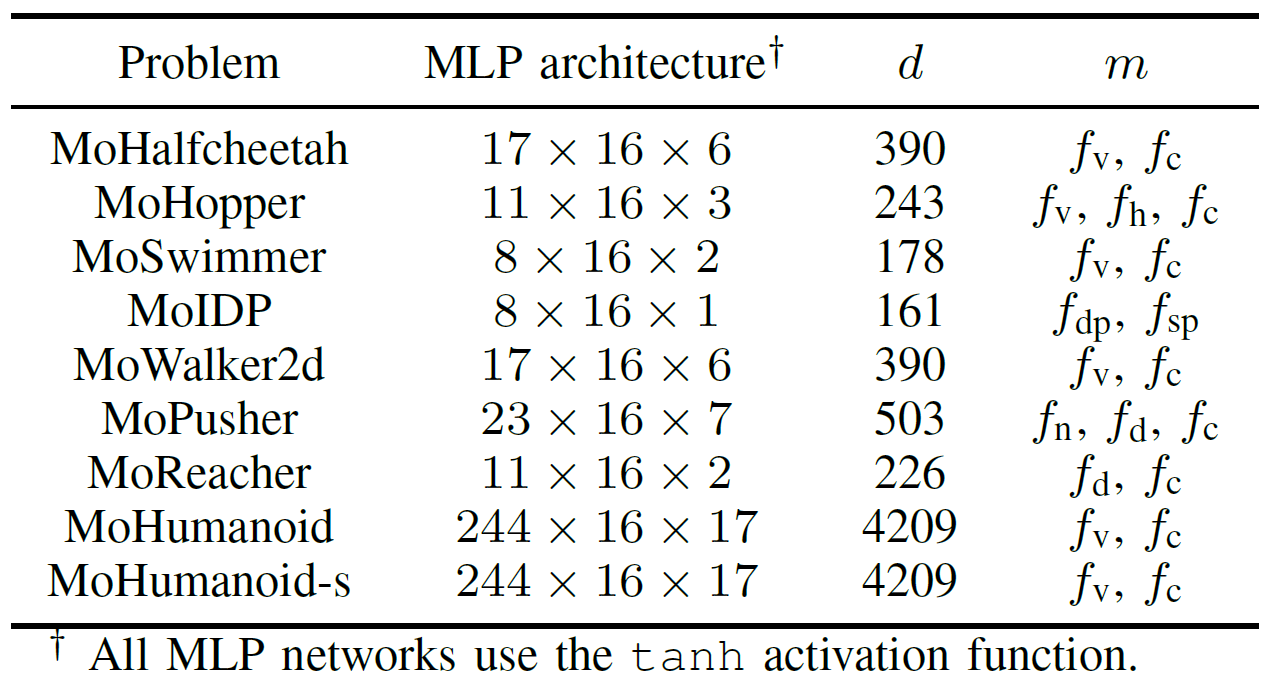
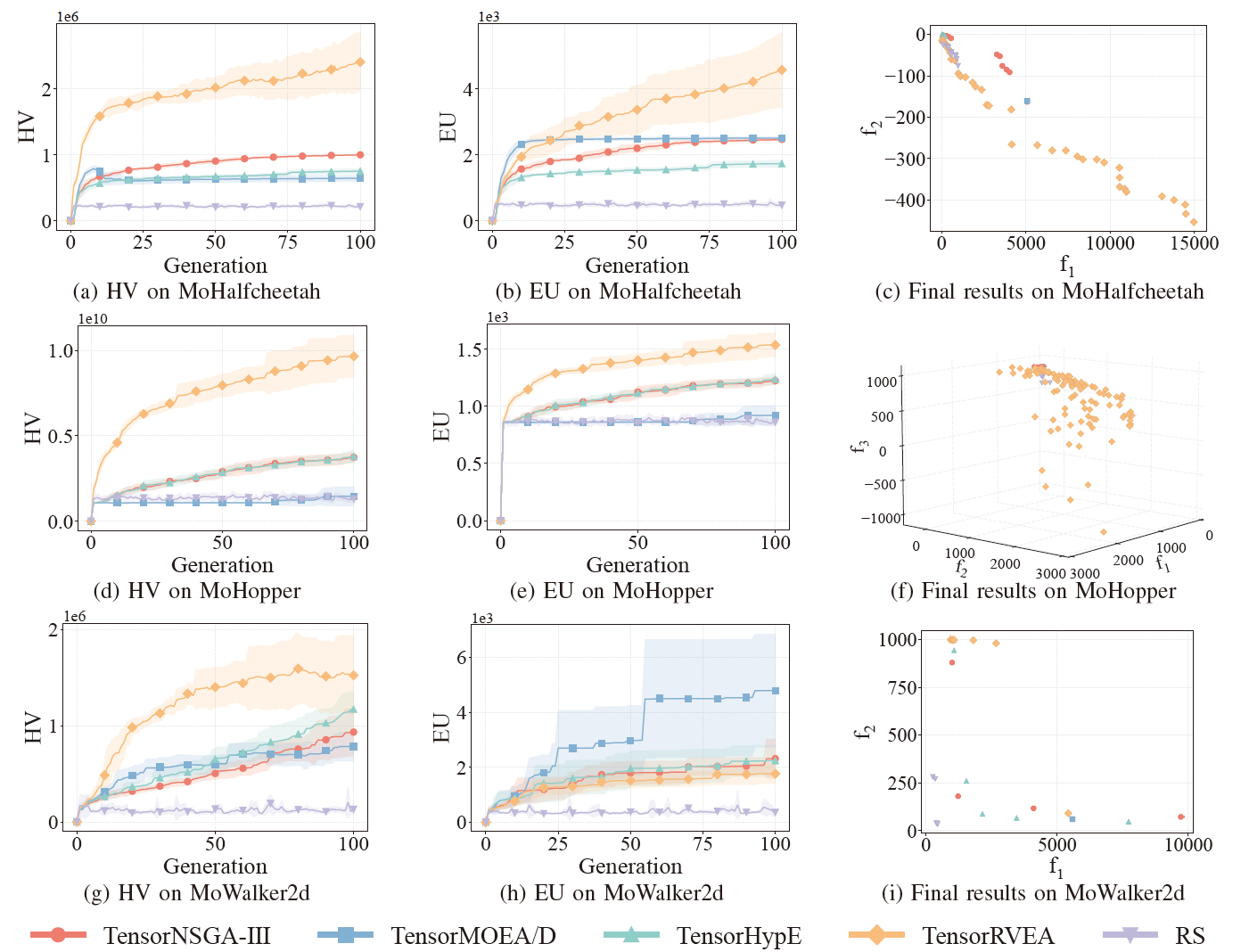
図6:さまざまな問題にわたるTensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA、ランダムサーチ(RS)の比較性能(HV、EU、最終結果の可視化):MoHalfcheetah(390D)、MoHopper(243D)、MoWalker2d(390D)。注:すべての指標において値が高いほど性能が良いことを示します。
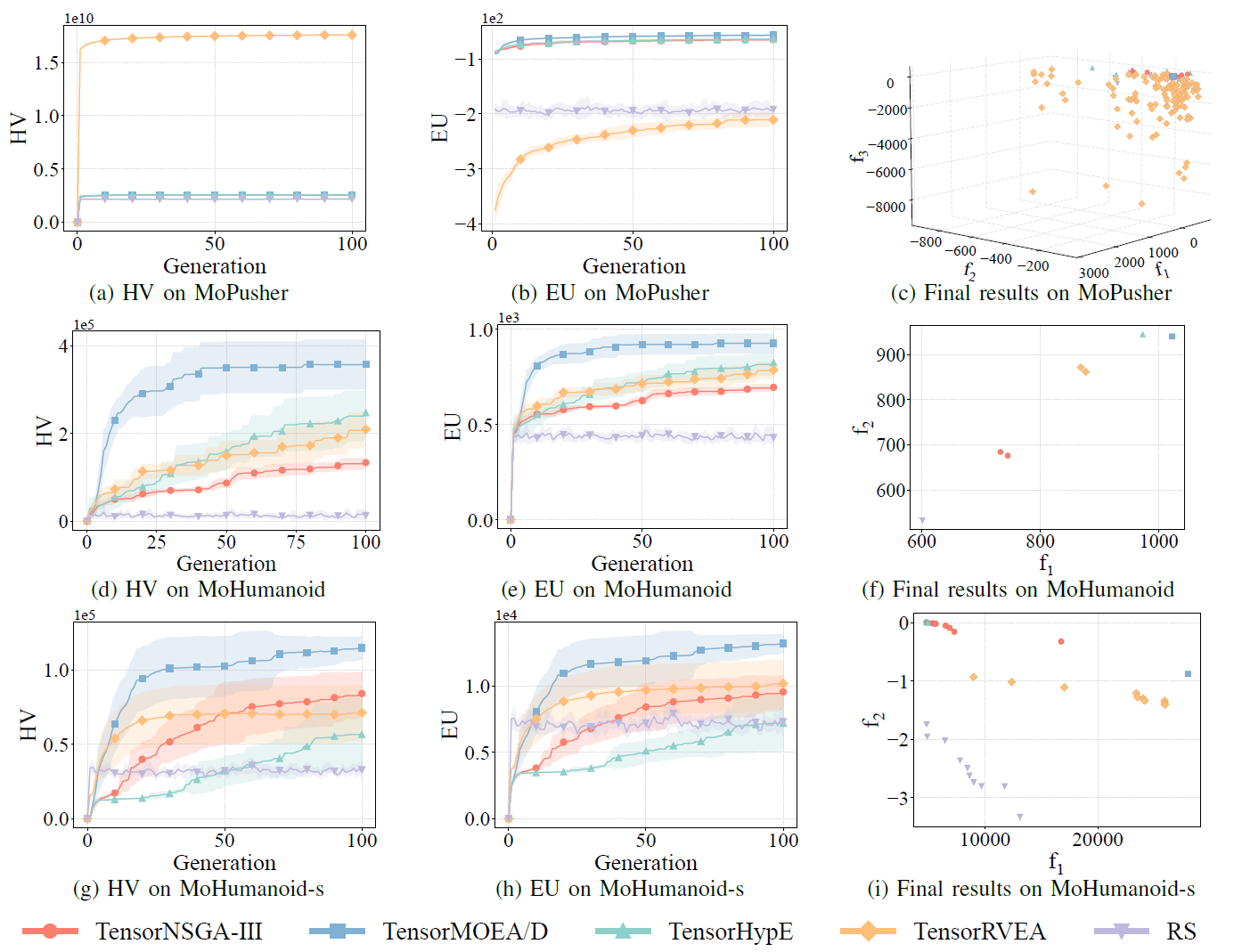
図7:さまざまな問題にわたるTensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA、ランダムサーチ(RS)の比較性能(HV、EU、最終結果の可視化):MoPusher(503D)、MoHumanoid(4209D)、MoHumanoid-s(4209D)。注:すべての指標において値が高いほど性能が良いことを示します。
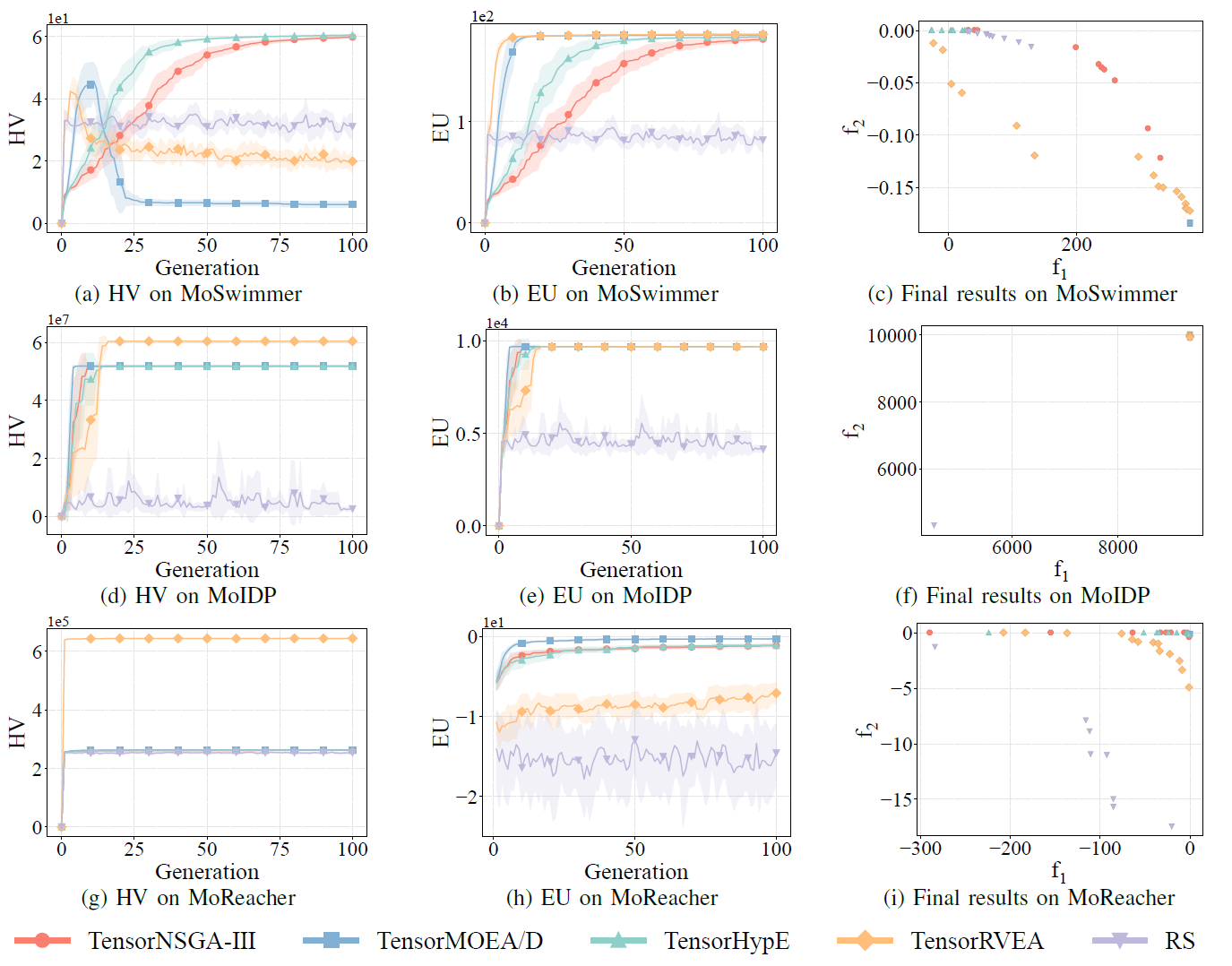
図8:さまざまな問題にわたるTensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA、ランダムサーチ(RS)の比較性能(HV、EU、最終結果の可視化):MoSwimmer(178D)、MoIDP(161D)、MoReacher(226D)。注:すべての指標において値が高いほど性能が良いことを示します。
実験では、MoRobtrolベンチマーク内でTensorNSGA-III、TensorMOEA/D、TensorHypE、TensorRVEA、ランダムサーチ(RS)の性能を比較しました。結果は、TensorRVEAが最も優れた総合性能を達成し、最高のHV値を獲得し、複数の環境で良好な解の多様性を示したことを示しています。TensorMOEA/Dは大規模タスクにおいて強い適応性を示し、特に解の選好一貫性に優れていました。TensorNSGA-IIIとTensorHypEは同様の性能を示し、いくつかのタスクで競争力がありました。全体として、テンソル化された分解ベースのアルゴリズムは、大規模で複雑な問題の解決において優れた利点を示しました。
結論と今後の課題 本研究は、従来のCPUベースのEMOアルゴリズムにおける計算効率とスケーラビリティの制約に対処するため、テンソル化表現手法を提案しています。このアプローチはNSGA-III、MOEA/D、HypEを含むいくつかの代表的なアルゴリズムに適用され、解の品質を維持しながらGPU上で大幅な性能向上を達成しました。その実用的な適用可能性を検証するため、チームは物理シミュレーション環境におけるロボット制御タスクを多目的最適化問題として再定式化した多目的ロボット制御ベンチマークスイートMoRobtrolも開発しました。結果は、身体知能などの計算集約的なシナリオにおけるテンソル化アルゴリズムの可能性を示しています。テンソル化手法はアルゴリズムの効率を大幅に改善しましたが、さらなる向上の余地があります。今後の方向性には、非支配ソーティングなどのコアオペレータの改善、マルチGPUシステム向けの新しいテンソル化演算の設計、大規模データと深層学習技術の統合による大規模最適化問題のさらなる性能向上が含まれます。
オープンソースコード / コミュニティリソース
論文:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
上流プロジェクト (EvoX):
https://github.com/EMI-Group/evox
QQグループ: 297969717

EvoMOはEvoXフレームワーク上に構築されています。EvoXについてもっと知りたい方は、WeChat公式アカウントで公開されたEvoX 1.0に関する公式記事をぜひご覧ください。


