Collegare l’ottimizzazione multi-obiettivo evolutiva
e l’accelerazione GPU tramite tensorizzazione
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
Con la continua crescita della domanda di soluzioni di ottimizzazione complesse in domini come la progettazione ingegneristica e la gestione energetica, gli algoritmi di ottimizzazione multi-obiettivo evolutiva (EMO) hanno attirato un’ampia attenzione grazie alle loro robuste capacita nella risoluzione di problemi multi-obiettivo. Tuttavia, con l’aumento della scala e della complessita dei compiti di ottimizzazione, gli algoritmi EMO tradizionali basati su CPU incontrano significativi colli di bottiglia nelle prestazioni.
Per affrontare questa limitazione, il team EvoX ha proposto di parallelizzare gli algoritmi EMO su GPU tramite la metodologia di tensorizzazione. Sfruttando questo metodo, hanno progettato e implementato con successo diversi algoritmi EMO accelerati da GPU. Inoltre, il team ha sviluppato “MoRobtrol”, una suite di benchmark per il controllo robotico multi-obiettivo costruita sul motore fisico Brax, volta a valutare sistematicamente le prestazioni degli algoritmi EMO accelerati da GPU.
Sulla base di questi progressi nella ricerca, il team EvoX ha rilasciato EvoMO, una libreria di algoritmi EMO accelerati da GPU ad alte prestazioni. Il codice sorgente corrispondente e disponibile pubblicamente su GitHub: https://github.com/EMl-Group/evomo
Metodologia di tensorizzazione
Nel campo dell’ottimizzazione computazionale, un tensore si riferisce a una struttura dati di array multidimensionale capace di rappresentare scalari, vettori, matrici e dati di ordine superiore. La tensorizzazione e il processo di conversione delle strutture dati e delle operazioni all’interno di un algoritmo in forma tensoriale, consentendo all’algoritmo di sfruttare appieno le capacita di calcolo parallelo delle GPU.
Negli algoritmi EMO, tutte le strutture dati chiave possono essere espresse in formato tensorizzato. Gli individui in una popolazione possono essere rappresentati da un tensore di soluzioni X, dove ogni vettore riga corrisponde a un individuo. I valori della funzione obiettivo formano un tensore obiettivo F. Inoltre, strutture dati ausiliarie come i vettori di riferimento e i vettori peso possono essere espressi come tensori R e W, rispettivamente. Questa rappresentazione tensoriale unificata consente operazioni a livello di popolazione al livello della rappresentazione, ponendo una solida base per il calcolo parallelo su larga scala.
La tensorizzazione delle operazioni degli algoritmi EMO e cruciale per migliorare l’efficienza computazionale e puo essere suddivisa in due livelli: operazioni tensoriali di base e tensorizzazione del flusso di controllo. Le operazioni tensoriali di base costituiscono il nucleo dell’implementazione tensorizzata degli algoritmi EMO, come dettagliato nella Tabella I.
Tabella I: Operazioni tensoriali di base

La tensorizzazione del flusso di controllo sostituisce la logica tradizionale di cicli e condizioni con operazioni tensoriali parallelizzabili. Ad esempio, i cicli for/while possono essere trasformati in operazioni batch utilizzando meccanismi di broadcasting o funzioni di ordine superiore come vmap. Analogamente, i condizionali if-else possono essere sostituiti da tecniche di masking, dove le condizioni logiche sono codificate come tensori booleani, consentendo il passaggio flessibile tra diversi percorsi di calcolo.
Rispetto alle implementazioni tradizionali degli algoritmi EMO, l’approccio di tensorizzazione offre vantaggi significativi. In primo luogo, fornisce una maggiore flessibilita, gestendo naturalmente dati multidimensionali, mentre i metodi convenzionali sono spesso limitati a operazioni su matrici bidimensionali. In secondo luogo, la tensorizzazione migliora significativamente l’efficienza computazionale attraverso l’esecuzione parallela, evitando l’overhead associato a cicli espliciti e rami condizionali. Infine, semplifica la struttura del codice, risultando in programmi piu concisi e manutenibili.
Come illustrato nella Fig. 1, ad esempio, l’implementazione tradizionale del controllo della dominanza di Pareto si basa su cicli annidati per eseguire confronti elemento per elemento. Al contrario, la versione tensorizzata raggiunge la stessa funzionalita attraverso operazioni di broadcasting e masking, consentendo la valutazione parallela. Questo non solo riduce la complessita del codice, ma migliora drasticamente le prestazioni a runtime.

Fig.1: Confronto tra implementazioni convenzionali e basate su tensori del rilevamento della dominanza di Pareto.
Da una prospettiva piu profonda, la tensorizzazione e particolarmente adatta all’accelerazione GPU perche le GPU possiedono un gran numero di core paralleli, e la loro architettura single-instruction multiple-thread (SIMT) si allinea naturalmente con i calcoli tensoriali, eccellendo in particolare nelle operazioni matriciali. Hardware dedicato come i Tensor Core di NVIDIA migliora ulteriormente il throughput delle operazioni tensoriali. In generale, gli algoritmi che presentano un alto parallelismo, contengono compiti computazionali indipendenti e hanno un minimo di ramificazioni condizionali sono piu adatti alla tensorizzazione. Per algoritmi come MOEA/D, che coinvolgono dipendenze sequenziali, la struttura intrinseca pone sfide alla tensorizzazione diretta. Tuttavia, attraverso la ristrutturazione e il disaccoppiamento dei calcoli critici, e comunque possibile ottenere un’accelerazione parallela efficace.
Esempio applicativo della tensorizzazione degli algoritmi
Sulla base della metodologia di rappresentazione tensorizzata, il team EvoX ha progettato e implementato versioni tensorizzate di tre algoritmi EMO classici: NSGA-III basato sulla dominanza, MOEA/D basato sulla decomposizione e HypE basato sugli indicatori. La sezione seguente fornisce una spiegazione dettagliata utilizzando MOEA/D come esempio. Le implementazioni tensorizzate di NSGA-III e HypE possono essere trovate nell’articolo di riferimento.
Come illustrato nella Fig. 2, il tradizionale MOEA/D decompone un problema multi-obiettivo in molteplici sottoproblemi, ciascuno dei quali viene ottimizzato indipendentemente. L’algoritmo comprende quattro passaggi fondamentali: crossover e mutazione, valutazione della fitness, aggiornamento del punto ideale e aggiornamento del vicinato. Questi passaggi vengono eseguiti sequenzialmente per ogni individuo all’interno di un singolo ciclo. Questa elaborazione sequenziale comporta un overhead computazionale sostanziale quando si gestiscono grandi popolazioni, poiche ogni individuo deve completare tutti i passaggi in ordine, limitando i potenziali benefici dell’accelerazione GPU. In particolare, l’aggiornamento del vicinato si basa sulle interazioni tra individui, il che complica ulteriormente la parallelizzazione.

Fig.2: Pseudocodice di MOEA/D
Per affrontare il problema delle dipendenze sequenziali nel tradizionale MOEA/D, il team ha introdotto un metodo di rappresentazione tensorizzata all’interno del ciclo interno della selezione ambientale. Disaccoppiando crossover e mutazione, valutazione della fitness, aggiornamento del punto ideale e aggiornamento del vicinato, questi componenti vengono trattati come operazioni indipendenti. Questo consente l’elaborazione parallela di tutti gli individui, portando alla costruzione di un algoritmo MOEA/D tensorizzato, denominato TensorMOEA/D. In questo algoritmo, la selezione ambientale e divisa in due fasi principali: confronto e aggiornamento della popolazione, e selezione delle soluzioni elite. Queste due fasi sono principalmente tensorizzate attraverso due applicazioni dell’operazione vmap. Il processo dettagliato e illustrato nella Fig. 3.
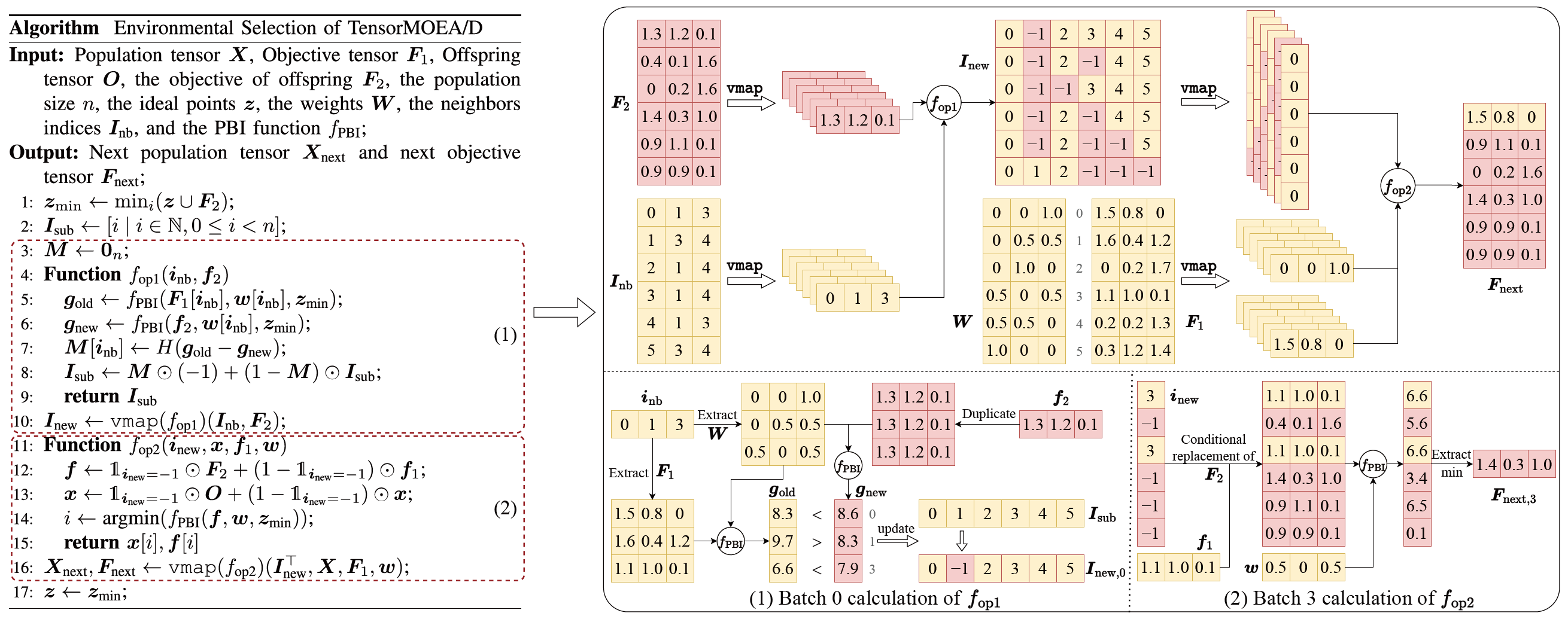
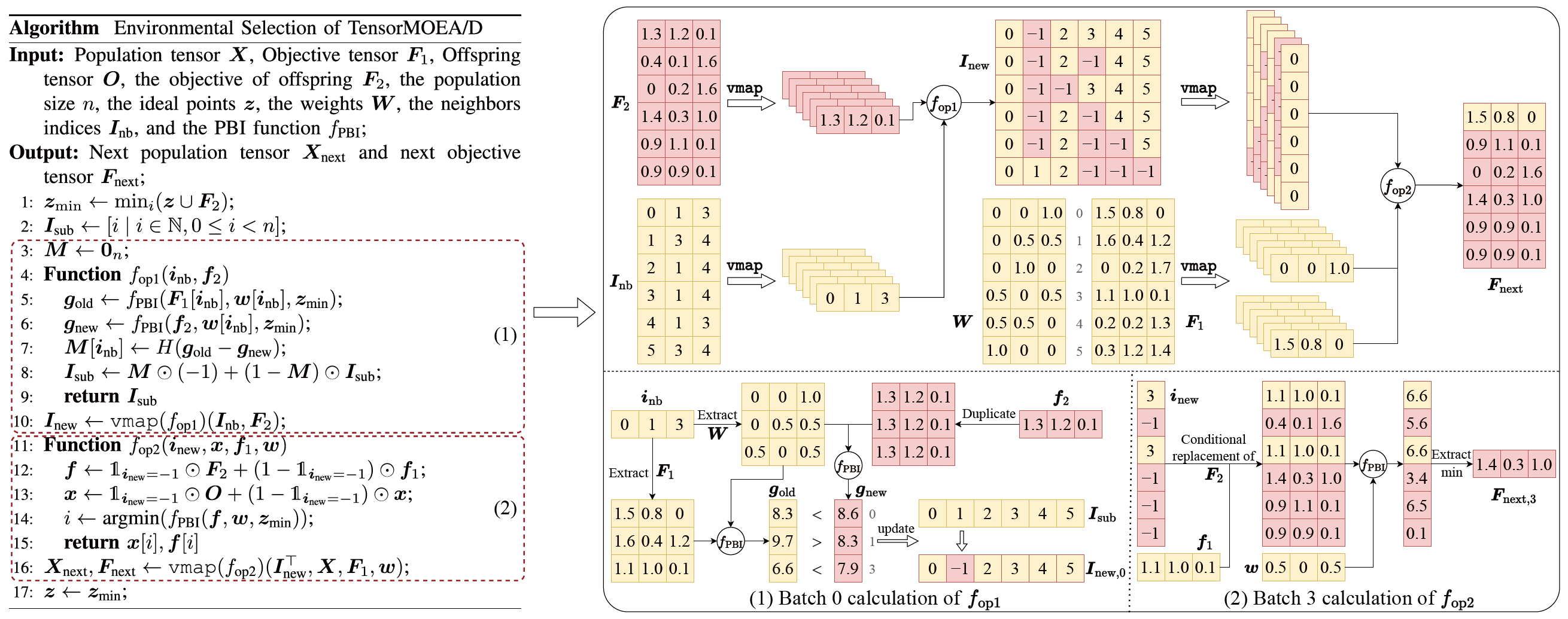
Fig.3: Panoramica della selezione ambientale nell’algoritmo TensorMOEA/D. Sinistra: Pseudocodice dell’algoritmo. Destra: Flusso dati tensoriale del modulo (1) e del modulo (2). La parte superiore della Fig. destra mostra il flusso dati tensoriale complessivo per i moduli (1) e (2), mentre la parte inferiore presenta il flusso dati tensoriale del calcolo batch, con il modulo (1) a sinistra e il modulo (2) a destra.
Per ottenere una comprensione piu completa del valore della tensorizzazione negli algoritmi EMO, si puo riassumere da tre prospettive. In primo luogo, la tensorizzazione consente una trasformazione diretta dalle formulazioni matematiche al codice efficiente, riducendo il divario tra progettazione e implementazione degli algoritmi. Ad esempio, la Fig. 4 illustra come la procedura di ordinamento non dominato tensorizzata possa essere tradotta direttamente dallo pseudocodice al codice Python. In secondo luogo, la tensorizzazione semplifica significativamente la struttura del codice unificando le operazioni a livello di popolazione in una singola rappresentazione tensoriale. Questo riduce la dipendenza da cicli e istruzioni condizionali, migliorando cosi la leggibilita e la manutenibilita del codice. In terzo luogo, la tensorizzazione migliora la riproducibilita degli algoritmi. La sua rappresentazione strutturata facilita i test comparativi e la riproduzione coerente dei risultati.

Fig.4: La trasformazione fluida dell’ordinamento non dominato tensorizzato dallo pseudocodice (sinistra) al codice Python (destra).
Dimostrazione delle prestazioni
Per valutare le prestazioni degli algoritmi di ottimizzazione multi-obiettivo accelerati da GPU, il team EvoX ha condotto sistematicamente tre categorie di esperimenti, concentrandosi sull’accelerazione computazionale, sulle prestazioni di ottimizzazione numerica e sull’efficacia nei compiti di controllo robotico multi-obiettivo.
Prestazioni di accelerazione computazionale:
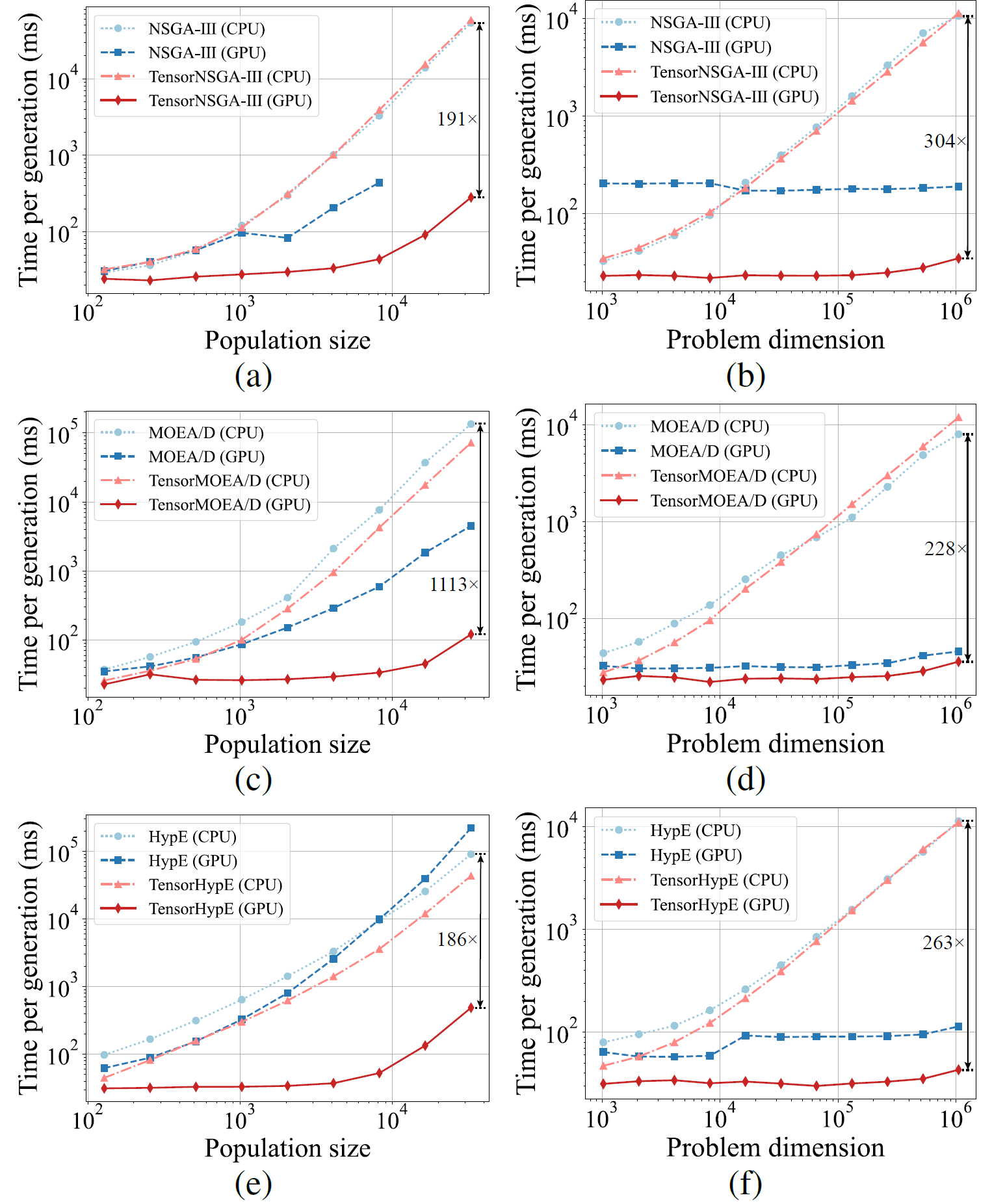
Fig.5: Prestazioni comparative di accelerazione di NSGA-III, MOEA/D e HypE con le loro controparti tensorizzate su piattaforme CPU e GPU con dimensioni della popolazione e dimensioni del problema variabili.
I risultati sperimentali mostrano che TensorNSGA-III, TensorMOEA/D e TensorHypE raggiungono velocita di esecuzione significativamente superiori su GPU rispetto alle loro controparti non tensorizzate basate su CPU. Con l’aumento della dimensione della popolazione e della dimensionalita del problema, lo speedup massimo osservato raggiunge fino a 1113x. Gli algoritmi tensorizzati dimostrano un’eccellente scalabilita e stabilita nella gestione di compiti computazionali su larga scala — il loro tempo di esecuzione aumenta solo marginalmente, mantenendo prestazioni costantemente elevate. Questi risultati evidenziano i sostanziali vantaggi della tensorizzazione per l’accelerazione GPU nell’ottimizzazione multi-obiettivo.
Prestazioni sulla suite di test LSMOP:
Tabella II: Risultati statistici (media e deviazione standard) dell’IGD e del tempo di esecuzione (s) per gli algoritmi EMO non tensorizzati e tensorizzati in LSMOP1—LSMOP9. Tutti gli esperimenti sono su una GPU RTX 4090 e i migliori risultati sono evidenziati.
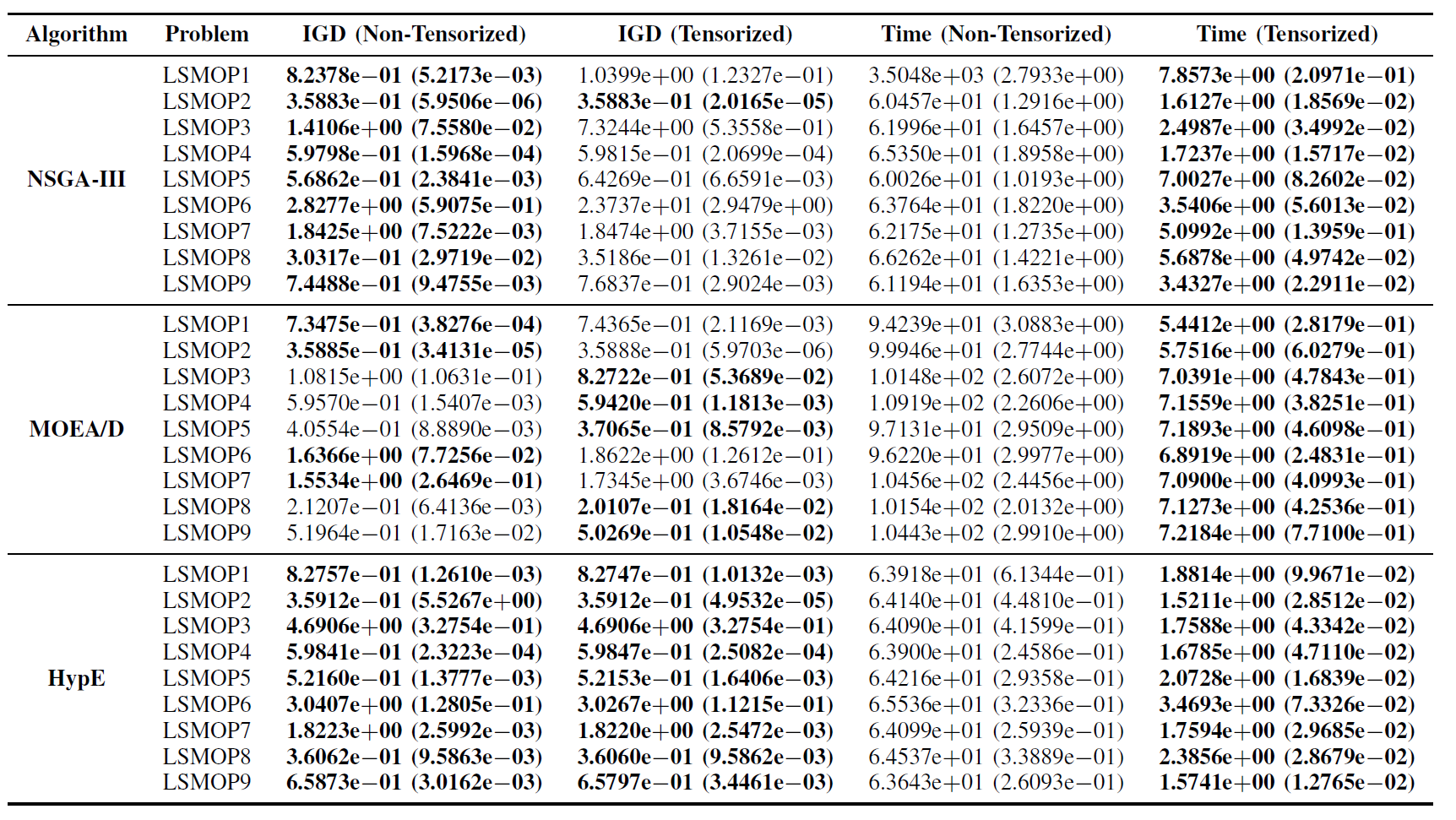
I risultati sperimentali indicano che gli algoritmi EMO accelerati da GPU basati su rappresentazioni tensorizzate migliorano significativamente l’efficienza computazionale mantenendo, e in alcuni casi superando, la precisione di ottimizzazione delle loro controparti originali.
Compiti di controllo robotico multi-obiettivo:
Per valutare in modo completo le prestazioni pratiche degli algoritmi EMO accelerati da GPU, il team ha sviluppato una suite di benchmark denominata MoRobtrol per il controllo robotico multi-obiettivo. I compiti inclusi in questa suite sono elencati nella Tabella III.
Tabella III: Panoramica dei problemi di controllo robotico multi-obiettivo nella suite di benchmark MoRobtrol proposta
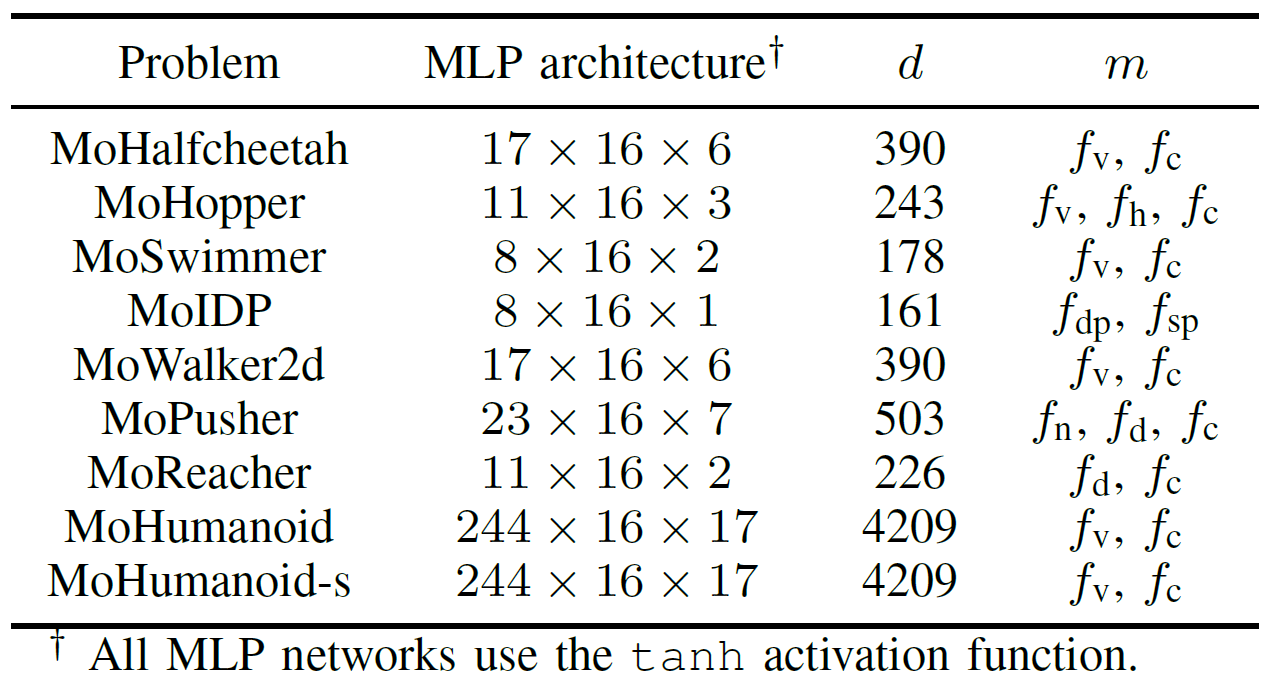
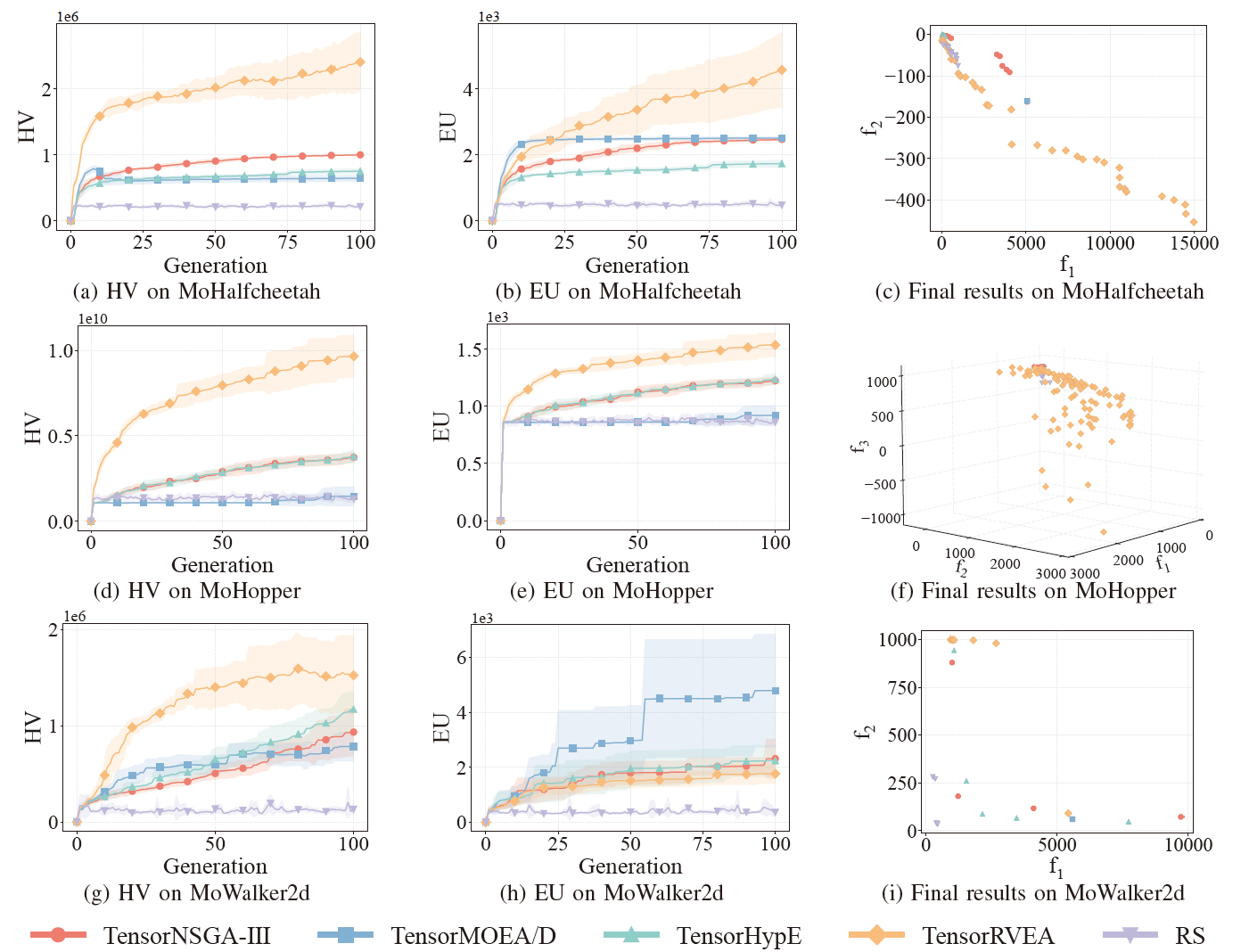
Fig.6: Prestazioni comparative (HV, EU e visualizzazione dei risultati finali) di TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e ricerca casuale (RS) su diversi problemi: MoHalfcheetah (390D), MoHopper (243D) e MoWalker2d (390D). Nota: Valori piu alti per tutte le metriche indicano prestazioni migliori.
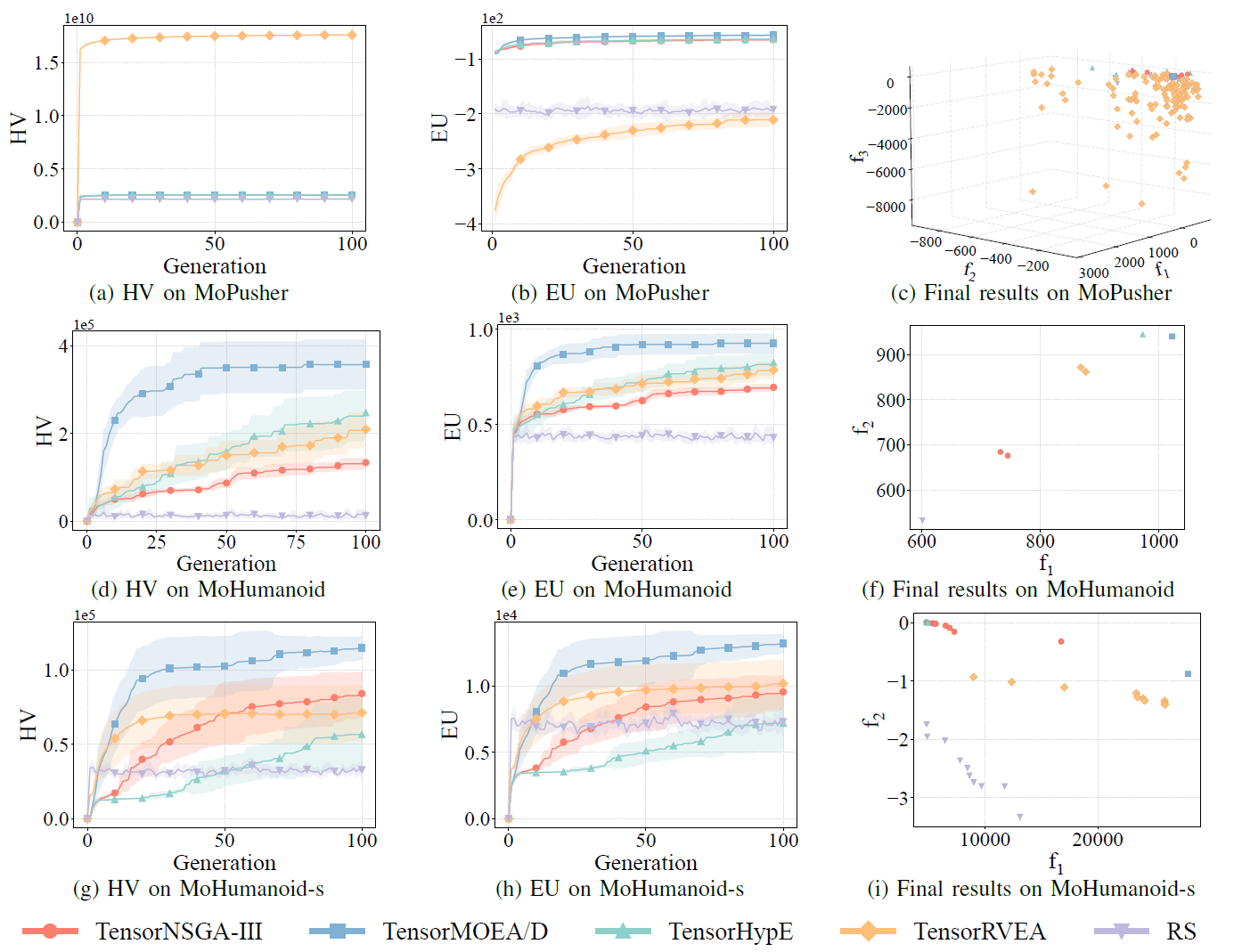
Fig.7: Prestazioni comparative (HV, EU e visualizzazione dei risultati finali) di TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e ricerca casuale (RS) su diversi problemi: MoPusher (503D), MoHumanoid (4209D) e MoHumanoid-s (4209D). Nota: Valori piu alti per tutte le metriche indicano prestazioni migliori.
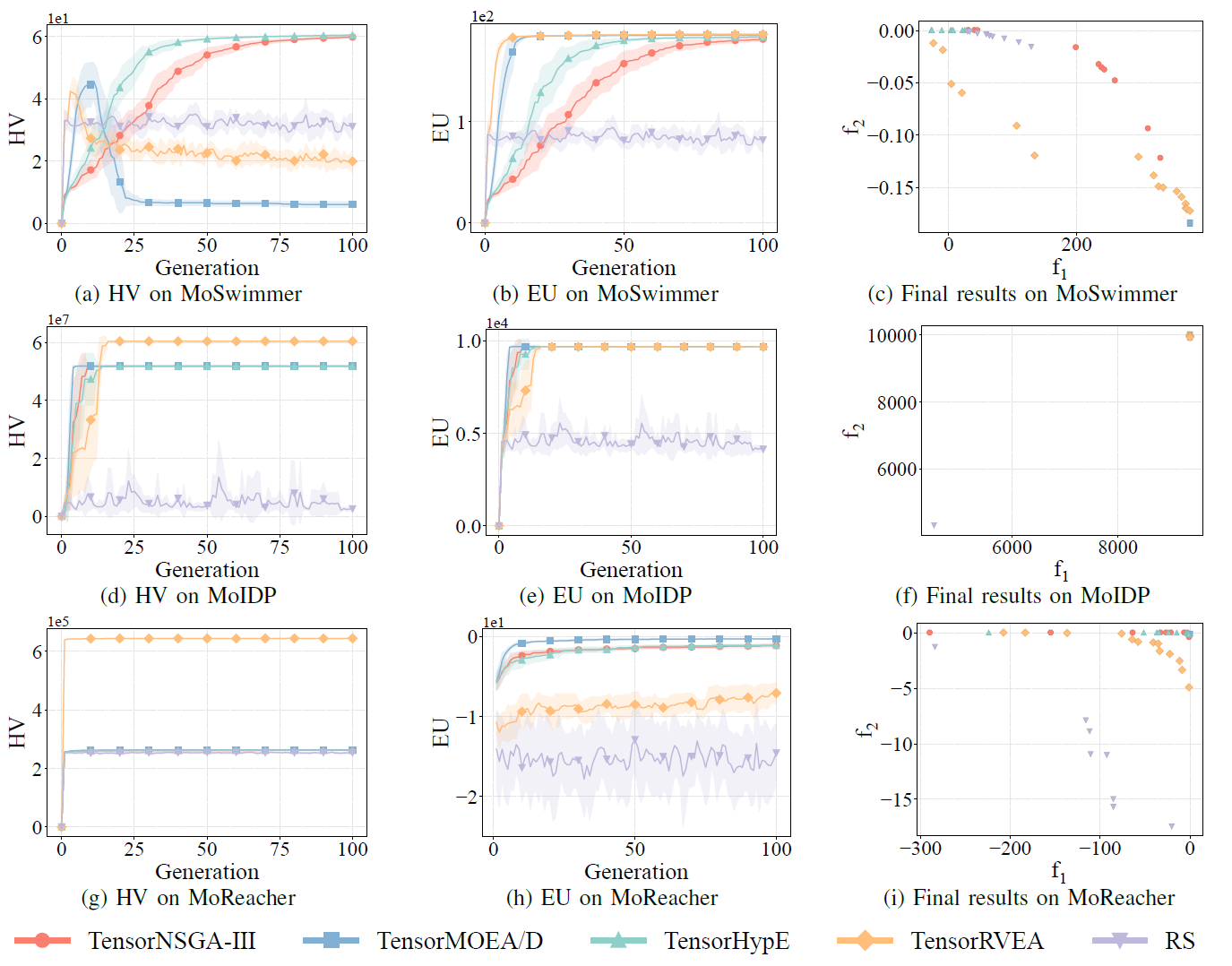
Fig.8: Prestazioni comparative (HV, EU e visualizzazione dei risultati finali) di TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e ricerca casuale (RS) su diversi problemi: MoSwimmer (178D), MoIDP (161D) e MoReacher (226D). Nota: Valori piu alti per tutte le metriche indicano prestazioni migliori.
Gli esperimenti hanno confrontato le prestazioni di TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA e ricerca casuale (RS) all’interno del benchmark MoRobtrol. I risultati mostrano che TensorRVEA ha raggiunto le migliori prestazioni complessive, ottenendo i valori HV piu alti e dimostrando una buona diversita delle soluzioni in molteplici ambienti. TensorMOEA/D ha mostrato una forte adattabilita nei compiti su larga scala, eccellendo in particolare nella coerenza delle preferenze delle soluzioni. TensorNSGA-III e TensorHypE hanno mostrato prestazioni simili e sono stati competitivi in diversi compiti. Nel complesso, gli algoritmi tensorizzati basati sulla decomposizione hanno dimostrato vantaggi superiori nella risoluzione di problemi su larga scala e complessi.
Conclusioni e lavori futuri Questo studio propone una metodologia di rappresentazione tensorizzata per affrontare i limiti degli algoritmi EMO tradizionali basati su CPU in termini di efficienza computazionale e scalabilita. L’approccio e stato applicato a diversi algoritmi rappresentativi, tra cui NSGA-III, MOEA/D e HypE, ottenendo significativi miglioramenti delle prestazioni su GPU mantenendo la qualita delle soluzioni. Per validarne l’applicabilita pratica, il team ha anche sviluppato MoRobtrol, una suite di benchmark per il controllo robotico multi-obiettivo che riformula i compiti di controllo robotico in ambienti di simulazione fisica come problemi di ottimizzazione multi-obiettivo. I risultati dimostrano il potenziale degli algoritmi tensorizzati in scenari computazionalmente intensivi come l’intelligenza incarnata. Sebbene il metodo di tensorizzazione abbia migliorato sostanzialmente l’efficienza algoritmica, c’e ancora spazio per ulteriori miglioramenti. Le direzioni future includono il miglioramento degli operatori fondamentali come l’ordinamento non dominato, la progettazione di nuove operazioni tensorizzate per sistemi multi-GPU e l’integrazione di dati su larga scala e tecniche di deep learning per migliorare ulteriormente le prestazioni sui problemi di ottimizzazione su larga scala.
Codice open source / Risorse della comunita
Paper:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
Progetto upstream (EvoX):
https://github.com/EMI-Group/evox
Gruppo QQ: 297969717

EvoMO e costruito sul framework EvoX. Se sei interessato a saperne di piu su EvoX, consulta l’articolo ufficiale su EvoX 1.0 pubblicato sul nostro account pubblico WeChat per ulteriori dettagli.


