La Differential Evolution (DE), uno de los algoritmos fundamentales de la computación evolutiva, ha sido ampliamente utilizada en problemas de optimización de caja negra gracias a su simplicidad y alta eficiencia. No obstante, su rendimiento depende en gran medida de la selección de hiperparámetros y estrategias, un problema persistente para los investigadores. Para abordar este desafío, el equipo de EvoX publicó recientemente un estudio en IEEE Transactions on Evolutionary Computation (IEEE TEVC) titulado “MetaDE: Evolving Differential Evolution by Differential Evolution”. Como método meta-evolutivo que aprovecha DE para evolucionar sus propios hiperparámetros y estrategias, MetaDE permite el ajuste dinámico de parámetros y estrategias al tiempo que incorpora computación paralela acelerada por GPU. Este diseño mejora sustancialmente la eficiencia computacional junto con el rendimiento de optimización. Los resultados experimentales demuestran que MetaDE ofrece un rendimiento sobresaliente tanto en la suite de benchmarks CEC2022 como en tareas de control robótico. El código fuente de MetaDE está disponible como código abierto en GitHub en https://github.com/EMI-Group/metade.
Contexto
En el campo de la computación evolutiva, el rendimiento de los algoritmos está a menudo significativamente influenciado por la elección de hiperparámetros. Determinar la configuración de parámetros más adecuada para un problema específico ha sido un desafío de investigación de larga data. La Differential Evolution (DE), como algoritmo evolutivo clásico, es ampliamente apreciada por su simplicidad y su robusta capacidad de búsqueda global; sin embargo, su rendimiento es muy sensible a la selección de hiperparámetros. Los métodos convencionales suelen basarse en el ajuste basado en la experiencia o en mecanismos adaptativos para mejorar el rendimiento. No obstante, ante escenarios de problemas diversos, estos enfoques frecuentemente tienen dificultades para equilibrar eficiencia y amplia aplicabilidad.
El concepto de “meta-evolución” se introdujo ya en el siglo pasado, con el objetivo de utilizar los propios algoritmos evolutivos para optimizar las configuraciones de hiperparámetros de estos algoritmos. Aunque la meta-evolución existe desde hace muchos años, su aplicación práctica se ha visto limitada por las elevadas exigencias computacionales. Los avances recientes en computación GPU han aliviado estas restricciones, proporcionando un sólido soporte de hardware para los algoritmos evolutivos. En particular, la introducción del framework EvoX con aceleración GPU distribuida ha facilitado enormemente el desarrollo de algoritmos evolutivos basados en GPU. En este contexto, nuestro equipo de investigación propuso un novedoso enfoque de meta-evolución que aprovecha DE para evolucionar sus propios hiperparámetros y estrategias, ofreciendo así una nueva vía para resolver el problema de larga data del ajuste de parámetros en algoritmos evolutivos.
¿Qué es la meta-evolución?
La idea central de la meta-evolución puede resumirse como “utilizar un algoritmo evolutivo para evolucionar a sí mismo” (Evolving an Evolutionary Algorithm by an Evolutionary Algorithm). Este concepto trasciende los métodos tradicionales de computación evolutiva al no solo emplear algoritmos evolutivos para buscar soluciones óptimas a un problema, sino también adaptar los hiperparámetros y estrategias de los algoritmos a través de sus propios procesos evolutivos.
En otras palabras, la meta-evolución introduce un paradigma de “autoevolución”, que permite a los algoritmos optimizarse a sí mismos mientras exploran el espacio de búsqueda en busca de soluciones al problema. Al refinarse continuamente durante el proceso evolutivo, los algoritmos se vuelven más adaptativos y pueden mantener una alta eficiencia en diversos escenarios de problemas.
Tomando MetaDE como ejemplo, su diseño se fundamenta en esta filosofía. En una estructura de dos capas, la capa inferior (el “ejecutor”) resuelve el problema de optimización dado utilizando una DE parametrizada. La capa superior (el “evolucionador”) emplea simultáneamente DE para optimizar las configuraciones de hiperparámetros del ejecutor. Este framework permite que DE no solo sirva como solucionador, sino que también “explore” cómo ajustar mejor sus propios parámetros y estrategias para resolver diferentes problemas de manera más eficaz. Este proceso es similar a un sistema que se comprende y se refina incrementalmente a sí mismo: una transformación de “resolver pasivamente un problema” a “autoevolucionar activamente”. En consecuencia, puede adaptarse mejor a tareas diversas. Si consideramos DE como un sistema complejo, MetaDE permite efectivamente una forma “recursiva” de autocomprensión y automejora dentro de este sistema. El término “recursión” en informática describe típicamente una función o procedimiento que se llama a sí mismo. Dentro de MetaDE, este concepto adquiere un nuevo significado: es un mecanismo de optimización internamente recursivo que emplea DE para evolucionar los hiperparámetros de DE. Este esquema autorreferencial no solo encarna una potente adaptabilidad, sino que también proporciona una perspectiva novedosa sobre el teorema de “no hay almuerzo gratis”. Dado que no existe un conjunto único de parámetros universalmente óptimo para todos los problemas, permitir que el algoritmo evolucione por sí mismo de forma autónoma es clave para encontrar las mejores configuraciones de parámetros para una tarea dada.
A través de este enfoque meta-evolutivo recursivo, MetaDE logra varios beneficios:
1. Ajuste automatizado de parámetros
Se elimina el laborioso proceso de ajuste manual. El propio algoritmo aprende a ajustar sus hiperparámetros, reduciendo la intervención humana y mejorando la eficiencia.2. Adaptabilidad mejorada
MetaDE responde dinámicamente a las características y condiciones cambiantes del problema, modificando estrategias en tiempo real para mejorar el rendimiento. Esto aumenta significativamente la flexibilidad del algoritmo.3. Búsqueda eficiente Al aprovechar el paralelismo inherente, MetaDE acelera enormemente las búsquedas en problemas de optimización a gran escala. Ofrece soluciones viables a problemas complejos de alta dimensionalidad en plazos razonables.
Implementación algorítmica
MetaDE emplea técnicas basadas en tensores y aceleración GPU para permitir una computación paralela eficiente. Al procesar simultáneamente muchos individuos de una población, la eficiencia computacional global mejora notablemente, lo que resulta particularmente ventajoso en la optimización de caja negra mono-objetivo y en problemas de optimización a gran escala. Mediante la tensorización de parámetros y estructuras de datos clave (por ejemplo, población, aptitud, parámetros de estrategia), MetaDE no solo logra una mayor eficiencia computacional, sino que también mejora su capacidad para abordar desafíos de optimización complejos. En comparación con la DE clásica y otros algoritmos evolutivos (EAs), MetaDE muestra un rendimiento superior en la resolución de problemas a gran escala. Gracias al enfoque basado en tensores, MetaDE aprovecha los recursos computacionales de manera más eficaz, obteniendo soluciones más rápidas y resultados de optimización más precisos que los métodos tradicionales.
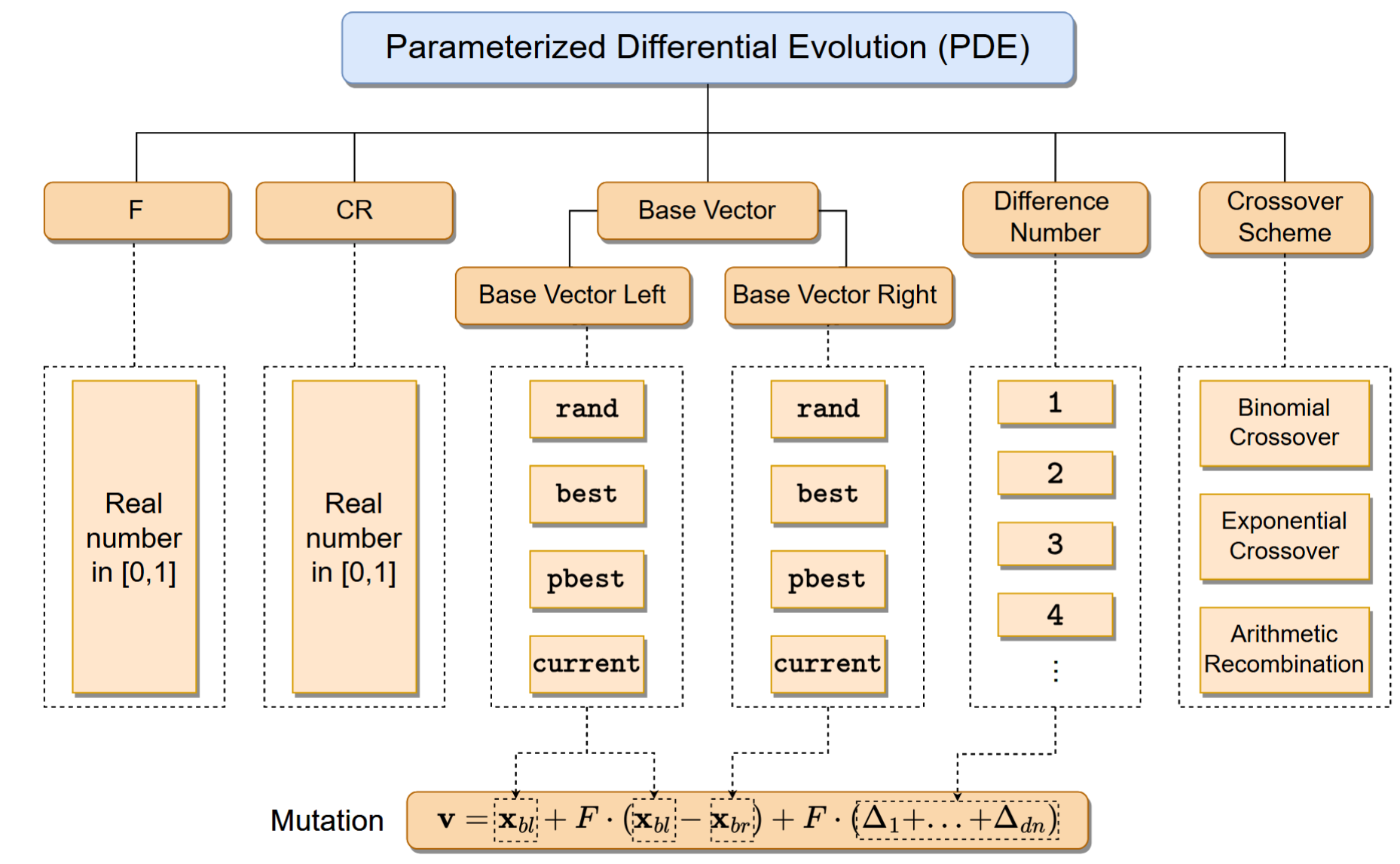
Arquitectura de PDE
El equipo de investigación propuso primero un framework de algoritmo DE parametrizado (PDE) que soporta completamente la modificación de parámetros y estrategias. En este framework, F y CR son parámetros continuos, mientras que los demás parámetros son discretos. Los recuadros discontinuos indican el rango de valores de parámetros permitidos. La función de mutación se deriva de los vectores base izquierdo y derecho, junto con el parámetro que controla el número de vectores de diferencia.
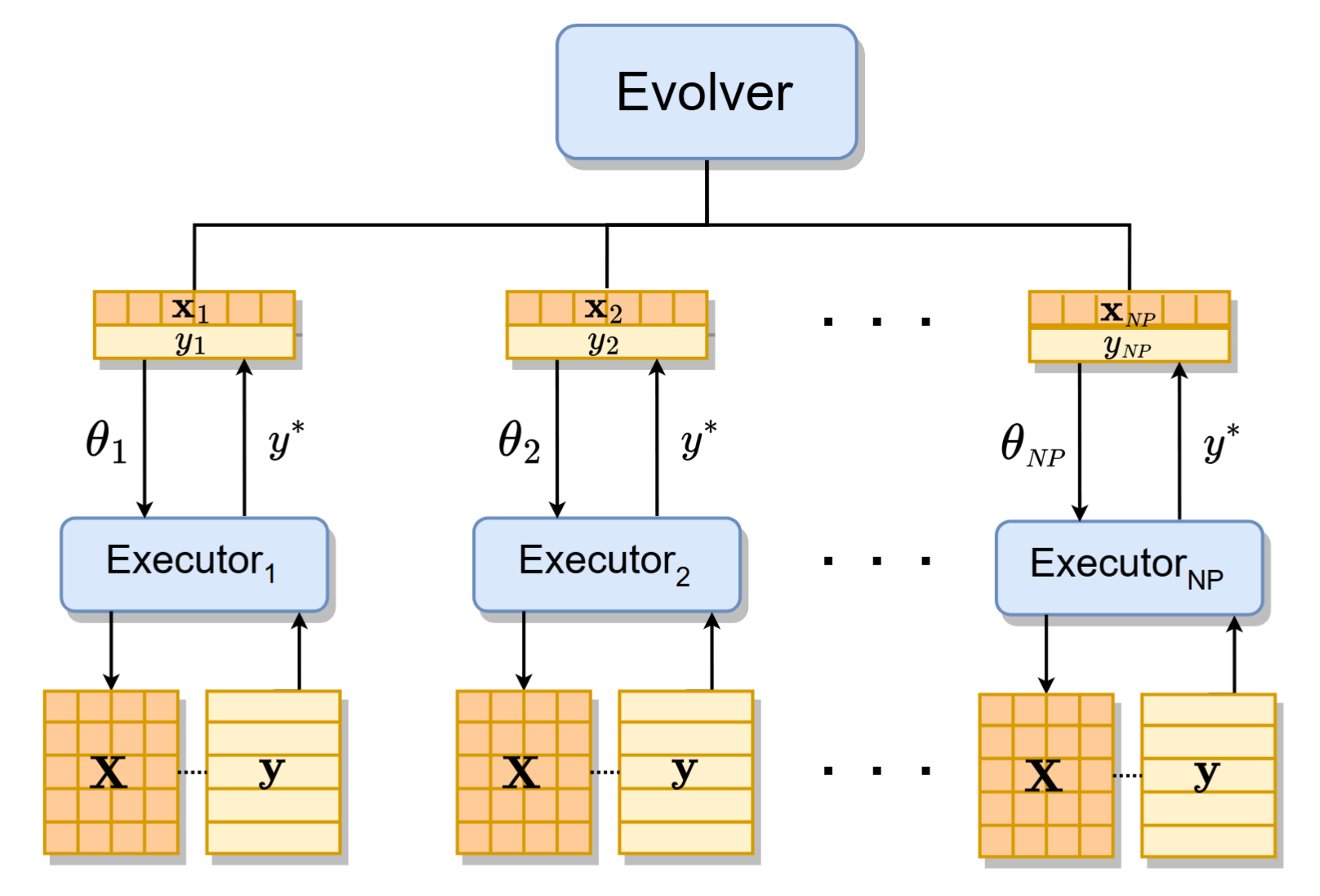
Arquitectura de MetaDE
MetaDE adopta una estructura de dos capas, compuesta por un evolucionador (capa superior) y múltiples ejecutores (capa inferior). El evolucionador es una DE (o potencialmente otro algoritmo evolutivo), responsable de optimizar los parámetros de PDE. Cada individuo
x_i en la población del evolucionador corresponde a una configuración de parámetros única θ_i. Estas configuraciones se pasan a PDE para instanciar diferentes variantes de DE, cada una gestionada por un ejecutor que se ejecuta de forma independiente en la tarea de optimización dada. Cada ejecutor devuelve su mejor valor de aptitud y^* al evolucionador, que asigna ese valor de aptitud y_i al individuo correspondiente x_i.
Rendimiento experimental
Para evaluar de forma exhaustiva la eficacia de MetaDE, el equipo de investigación realizó experimentos sistemáticos que abarcan múltiples pruebas de referencia y escenarios del mundo real. Cada experimento utilizó un evolucionador (DE con estrategia rand/1/bin) y ejecutores (PDE con un tamaño de población de 100). Los componentes experimentales clave incluyen:
Benchmark CEC2022 Comparación de MetaDE con diversas variantes de DE en tareas de optimización mono-objetivo.
Comparación con los cuatro mejores algoritmos de CEC2022 Evaluación de MetaDE frente a los cuatro algoritmos con mejor rendimiento de la competición CEC2022 bajo presupuestos idénticos de evaluaciones de función (FEs).
Evaluaciones de función (FEs) bajo tiempo de ejecución fijo Análisis de la eficiencia computacional de MetaDE bajo aceleración GPU.
Tareas de control robótico Aplicación de MetaDE a tareas de control robótico en un entorno de la plataforma Brax para validar su utilidad práctica.
Benchmark CEC2022: comparación con variantes principales de DE
El equipo comparó MetaDE con varias variantes representativas de DE en la suite de benchmarks CEC2022, incluyendo:
- Standard DE (rand/1/bin)
- SaDE y JaDE (algoritmos DE adaptativos)
- CoDE (DE con integración de estrategias)
- SHADE y LSHADE-RSP (DE adaptativa basada en historial de éxitos)
- EDEV (variantes DE integradas)
Todos los algoritmos se implementaron en la plataforma EvoX, utilizando aceleración GPU con un tamaño de población de 100 para garantizar la equidad. Los experimentos se realizaron en diferentes dimensionalidades (10D y 20D) bajo la misma restricción de tiempo computacional (60 segundos).
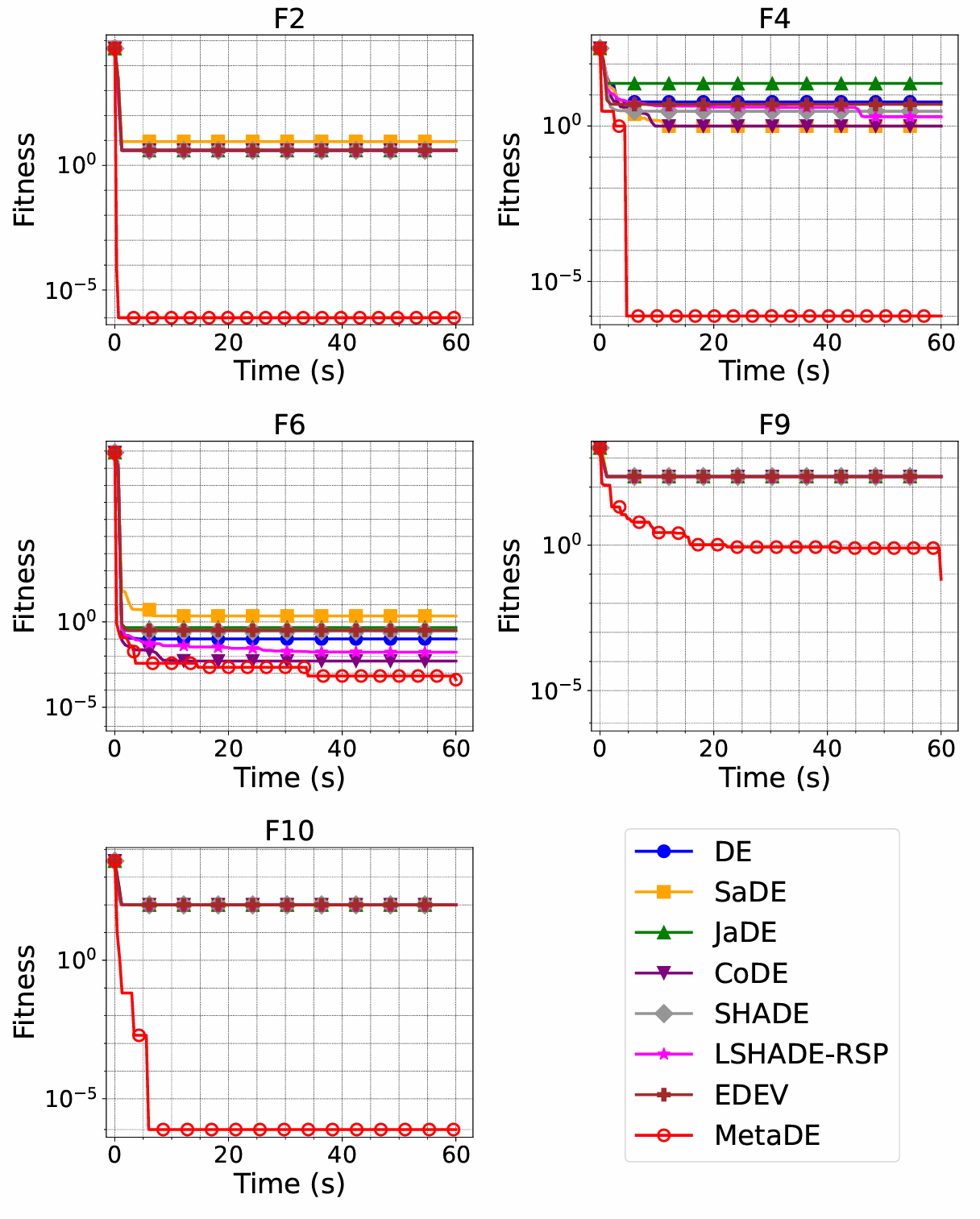
Resultados de optimización CEC2022 en 10D
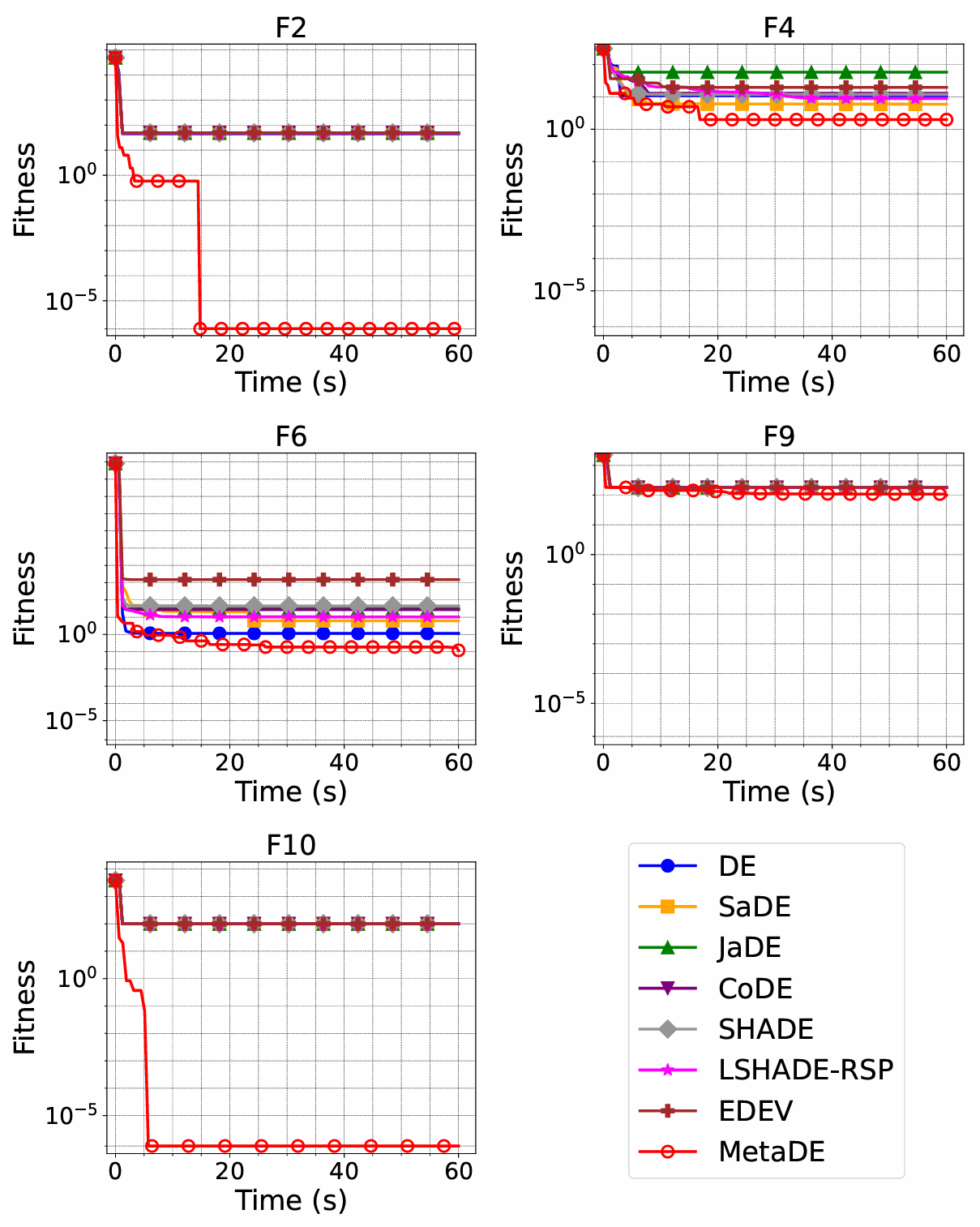
Resultados de optimización CEC2022 en 20D
MetaDE generalmente logra una convergencia más rápida y estable en la mayoría de las funciones de prueba. Su DE parametrizada (PDE) combinada con la optimización de la capa superior permite una adaptación dinámica a diferentes espacios de problemas, mejorando la robustez general y el rendimiento de búsqueda.
Comparación con los cuatro mejores algoritmos de CEC2022 (bajo FEs idénticas)
Para evaluar aún más la capacidad de optimización de MetaDE, lo comparamos con los cuatro mejores algoritmos de la competición CEC2022 dentro del mismo presupuesto de evaluaciones de función:
- EA4eig: Un método híbrido que integra múltiples EAs
- NL-SHADE-LBC: Una DE adaptativa mejorada
- NL-SHADE-RSP-MID: Un SHADE mejorado con estimación de punto medio
- S-LSHADE-DP: Una variante de DE que mantiene la diversidad poblacional mediante perturbación dinámica
Cada uno de estos algoritmos se ejecutó con sus configuraciones de parámetros oficiales y código fuente bajo las mismas restricciones de FE. Se realizaron comparaciones estadísticas (prueba de suma de rangos de Wilcoxon, nivel de significación 0,05)
entre MetaDE y cada línea base en la suite de pruebas CEC2022. La última fila de la tabla muestra el rendimiento de cada algoritmo en comparación con MetaDE en las diferentes funciones de prueba: + (significativamente mejor), ≈ (sin diferencia significativa) y − (significativamente peor).
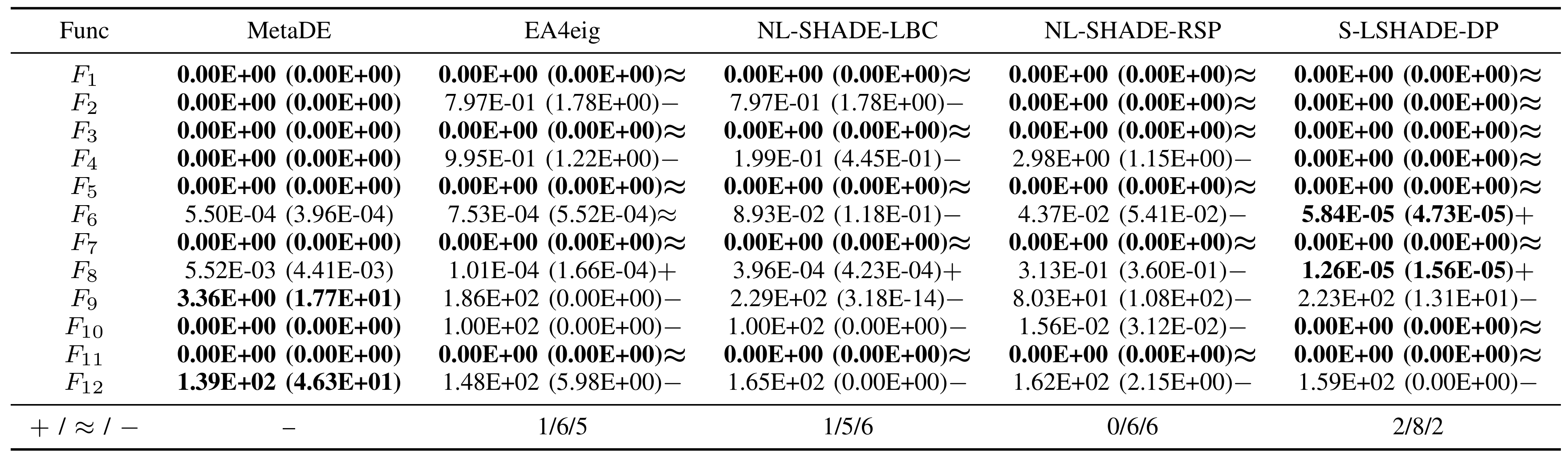
Comparación de algoritmos de la competición CEC2022 en 10D (mismas FEs)
Comparación de algoritmos de la competición CEC2022 en 20D (mismas FEs)
MetaDE demuestra consistentemente un rendimiento sólido, especialmente en problemas complejos que requieren una convergencia robusta. Gracias a su mecanismo autoadaptativo, MetaDE ajusta eficazmente su estrategia para diferentes paisajes de búsqueda, mejorando así la eficiencia de búsqueda y la capacidad de optimización global. Estos resultados indican que MetaDE no solo supera a las variantes principales de DE, sino que también exhibe una fuerte competitividad frente a los algoritmos de primer nivel de la competición.
Eficiencia computacional: FEs en un tiempo fijo (60 segundos)
El equipo de investigación registró además el número de evaluaciones de función (FEs) completadas por los diferentes algoritmos dentro del mismo tiempo de ejecución fijo (60 segundos).
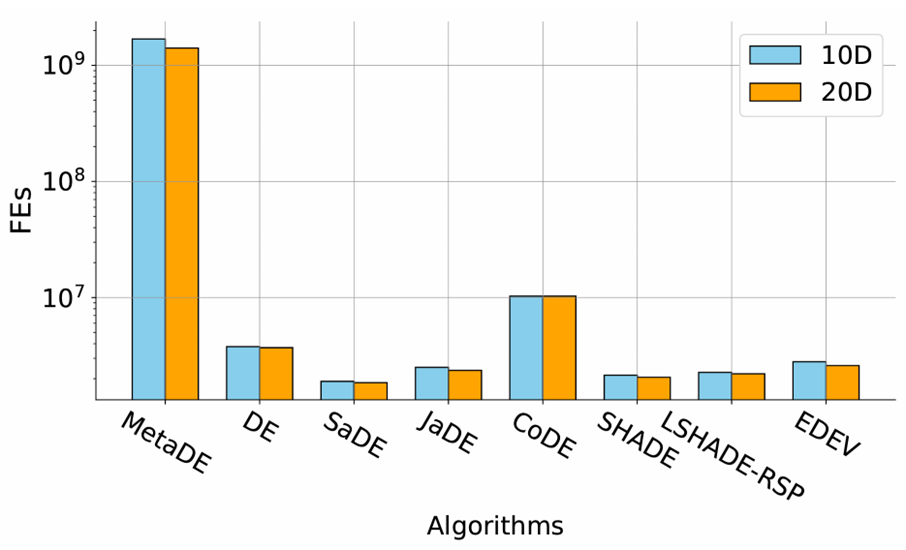
FEs alcanzadas por cada algoritmo en 60 segundosBajo el mismo framework EvoX con computación paralela acelerada por GPU, MetaDE alcanzó en promedio FEs del nivel de 10****⁹, mientras que las variantes tradicionales de DE solo alcanzaron alrededor de 10^6 FEs. Esta ventaja surge del enfoque parametrizado de MetaDE, que realiza evaluaciones paralelas a gran escala de individuos, permitiendo una utilización más eficiente de los recursos de hardware. En consecuencia, el algoritmo explora más soluciones dentro de la misma ventana temporal, mejorando tanto la calidad de las soluciones como la estabilidad.
Aprendizaje por refuerzo evolutivo: tareas de control robótico
En el aprendizaje por refuerzo (RL), la eficiencia y la estabilidad de la optimización de políticas son cruciales. Los métodos basados en gradientes como PPO y SAC pueden sufrir de desvanecimiento o explosión de gradientes en entornos de alta dimensionalidad. En contraste, el aprendizaje por refuerzo evolutivo (EvoRL) evita estos problemas utilizando búsquedas libres de gradientes para optimizar directamente los parámetros de las políticas.
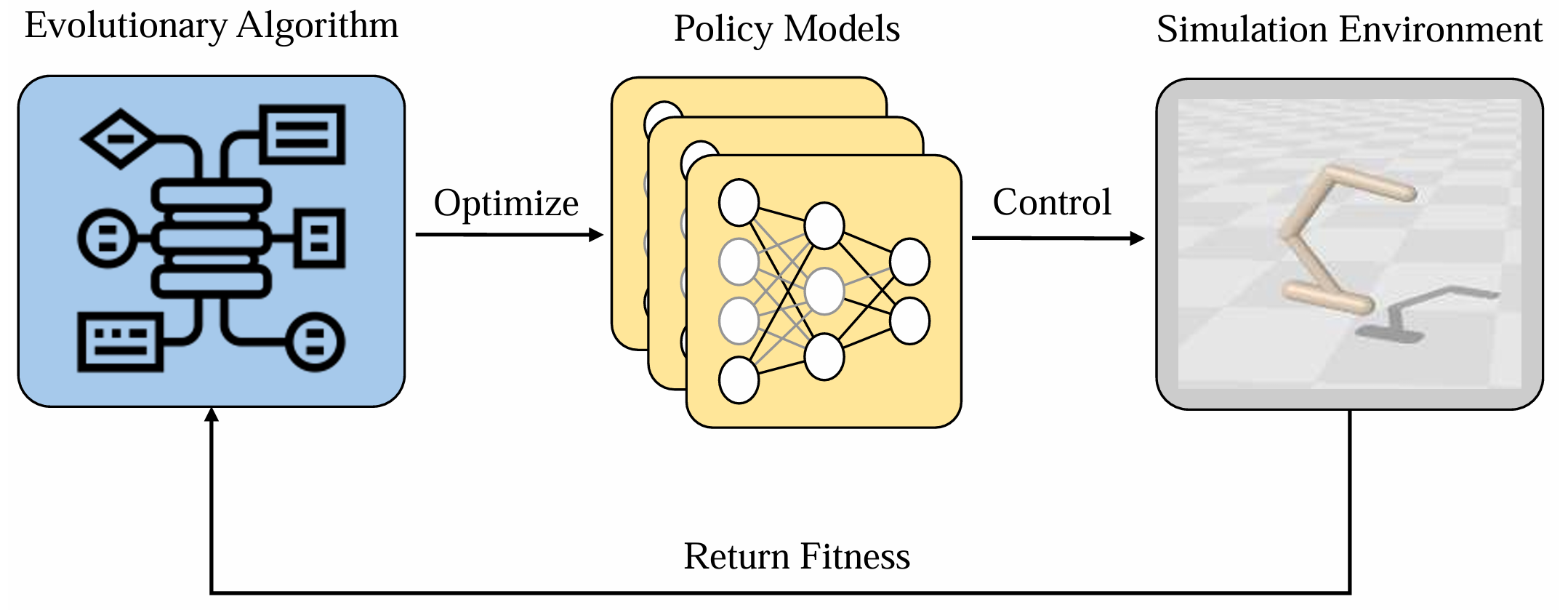
Proceso de aprendizaje por refuerzo evolutivo
Dentro del framework EvoRL, MetaDE:
- Optimiza automáticamente los parámetros de redes neuronales, aumentando la adaptabilidad de los modelos de políticas.
- Ajusta dinámicamente los hiperparámetros, mejorando la estabilidad del entrenamiento.
- Aprovecha la aceleración GPU para acelerar la optimización de políticas.
Para evaluar el rendimiento de MetaDE en tareas de optimización complejas, lo aplicamos a problemas de control robótico utilizando optimización acelerada por GPU en la plataforma de simulación Brax. El estudio incluyó tres tareas —Swimmer, Hopper y Reacher— cada una modelada por una red neuronal totalmente conectada de tres capas (MLP) con el objetivo de maximizar la recompensa. Cabe destacar que cada MLP contiene aproximadamente 1.500 parámetros, creando un desafío de optimización de 1.500 dimensiones para los algoritmos evolutivos (EAs). Esto impone requisitos estrictos tanto en capacidad de búsqueda como en eficiencia computacional.
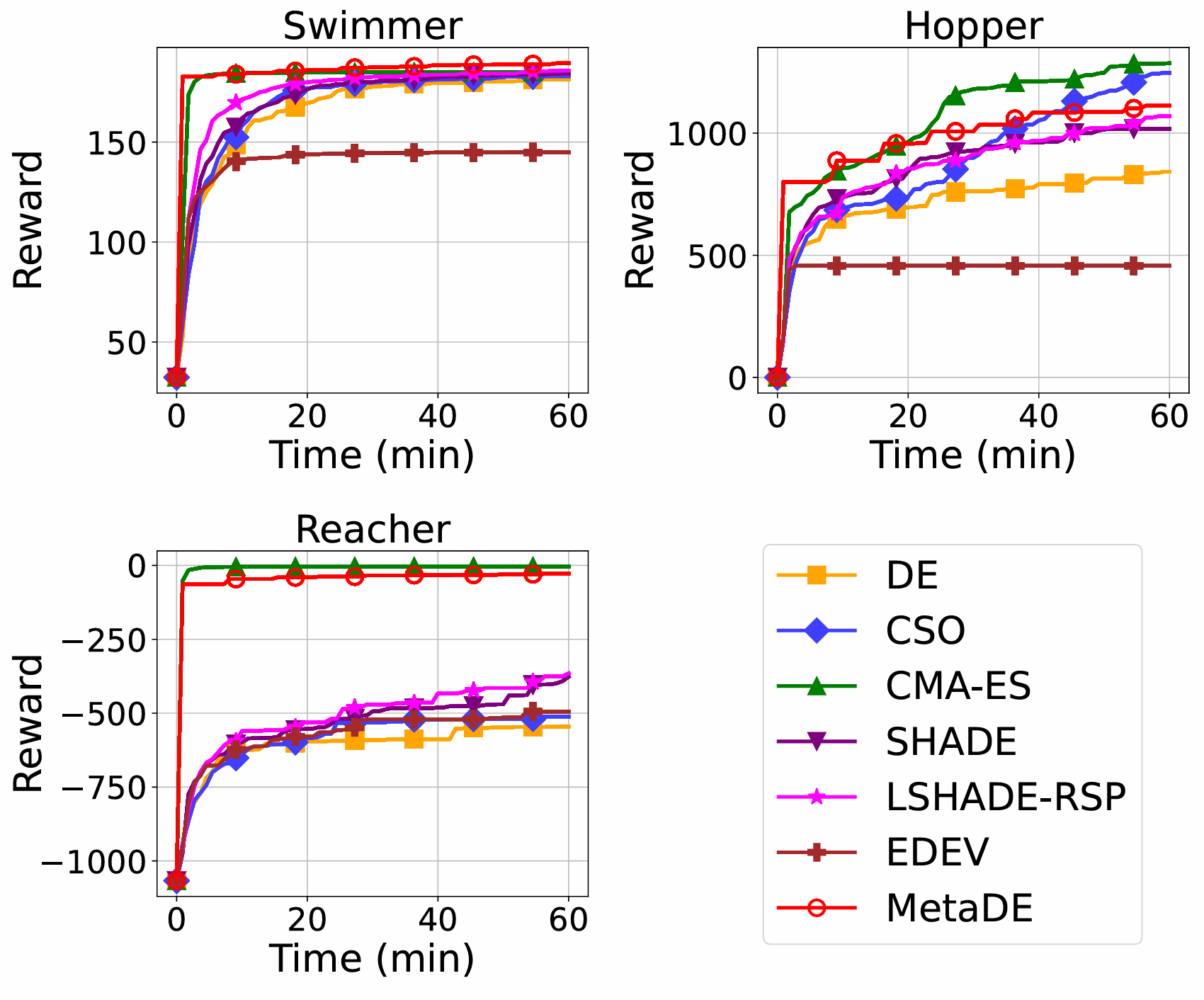
Curvas de convergencia para tres entornos Brax
Como se muestra en la figura, MetaDE demuestra un rendimiento sólido en tareas de control robótico basadas en Brax, logrando los mejores resultados en la tarea Swimmer y resultados casi óptimos en Hopper y Reacher. Su principal ventaja reside en la alta calidad de la población inicial, que permite una convergencia rápida en las primeras etapas y produce soluciones de alta calidad. Estos hallazgos sugieren que MetaDE puede optimizar eficientemente las políticas de redes neuronales, lo que lo hace idóneo para tareas de control robótico con simulaciones físicas complejas y ofrece un amplio potencial para aplicaciones prácticas.
Conclusión y direcciones futuras
MetaDE es un enfoque innovador de meta-evolución que no solo destaca en la resolución de tareas de optimización, sino que también ajusta y refina autónomamente sus propias estrategias. Aprovechando las fortalezas de la Differential Evolution, MetaDE exhibe un gran potencial en la configuración adaptativa de parámetros y la evolución de estrategias. Los resultados experimentales muestran una robustez superior en una variedad de pruebas de referencia, y su aplicabilidad en el mundo real queda demostrada por el éxito en tareas de control robótico mediante aprendizaje por refuerzo evolutivo. Un desafío central implica mantener un equilibrio óptimo entre generalización y especialización, asegurando que el algoritmo pueda adaptarse a tareas diversas y al mismo tiempo optimizar eficazmente para problemas específicos. Esta investigación ofrece nuevas perspectivas para los algoritmos evolutivos autoadaptativos y puede impulsar nuevos avances en meta-evolución para sistemas complejos.
Código abierto y comunidad
Paper: https://arxiv.org/abs/2502.10470
GitHub: https://github.com/EMI-Group/metade
Proyecto principal (EvoX): https://github.com/EMI-Group/evox
Grupo QQ: 297969717
Grupo QQ | Evolving Machine Intelligence
MetaDE está construido sobre el framework EvoX. Si está interesado en EvoX, consulte el artículo sobre EvoX 1.0 para más detalles.
(https://mp.weixin.qq.com/s/uT6qSqiWiqevPRRTAVIusQ)
