Verbindung von evolutionaerer Mehrzieloptimierung
und GPU-Beschleunigung durch Tensorisierung
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
Mit dem stetig wachsenden Bedarf an komplexen Optimierungsloesungen in Bereichen wie Ingenieurdesign und Energiemanagement haben evolutionaere Mehrzieloptimierungs-Algorithmen (EMO) aufgrund ihrer robusten Faehigkeiten bei der Loesung mehrkriterieller Probleme breite Aufmerksamkeit erlangt. Da Optimierungsaufgaben jedoch an Umfang und Komplexitaet zunehmen, stossen traditionelle CPU-basierte EMO-Algorithmen auf erhebliche Leistungsengpaesse.
Um diese Einschraenkung zu ueberwinden, schlug das EvoX-Team vor, EMO-Algorithmen mittels der Tensorisierungsmethodik auf GPUs zu parallelisieren. Mit dieser Methode haben sie erfolgreich mehrere GPU-beschleunigte EMO-Algorithmen entworfen und implementiert. Darueber hinaus entwickelte das Team “MoRobtrol”, eine Benchmark-Suite fuer mehrkriterielle Robotersteuerung, die auf der Brax-Physik-Engine basiert und darauf abzielt, die Leistung GPU-beschleunigter EMO-Algorithmen systematisch zu bewerten.
Basierend auf diesen Forschungsfortschritten hat das EvoX-Team EvoMO veroeffentlicht, eine leistungsstarke GPU-beschleunigte EMO-Algorithmen-Bibliothek. Der entsprechende Quellcode ist oeffentlich auf GitHub verfuegbar: https://github.com/EMl-Group/evomo
Tensorisierungsmethodik
Im Bereich der rechnergestuetzten Optimierung bezeichnet ein Tensor eine mehrdimensionale Array-Datenstruktur, die Skalare, Vektoren, Matrizen und hoeherwertige Daten darstellen kann. Tensorisierung ist der Prozess der Umwandlung von Datenstrukturen und Operationen innerhalb eines Algorithmus in Tensorform, wodurch der Algorithmus die parallelen Rechenfaehigkeiten von GPUs voll ausschoepfen kann.
In EMO-Algorithmen koennen alle wichtigen Datenstrukturen in tensorisierter Form ausgedrueckt werden. Die Individuen einer Population koennen durch einen Loesungstensor X dargestellt werden, wobei jeder Zeilenvektor einem Individuum entspricht. Die Zielfunktionswerte bilden einen Zieltensor F. Zusaetzlich koennen Hilfsdatenstrukturen wie Referenzvektoren und Gewichtsvektoren als Tensoren R bzw. W ausgedrueckt werden. Diese einheitliche Tensordarstellung ermoeglicht Operationen auf Populationsebene auf der Darstellungsebene und legt eine solide Grundlage fuer grossskalige parallele Berechnung.
Die Tensorisierung von EMO-Algorithmus-Operationen ist entscheidend fuer die Steigerung der Recheneffizienz und kann in zwei Ebenen unterteilt werden: grundlegende Tensoroperationen und Kontrollfluss-Tensorisierung. Grundlegende Tensoroperationen bilden den Kern der tensorisierten Implementierung von EMO-Algorithmen, wie in Tabelle I detailliert beschrieben.
Tabelle I: Grundlegende Tensoroperationen

Die Kontrollfluss-Tensorisierung ersetzt traditionelle Schleifen- und Bedingungslogik durch parallelisierbare Tensoroperationen. Beispielsweise koennen for/while-Schleifen durch Broadcasting-Mechanismen oder hoeherwertige Funktionen wie vmap in Batch-Operationen umgewandelt werden. Ebenso koennen if-else-Bedingungen durch Maskierungstechniken ersetzt werden, bei denen logische Bedingungen als boolesche Tensoren kodiert werden, was ein flexibles Umschalten zwischen verschiedenen Berechnungspfaden ermoeglicht.
Im Vergleich zu traditionellen EMO-Algorithmus-Implementierungen bietet der Tensorisierungsansatz erhebliche Vorteile. Erstens bietet er groessere Flexibilitaet und verarbeitet mehrdimensionale Daten auf natuerliche Weise, waehrend konventionelle Methoden oft auf zweidimensionale Matrixoperationen beschraenkt sind. Zweitens verbessert die Tensorisierung die Recheneffizienz durch parallele Ausfuehrung erheblich und vermeidet den Overhead, der mit expliziten Schleifen und bedingten Verzweigungen verbunden ist. Schliesslich vereinfacht sie die Codestruktur und fuehrt zu praezisenren und wartbareren Programmen.
Wie in Abb. 1 dargestellt, stuetzt sich beispielsweise die traditionelle Implementierung der Pareto-Dominanzpruefung auf verschachtelte Schleifen fuer elementweise Vergleiche. Im Gegensatz dazu erreicht die tensorisierte Version dieselbe Funktionalitaet durch Broadcasting- und Maskierungsoperationen, die eine parallele Auswertung ermoeglichen. Dies reduziert nicht nur die Code-Komplexitaet, sondern verbessert auch die Laufzeitleistung dramatisch.

Abb.1: Vergleich zwischen konventioneller und tensorbasierter Implementierung der Pareto-Dominanzerkennung.
Aus einer tieferen Perspektive eignet sich die Tensorisierung gut fuer GPU-Beschleunigung, da GPUs eine grosse Anzahl paralleler Kerne besitzen und ihre Single-Instruction-Multiple-Thread (SIMT)-Architektur natuerlich mit Tensorberechnungen harmoniert, insbesondere bei Matrixoperationen. Dedizierte Hardware wie NVIDIAs Tensor Cores steigert den Durchsatz von Tensoroperationen weiter. Im Allgemeinen sind Algorithmen, die hohe Parallelitaet aufweisen, unabhaengige Rechenaufgaben enthalten und minimale bedingte Verzweigungen haben, besser fuer die Tensorisierung geeignet. Bei Algorithmen wie MOEA/D, die sequenzielle Abhaengigkeiten aufweisen, stellt die inhaerent Struktur Herausforderungen fuer die direkte Tensorisierung dar. Durch strukturelle Umgestaltung und Entkopplung kritischer Berechnungen ist es jedoch moeglich, eine effektive parallele Beschleunigung zu erreichen.
Anwendungsbeispiel der Algorithmus-Tensorisierung
Basierend auf der tensorisierten Darstellungsmethodik hat das EvoX-Team tensorisierte Versionen von drei klassischen EMO-Algorithmen entworfen und implementiert: den dominanzbasierten NSGA-III, den zerlegungsbasierten MOEA/D und den indikatorbasierten HypE. Der folgende Abschnitt bietet eine detaillierte Erklaerung am Beispiel von MOEA/D. Tensorisierte Implementierungen von NSGA-III und HypE finden sich in der referenzierten Arbeit.
Wie in Abb. 2 dargestellt, zerlegt der traditionelle MOEA/D ein mehrkriterielles Problem in mehrere Teilprobleme, von denen jedes unabhaengig optimiert wird. Der Algorithmus umfasst vier Kernschritte: Crossover und Mutation, Fitnessbewertung, Idealpunkt-Aktualisierung und Nachbarschafts-Aktualisierung. Diese Schritte werden fuer jedes Individuum innerhalb einer einzelnen Schleife sequenziell ausgefuehrt. Diese sequenzielle Verarbeitung fuehrt bei grossen Populationen zu erheblichem Rechenaufwand, da jedes Individuum alle Schritte der Reihe nach abschliessen muss, was die potenziellen Vorteile der GPU-Beschleunigung einschraenkt. Insbesondere die Nachbarschafts-Aktualisierung beruht auf Interaktionen zwischen Individuen, was die Parallelisierung weiter erschwert.

Abb.2: Pseudocode von MOEA/D
Um das Problem der sequenziellen Abhaengigkeiten im traditionellen MOEA/D zu loesen, fuehrte das Team eine tensorisierte Darstellungsmethode innerhalb der inneren Schleife der Umweltselektion ein. Durch die Entkopplung von Crossover und Mutation, Fitnessbewertung, Idealpunkt-Aktualisierung und Nachbarschafts-Aktualisierung werden diese Komponenten als unabhaengige Operationen behandelt. Dies ermoeglicht die parallele Verarbeitung aller Individuen und fuehrt zur Konstruktion eines tensorisierten MOEA/D-Algorithmus, bezeichnet als TensorMOEA/D. In diesem Algorithmus wird die Umweltselektion in zwei Hauptphasen unterteilt: Vergleich und Populationsaktualisierung sowie Elite-Loesungsauswahl. Diese beiden Phasen werden hauptsaechlich durch zwei Anwendungen der vmap-Operation tensorisiert. Der detaillierte Prozess ist in Abb. 3 dargestellt.
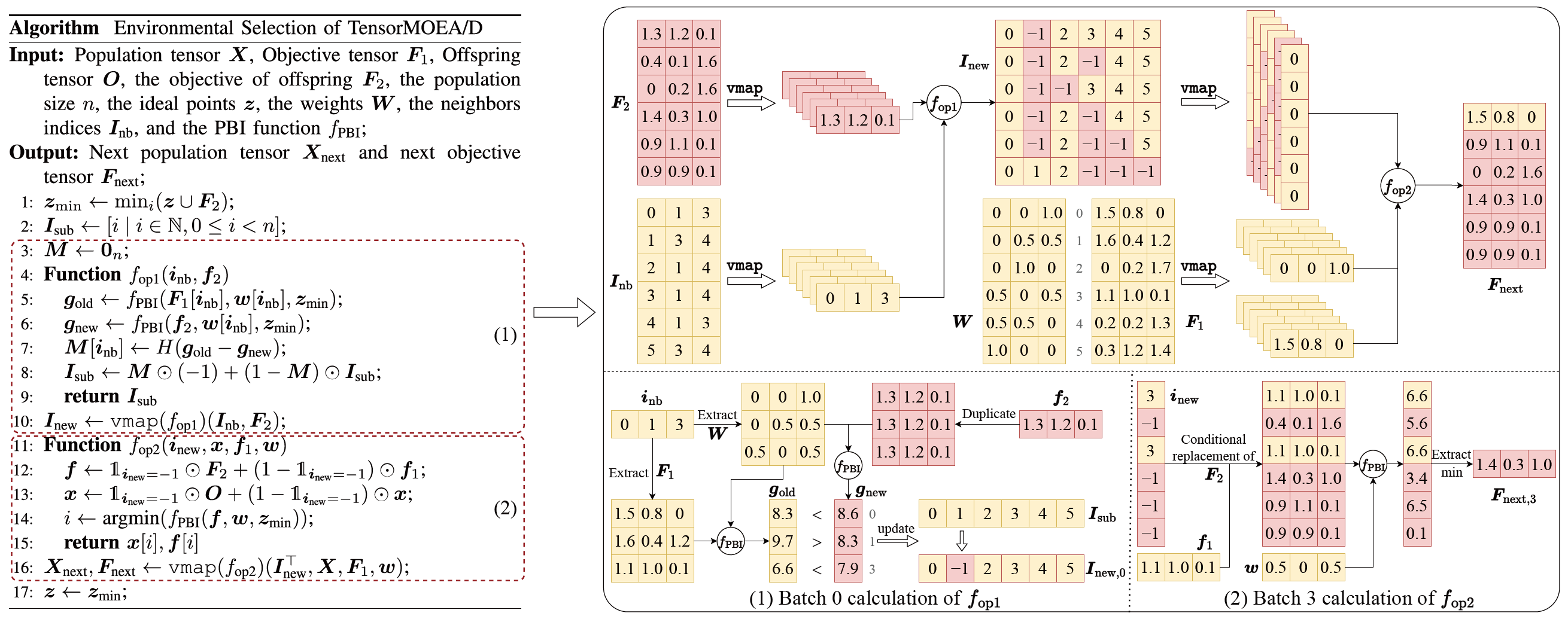
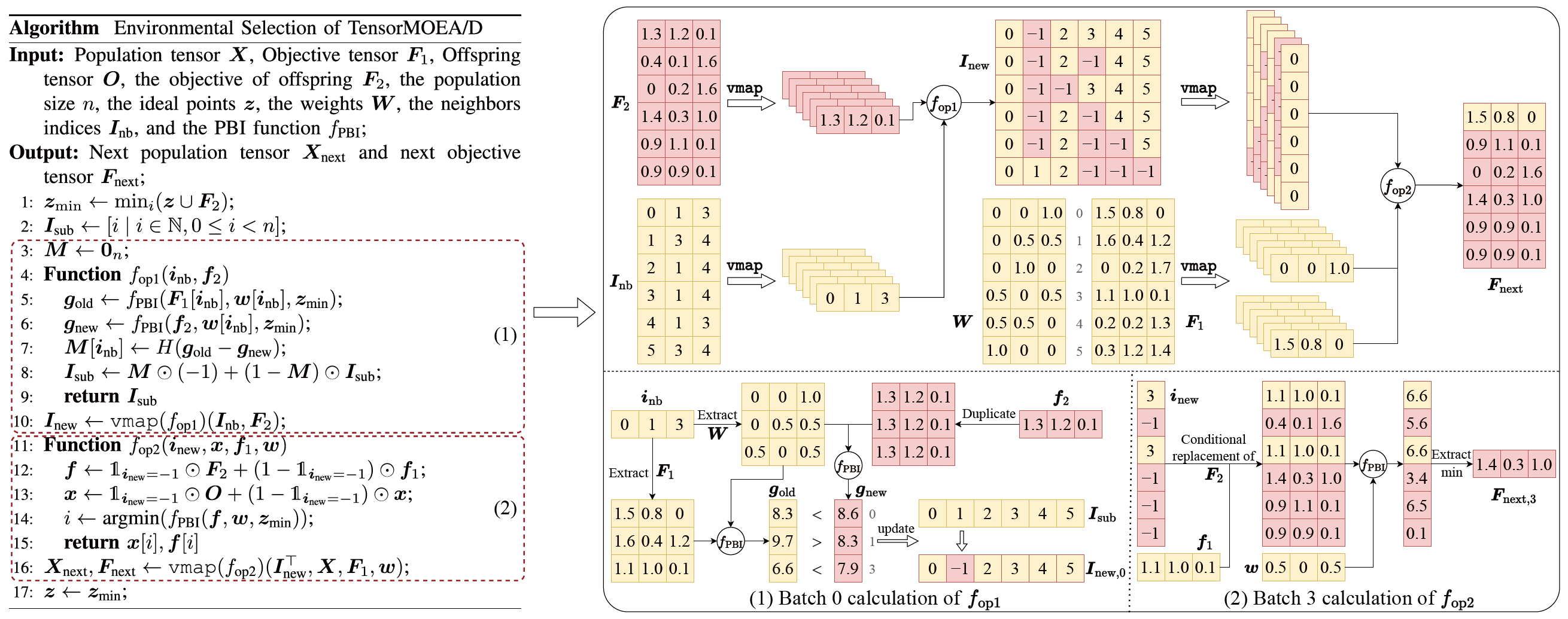
Abb.3: Ueberblick ueber die Umweltselektion im TensorMOEA/D-Algorithmus. Links: Pseudocode des Algorithmus. Rechts: Tensor-Datenfluss von Modul (1) und Modul (2). Der obere Teil der rechten Abb. zeigt den gesamten Tensor-Datenfluss fuer die Module (1) und (2), waehrend der untere Teil den Batch-Berechnungs-Tensor-Datenfluss zeigt, mit Modul (1) links und Modul (2) rechts.
Um ein umfassenderes Verstaendnis des Wertes der Tensorisierung in EMO-Algorithmen zu gewinnen, laesst sich dies aus drei Perspektiven zusammenfassen. Erstens ermoeglicht die Tensorisierung eine direkte Transformation von mathematischen Formulierungen zu effizientem Code und verringert die Kluft zwischen Algorithmus-Design und Implementierung. Beispielsweise zeigt Abb. 4, wie das tensorisierte nicht-dominierte Sortierverfahren direkt von Pseudocode in Python-Code uebersetzt werden kann. Zweitens vereinfacht die Tensorisierung die Codestruktur erheblich, indem Operationen auf Populationsebene in einer einzigen Tensordarstellung vereinheitlicht werden. Dies reduziert die Abhaengigkeit von Schleifen und bedingten Anweisungen und verbessert dadurch die Lesbarkeit und Wartbarkeit des Codes. Drittens verbessert die Tensorisierung die Reproduzierbarkeit von Algorithmen. Ihre strukturierte Darstellung erleichtert vergleichende Tests und die konsistente Reproduktion von Ergebnissen.

Abb.4: Die nahtlose Transformation des tensorisierten nicht-dominierten Sortierens von Pseudocode (links) zu Python-Code (rechts).
Leistungsdemonstration
Um die Leistung GPU-beschleunigter mehrkriterieller Optimierungsalgorithmen zu bewerten, fuehrte das EvoX-Team systematisch drei Kategorien von Experimenten durch, die sich auf rechnerische Beschleunigung, numerische Optimierungsleistung und Wirksamkeit bei mehrkriteriellen Robotersteuerungsaufgaben konzentrierten.
Rechnerische Beschleunigungsleistung:
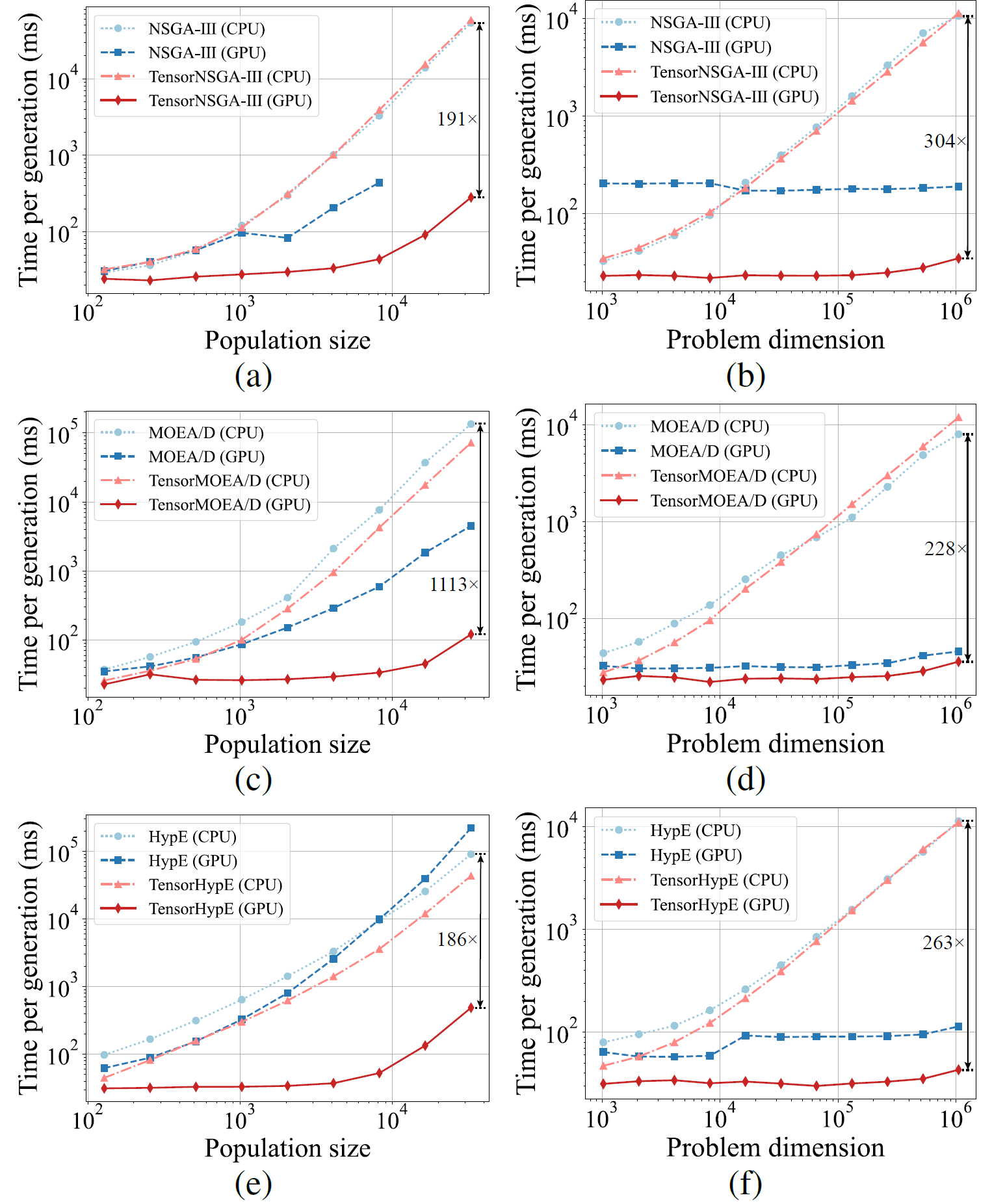
Abb.5: Vergleichende Beschleunigungsleistung von NSGA-III, MOEA/D und HypE mit ihren tensorisierten Gegenstuecken auf CPU- und GPU-Plattformen bei variierenden Populationsgroessen und Problemdimensionen.
Experimentelle Ergebnisse zeigen, dass TensorNSGA-III, TensorMOEA/D und TensorHypE auf GPUs deutlich hoehere Ausfuehrungsgeschwindigkeiten erreichen als ihre nicht-tensorisierten CPU-basierten Gegenstuecke. Mit zunehmender Populationsgroesse und Problemdimensionalitaet erreicht die maximal beobachtete Beschleunigung bis zu 1113x. Die tensorisierten Algorithmen zeigen ausgezeichnete Skalierbarkeit und Stabilitaet bei der Bewaeltigung grossskaliger Rechenaufgaben — ihre Laufzeit steigt nur geringfuegig, waehrend sie durchgehend hohe Leistung beibehalten. Diese Ergebnisse unterstreichen die erheblichen Vorteile der Tensorisierung fuer die GPU-Beschleunigung in der mehrkriteriellen Optimierung.
Leistung auf der LSMOP-Testsuite:
Tabelle II: Statistische Ergebnisse (Mittelwert und Standardabweichung) des IGD und der Laufzeit (s) fuer nicht-tensorisierte und tensorisierte EMO-Algorithmen in LSMOP1—LSMOP9. Alle Experimente wurden auf einer RTX 4090 GPU durchgefuehrt und die besten Ergebnisse sind hervorgehoben.
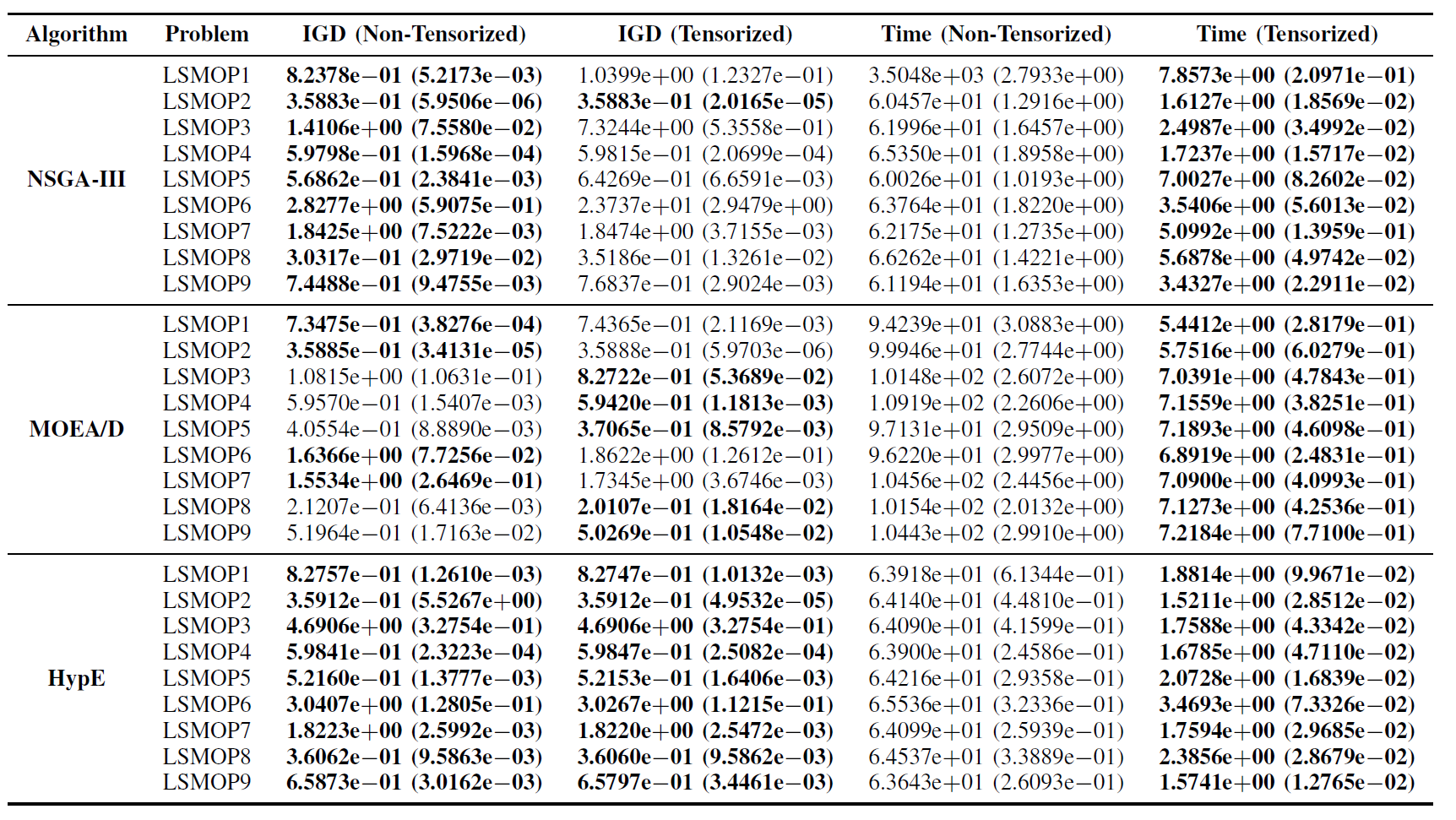
Experimentelle Ergebnisse zeigen, dass die GPU-beschleunigten EMO-Algorithmen auf Basis tensorisierter Darstellungen die Recheneffizienz erheblich verbessern und dabei die Optimierungsgenauigkeit ihrer urspruenglichen Gegenstuecke beibehalten und in einigen Faellen sogar uebertreffen.
Mehrkriterielle Robotersteuerungsaufgaben:
Um die praktische Leistung GPU-beschleunigter EMO-Algorithmen umfassend zu bewerten, entwickelte das Team eine Benchmark-Suite namens MoRobtrol fuer mehrkriterielle Robotersteuerung. Die in dieser Suite enthaltenen Aufgaben sind in Tabelle III aufgefuehrt.
Tabelle III: Ueberblick ueber mehrkriterielle Robotersteuerungsprobleme in der vorgeschlagenen MoRobtrol-Benchmark-Testsuite
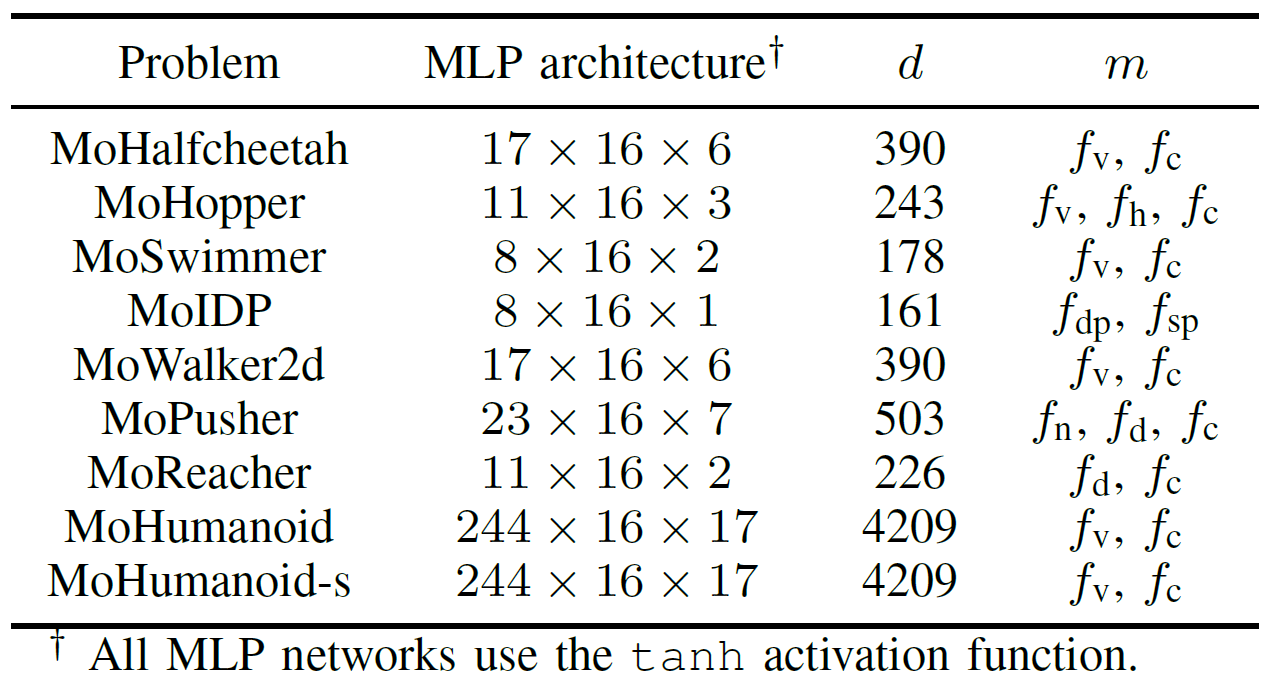
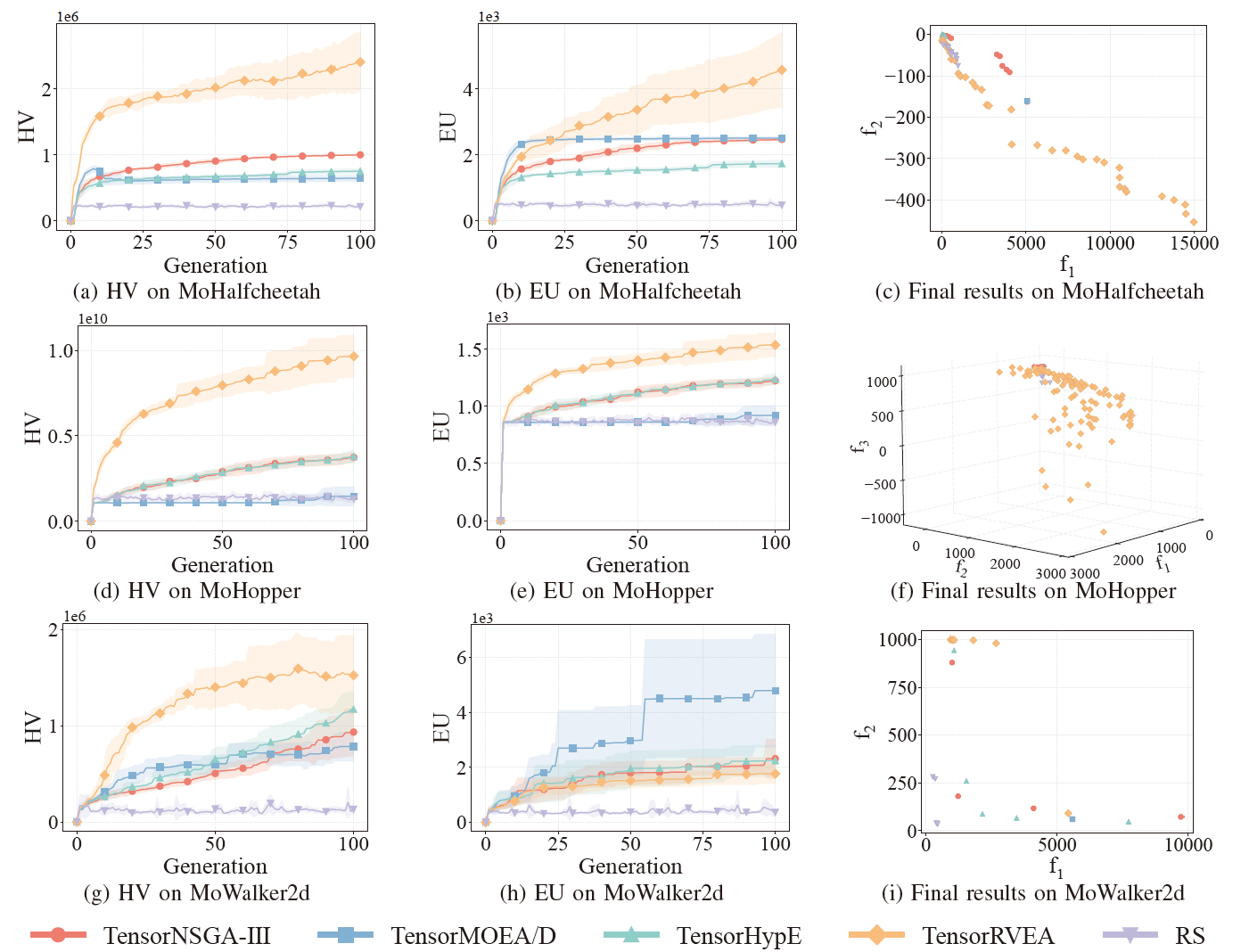
Abb.6: Vergleichende Leistung (HV, EU und Visualisierung der Endergebnisse) von TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA und Zufallssuche (RS) bei verschiedenen Problemen: MoHalfcheetah (390D), MoHopper (243D) und MoWalker2d (390D). Hinweis: Hoehere Werte bei allen Metriken zeigen bessere Leistung an.
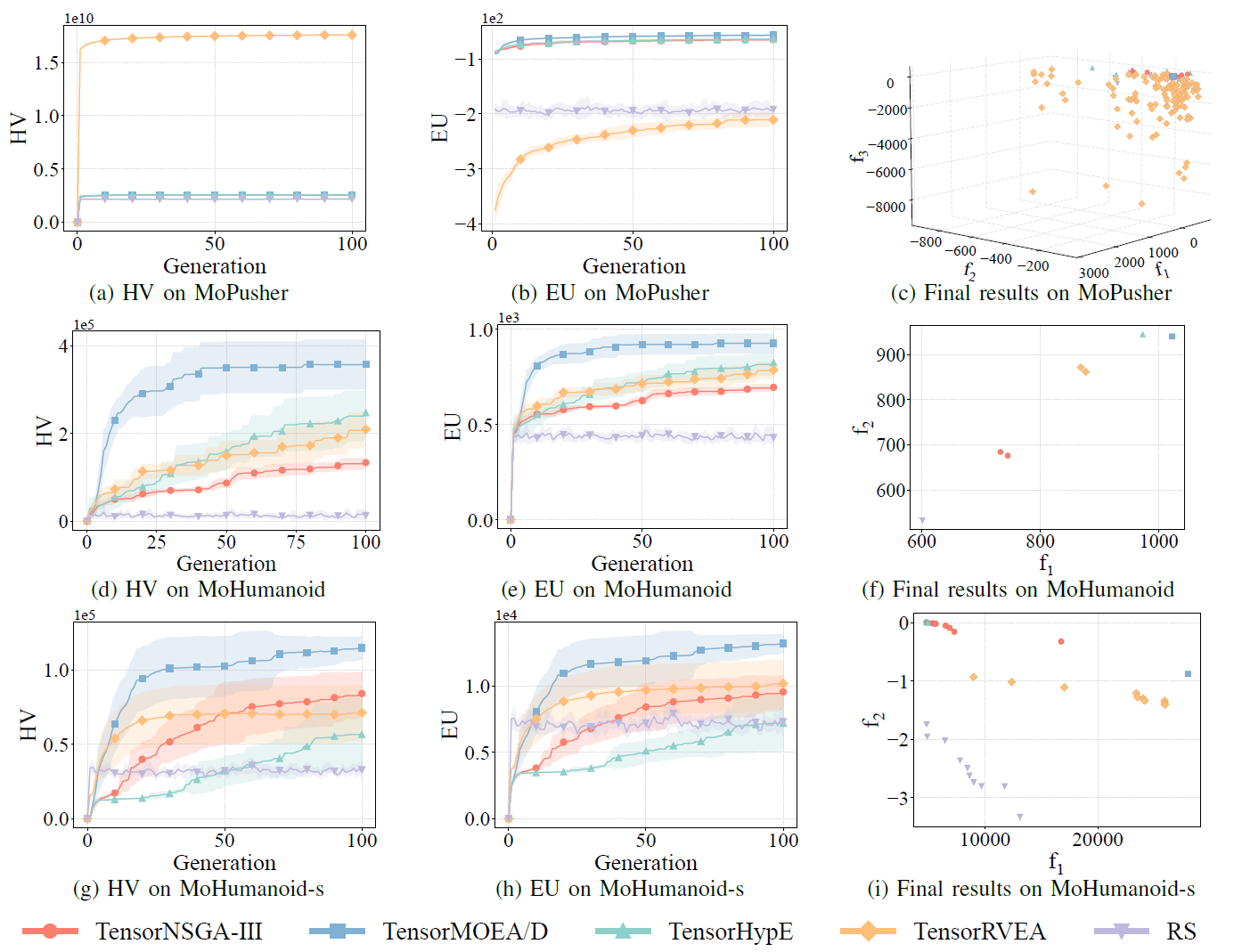
Abb.7: Vergleichende Leistung (HV, EU und Visualisierung der Endergebnisse) von TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA und Zufallssuche (RS) bei verschiedenen Problemen: MoPusher (503D), MoHumanoid (4209D) und MoHumanoid-s (4209D). Hinweis: Hoehere Werte bei allen Metriken zeigen bessere Leistung an.
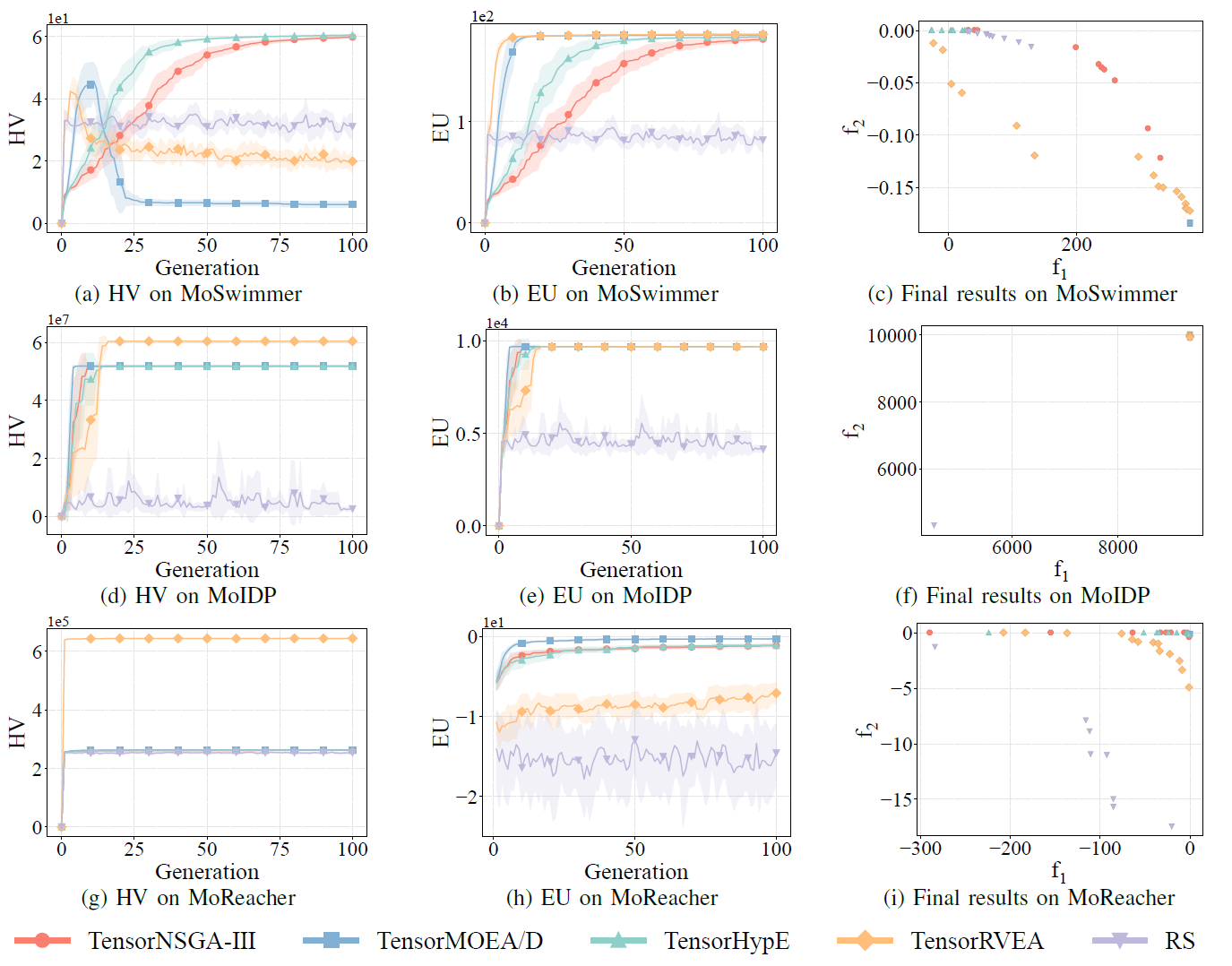
Abb.8: Vergleichende Leistung (HV, EU und Visualisierung der Endergebnisse) von TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA und Zufallssuche (RS) bei verschiedenen Problemen: MoSwimmer (178D), MoIDP (161D) und MoReacher (226D). Hinweis: Hoehere Werte bei allen Metriken zeigen bessere Leistung an.
Die Experimente verglichen die Leistung von TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA und Zufallssuche (RS) innerhalb des MoRobtrol-Benchmarks. Die Ergebnisse zeigen, dass TensorRVEA die beste Gesamtleistung erzielte, die hoechsten HV-Werte erreichte und gute Loesungsdiversitaet ueber mehrere Umgebungen hinweg demonstrierte. TensorMOEA/D zeigte starke Anpassungsfaehigkeit bei grossskaligen Aufgaben und zeichnete sich besonders durch Praeferenzkonsistenz der Loesungen aus. TensorNSGA-III und TensorHypE zeigten aehnliche Leistung und waren bei mehreren Aufgaben wettbewerbsfaehig. Insgesamt zeigten tensorisierte zerlegungsbasierte Algorithmen ueberlegene Vorteile bei der Loesung grossskaliger und komplexer Probleme.
Fazit und zukuenftige Arbeiten Diese Studie schlaegt eine tensorisierte Darstellungsmethodik vor, um die Einschraenkungen traditioneller CPU-basierter EMO-Algorithmen hinsichtlich Recheneffizienz und Skalierbarkeit zu ueberwinden. Der Ansatz wurde auf mehrere repraesentative Algorithmen angewendet, darunter NSGA-III, MOEA/D und HypE, und erzielte signifikante Leistungsverbesserungen auf GPUs bei gleichzeitiger Beibehaltung der Loesungsqualitaet. Um die praktische Anwendbarkeit zu validieren, entwickelte das Team auch MoRobtrol, eine Benchmark-Suite fuer mehrkriterielle Robotersteuerung, die Robotersteuerungsaufgaben in Physiksimulationsumgebungen als mehrkriterielle Optimierungsprobleme formuliert. Die Ergebnisse demonstrieren das Potenzial tensorisierter Algorithmen in rechenintensiven Szenarien wie verkoerperter Intelligenz. Obwohl die Tensorisierungsmethode die algorithmische Effizienz erheblich verbessert hat, besteht noch Raum fuer weitere Verbesserungen. Zukuenftige Richtungen umfassen die Verbesserung von Kernoperatoren wie nicht-dominiertem Sortieren, das Design neuer tensorisierter Operationen fuer Multi-GPU-Systeme und die Integration von grossskaligen Daten und Deep-Learning-Techniken zur weiteren Leistungssteigerung bei grossskaligen Optimierungsproblemen.
Open-Source-Code / Community-Ressourcen
Paper:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
Upstream-Projekt (EvoX):
https://github.com/EMI-Group/evox
QQ-Gruppe: 297969717

EvoMO basiert auf dem EvoX-Framework. Wenn Sie mehr ueber EvoX erfahren moechten, lesen Sie gerne den offiziellen Artikel ueber EvoX 1.0, der auf unserem WeChat-Konto veroeffentlicht wurde.


