Conectando la optimización multiobjetivo evolutiva
y la aceleración GPU mediante tensorización
Zhenyu Liang,Hao Li,Naiwei Yu, Kebin Sun, and Ran Cheng, Senior Member, IEEE
Con el aumento continuo en la demanda de soluciones de optimización complejas en dominios como el diseño de ingeniería y la gestión energética, los algoritmos de optimización multiobjetivo evolutiva (EMO) han atraído una atención generalizada debido a sus robustas capacidades para resolver problemas multiobjetivo. Sin embargo, a medida que las tareas de optimización crecen en escala y complejidad, los algoritmos EMO tradicionales basados en CPU encuentran cuellos de botella significativos en el rendimiento.
Para abordar esta limitación, el equipo de EvoX propuso paralelizar los algoritmos EMO en GPUs mediante la metodología de tensorización. Aprovechando este método, han diseñado e implementado exitosamente varios algoritmos EMO acelerados por GPU. Además, el equipo desarrolló “MoRobtrol”, una suite de benchmarks para control robótico multiobjetivo construida sobre el motor de física Brax, destinada a evaluar sistemáticamente el rendimiento de los algoritmos EMO acelerados por GPU.
Basándose en estos avances de investigación, el equipo de EvoX ha lanzado EvoMO, una biblioteca de algoritmos EMO acelerados por GPU de alto rendimiento. El código fuente correspondiente está disponible públicamente en GitHub: https://github.com/EMl-Group/evomo
Metodología de tensorización
En el campo de la optimización computacional, un tensor se refiere a una estructura de datos de arreglo multidimensional capaz de representar escalares, vectores, matrices y datos de orden superior. La tensorización es el proceso de convertir las estructuras de datos y operaciones dentro de un algoritmo a forma tensorial, permitiendo que el algoritmo aproveche completamente las capacidades de computación paralela de las GPUs.
En los algoritmos EMO, todas las estructuras de datos clave pueden expresarse en formato tensorizado. Los individuos en una población pueden representarse mediante un tensor de solución X, donde cada vector fila corresponde a un individuo. Los valores de la función objetivo forman un tensor objetivo F. Además, las estructuras de datos auxiliares como los vectores de referencia y los vectores de peso pueden expresarse como tensores R y W, respectivamente. Esta representación tensorial unificada permite operaciones a nivel de población en el nivel de representación, sentando una base sólida para la computación paralela a gran escala.
La tensorización de las operaciones de los algoritmos EMO es crucial para mejorar la eficiencia computacional y puede dividirse en dos capas: operaciones tensoriales básicas y tensorización del flujo de control. Las operaciones tensoriales básicas constituyen el núcleo de la implementación tensorizada de los algoritmos EMO, como se detalla en la Tabla I.
Tabla I: Operaciones tensoriales básicas

La tensorización del flujo de control reemplaza la lógica tradicional de bucles y condicionales con operaciones tensoriales paralelizables. Por ejemplo, los bucles for/while pueden transformarse en operaciones por lotes usando mecanismos de broadcasting o funciones de orden superior como vmap. De manera similar, los condicionales if-else pueden reemplazarse por técnicas de enmascaramiento, donde las condiciones lógicas se codifican como tensores booleanos, permitiendo el cambio flexible entre diferentes rutas de computación.
En comparación con las implementaciones tradicionales de algoritmos EMO, el enfoque de tensorización ofrece ventajas significativas. Primero, proporciona mayor flexibilidad, manejando naturalmente datos multidimensionales, mientras que los métodos convencionales a menudo están restringidos a operaciones de matrices bidimensionales. Segundo, la tensorización mejora significativamente la eficiencia computacional a través de la ejecución paralela, evitando la sobrecarga asociada con bucles explícitos y ramas condicionales. Por último, simplifica la estructura del código, resultando en programas más concisos y mantenibles.
Como se ilustra en la Fig. 1, por ejemplo, la implementación tradicional de la verificación de dominancia de Pareto depende de bucles anidados para realizar comparaciones elemento por elemento. En contraste, la versión tensorizada logra la misma funcionalidad a través de operaciones de broadcasting y enmascaramiento, permitiendo la evaluación paralela. Esto no solo reduce la complejidad del código sino que también mejora dramáticamente el rendimiento en tiempo de ejecución.

Fig.1: Comparación entre implementaciones convencionales y basadas en tensores de la detección de dominancia de Pareto.
Desde una perspectiva más profunda, la tensorización es adecuada para la aceleración GPU porque las GPUs poseen una gran cantidad de núcleos paralelos, y su arquitectura de instrucción única múltiples hilos (SIMT) se alinea naturalmente con las computaciones tensoriales, destacando particularmente en operaciones matriciales. Hardware dedicado como los Tensor Cores de NVIDIA mejora aún más el rendimiento de las operaciones tensoriales. En general, los algoritmos que exhiben alto paralelismo, contienen tareas computacionales independientes y tienen ramificación condicional mínima son más susceptibles a la tensorización. Para algoritmos como MOEA/D, que involucran dependencias secuenciales, la estructura inherente plantea desafíos para la tensorización directa. Sin embargo, a través de la refactorización estructural y el desacoplamiento de computaciones críticas, aún es posible lograr una aceleración paralela efectiva.
Ejemplo de aplicación de tensorización de algoritmos
Basándose en la metodología de representación tensorizada, el equipo de EvoX ha diseñado e implementado versiones tensorizadas de tres algoritmos EMO clásicos: el basado en dominancia NSGA-III, el basado en descomposición MOEA/D y el basado en indicadores HypE. La siguiente sección proporciona una explicación detallada usando MOEA/D como ejemplo. Las implementaciones tensorizadas de NSGA-III y HypE se pueden encontrar en el artículo referenciado.
Como se ilustra en la Fig. 2, el MOEA/D tradicional descompone un problema multiobjetivo en múltiples subproblemas, cada uno de los cuales se optimiza independientemente. El algoritmo comprende cuatro pasos centrales: cruce y mutación, evaluación de aptitud, actualización del punto ideal y actualización del vecindario. Estos pasos se ejecutan secuencialmente para cada individuo dentro de un solo bucle. Este procesamiento secuencial conduce a una sobrecarga computacional sustancial al tratar con poblaciones grandes, ya que cada individuo debe completar todos los pasos en orden, limitando los beneficios potenciales de la aceleración GPU. En particular, la actualización del vecindario depende de interacciones entre individuos, lo que complica aún más la paralelización.

Fig.2: Pseudocódigo de MOEA/D
Para abordar el problema de las dependencias secuenciales en el MOEA/D tradicional, el equipo introdujo un método de representación tensorizada dentro del bucle interno de la selección ambiental. Al desacoplar el cruce y mutación, la evaluación de aptitud, la actualización del punto ideal y la actualización del vecindario, estos componentes se tratan como operaciones independientes. Esto permite el procesamiento paralelo de todos los individuos, llevando a la construcción de un algoritmo MOEA/D tensorizado, denominado TensorMOEA/D. En este algoritmo, la selección ambiental se divide en dos etapas principales: comparación y actualización de población, y selección de soluciones élite. Estas dos etapas se tensorizan principalmente a través de dos aplicaciones de la operación vmap. El proceso detallado se ilustra en la Fig. 3.
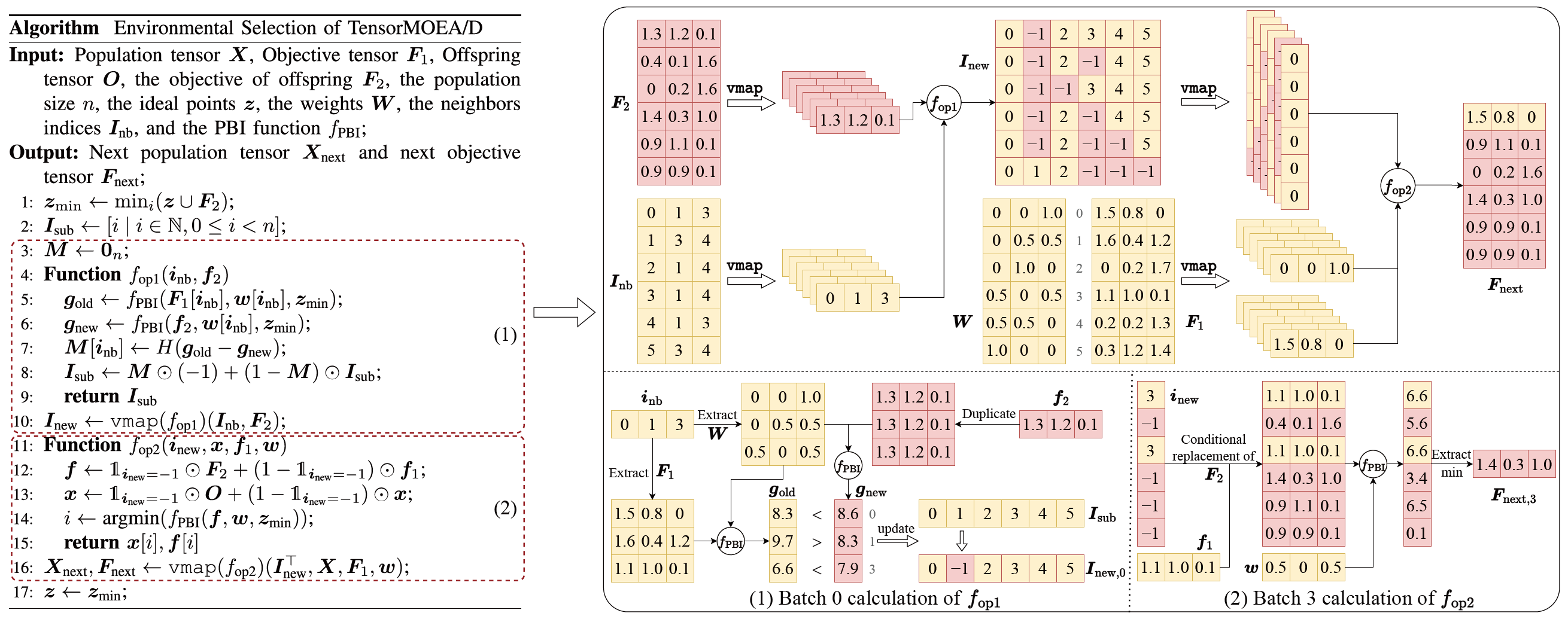
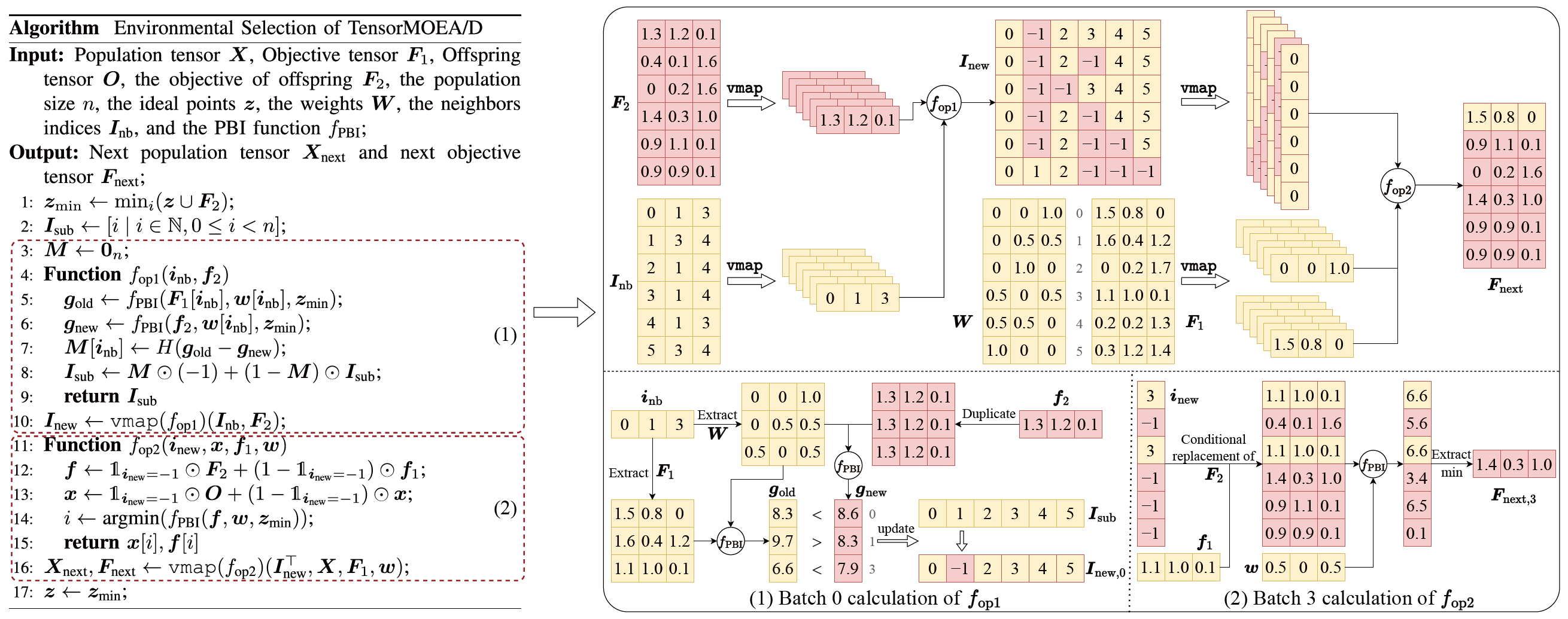
Fig.3: Visión general de la selección ambiental en el algoritmo TensorMOEA/D. Izquierda: Pseudocódigo del algoritmo. Derecha: Flujo de datos tensorial del módulo (1) y módulo (2). La parte superior de la Fig. derecha muestra el flujo de datos tensorial general para los módulos (1) y (2), mientras que la parte inferior presenta el flujo de datos tensorial de cálculo por lotes, con el módulo (1) a la izquierda y el módulo (2) a la derecha.
Para obtener una comprensión más completa del valor de la tensorización en los algoritmos EMO, se puede resumir desde tres perspectivas. Primero, la tensorización permite una transformación directa de formulaciones matemáticas a código eficiente, reduciendo la brecha entre el diseño del algoritmo y la implementación. Por ejemplo, la Fig. 4 ilustra cómo el procedimiento de ordenamiento no dominado tensorizado puede traducirse directamente de pseudocódigo a código Python. Segundo, la tensorización simplifica significativamente la estructura del código al unificar las operaciones a nivel de población en una sola representación tensorial. Esto reduce la dependencia de bucles y sentencias condicionales, mejorando así la legibilidad y mantenibilidad del código. Tercero, la tensorización mejora la reproducibilidad de los algoritmos. Su representación estructurada facilita las pruebas comparativas y la reproducción consistente de resultados.

Fig.4: La transformación fluida del ordenamiento no dominado tensorizado de pseudocódigo (izquierda) a código Python (derecha).
Demostración de rendimiento
Para evaluar el rendimiento de los algoritmos de optimización multiobjetivo acelerados por GPU, el equipo de EvoX realizó sistemáticamente tres categorías de experimentos, enfocándose en la aceleración computacional, el rendimiento de optimización numérica y la efectividad en tareas de control robótico multiobjetivo.
Rendimiento de aceleración computacional:
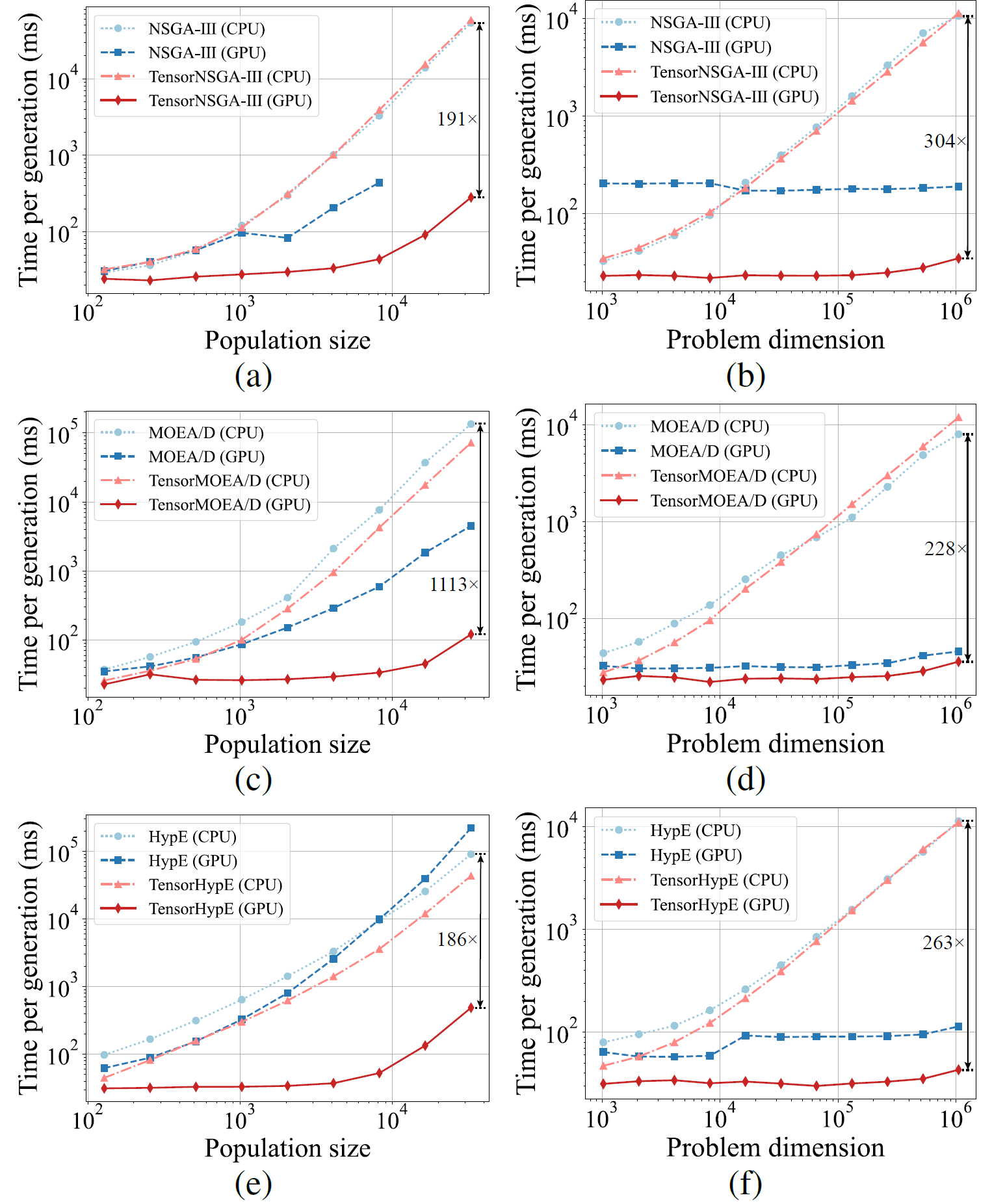
Fig.5: Rendimiento comparativo de aceleración de NSGA-III, MOEA/D y HypE con sus contrapartes tensorizadas en plataformas CPU y GPU con diferentes tamaños de población y dimensiones del problema.
Los resultados experimentales muestran que TensorNSGA-III, TensorMOEA/D y TensorHypE logran velocidades de ejecución significativamente mayores en GPUs en comparación con sus contrapartes no tensorizadas basadas en CPU. A medida que aumentan el tamaño de la población y la dimensionalidad del problema, la aceleración máxima observada alcanza hasta 1113x. Los algoritmos tensorizados demuestran excelente escalabilidad y estabilidad al manejar tareas computacionales a gran escala—su tiempo de ejecución aumenta solo marginalmente, mientras mantienen un rendimiento consistentemente alto. Estos hallazgos destacan las ventajas sustanciales de la tensorización para la aceleración GPU en optimización multiobjetivo.
Rendimiento en la suite de pruebas LSMOP:
Tabla II: Resultados estadísticos (media y desviación estándar) del IGD y tiempo de ejecución (s) para algoritmos EMO no tensorizados y tensorizados en LSMOP1—LSMOP9. Todos los experimentos se realizaron en una GPU RTX 4090 y los mejores resultados están resaltados.
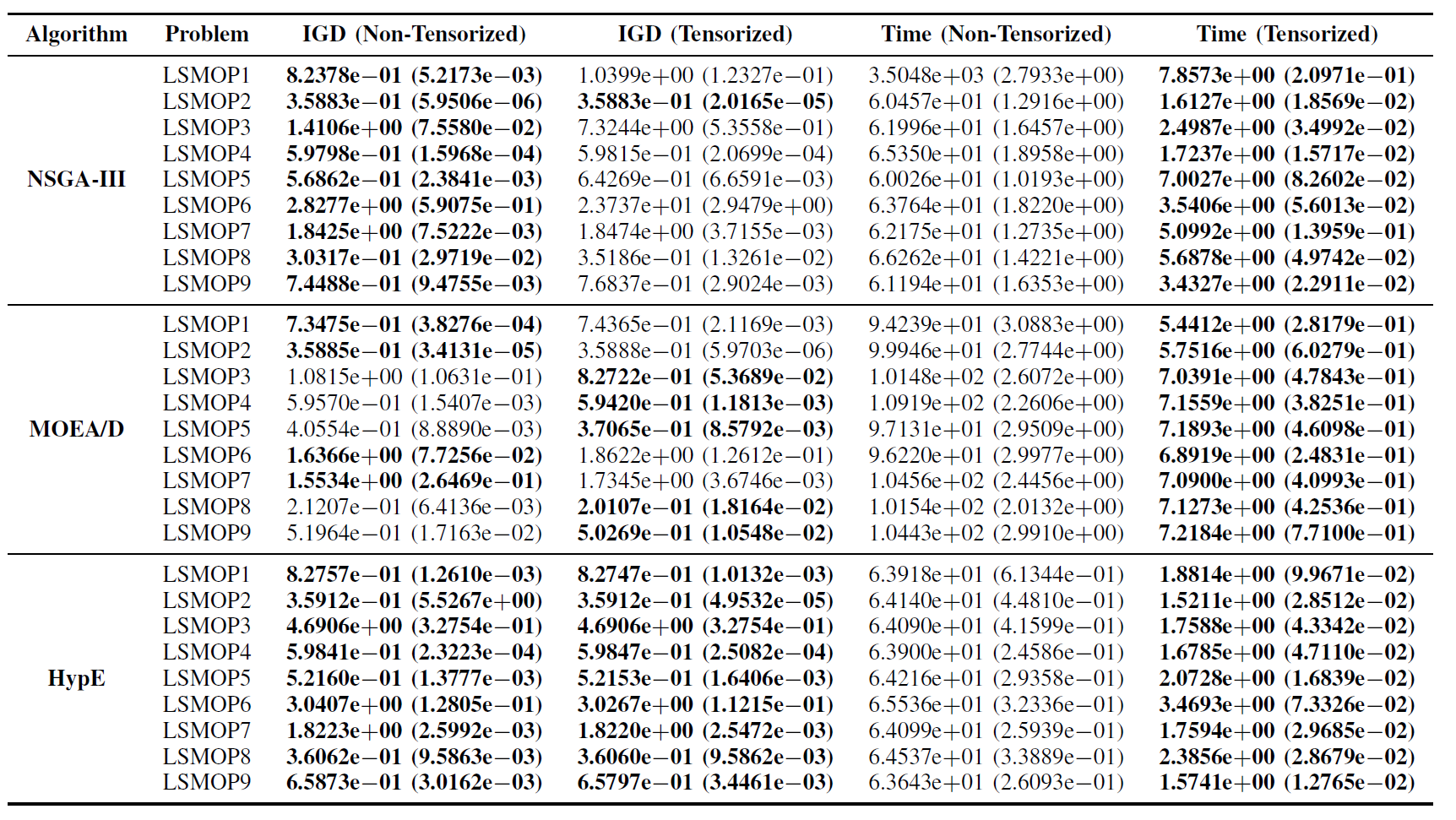
Los resultados experimentales indican que los algoritmos EMO acelerados por GPU basados en representaciones tensorizadas mejoran significativamente la eficiencia computacional mientras mantienen, y en algunos casos incluso superan, la precisión de optimización de sus contrapartes originales.
Tareas de control robótico multiobjetivo:
Para evaluar exhaustivamente el rendimiento práctico de los algoritmos EMO acelerados por GPU, el equipo desarrolló una suite de benchmarks llamada MoRobtrol para control robótico multiobjetivo. Las tareas incluidas en esta suite se enumeran en la Tabla III.
Tabla III: Resumen de los problemas de control robótico multiobjetivo en la suite de benchmarks MoRobtrol propuesta
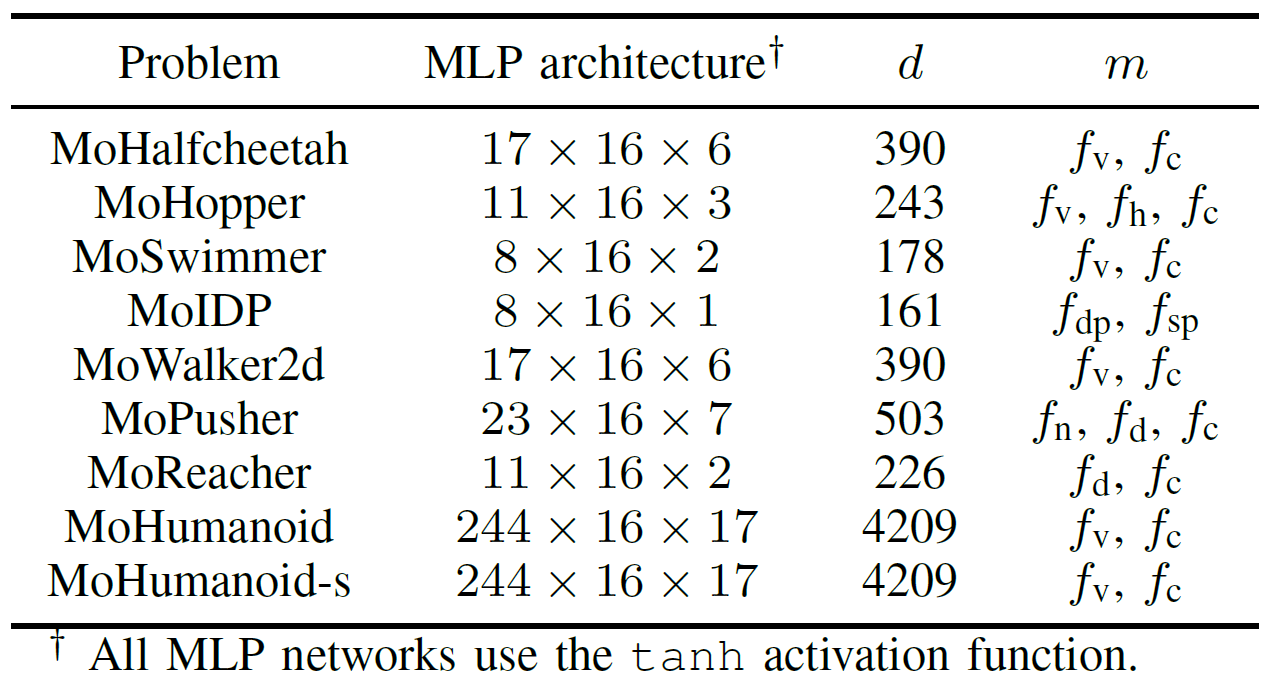
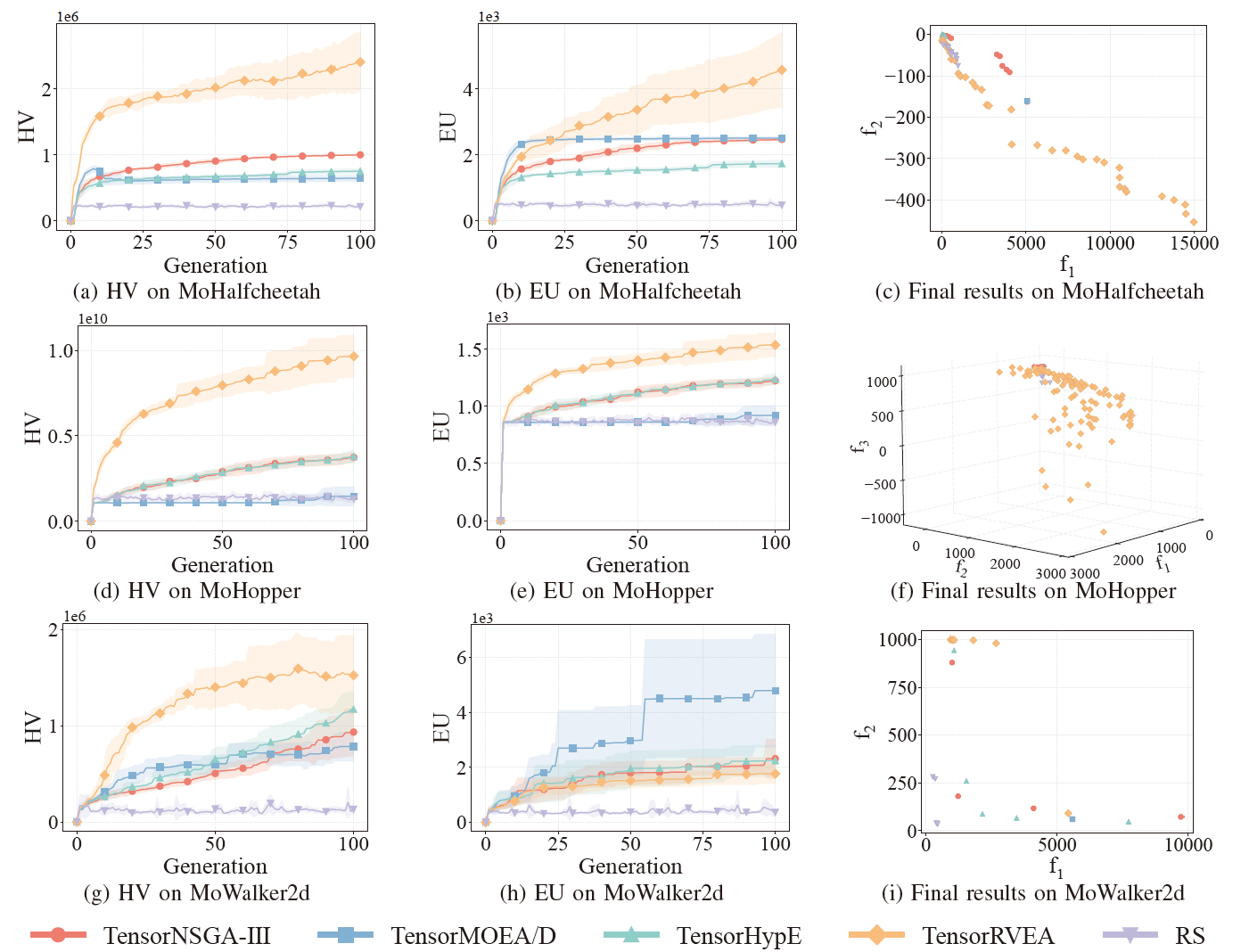
Fig.6: Rendimiento comparativo (HV, EU y visualización de resultados finales) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA y búsqueda aleatoria (RS) en diferentes problemas: MoHalfcheetah (390D), MoHopper (243D) y MoWalker2d (390D). Nota: Valores más altos para todas las métricas indican mejor rendimiento.
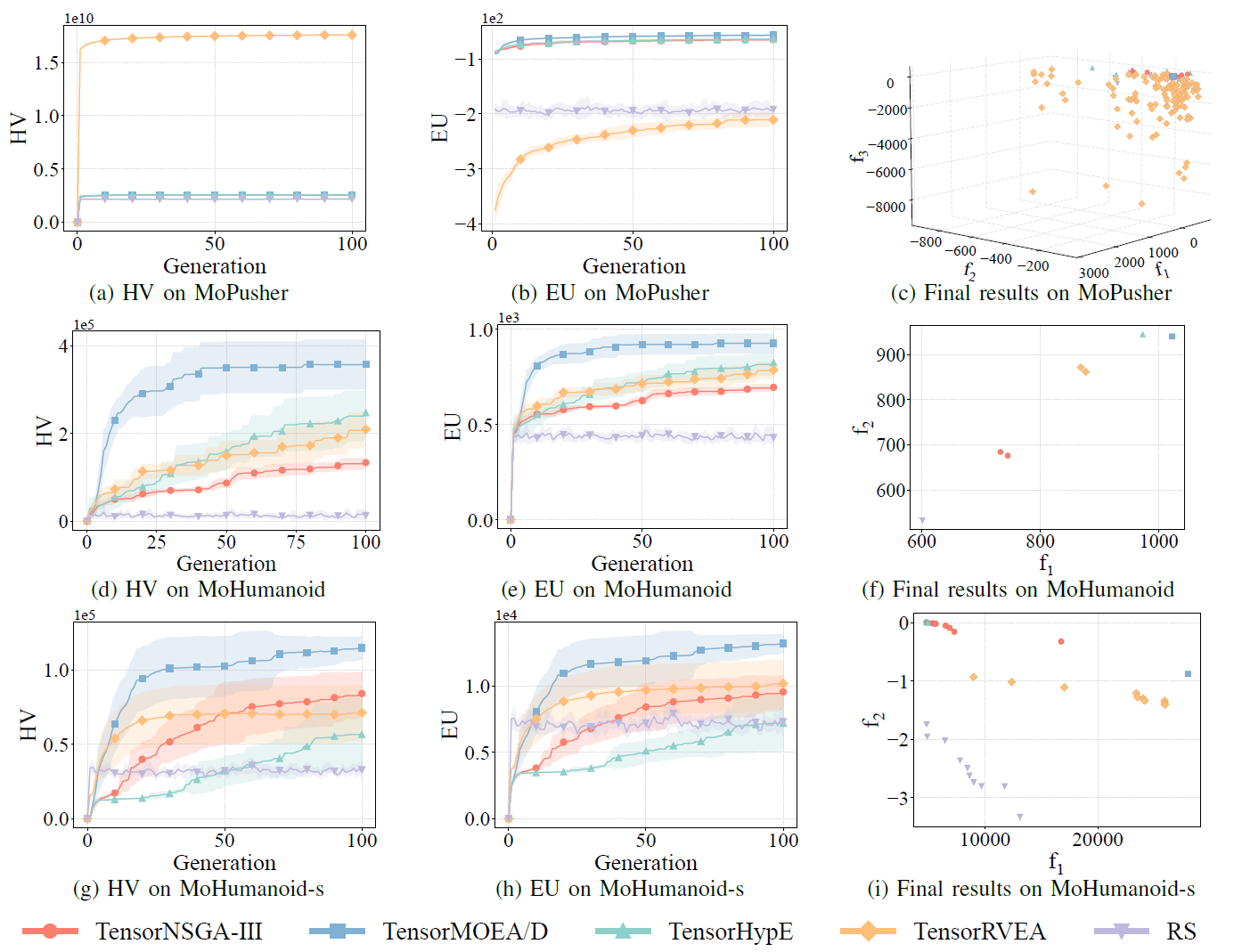
Fig.7: Rendimiento comparativo (HV, EU y visualización de resultados finales) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA y búsqueda aleatoria (RS) en diferentes problemas: MoPusher (503D), MoHumanoid (4209D) y MoHumanoid-s (4209D). Nota: Valores más altos para todas las métricas indican mejor rendimiento.
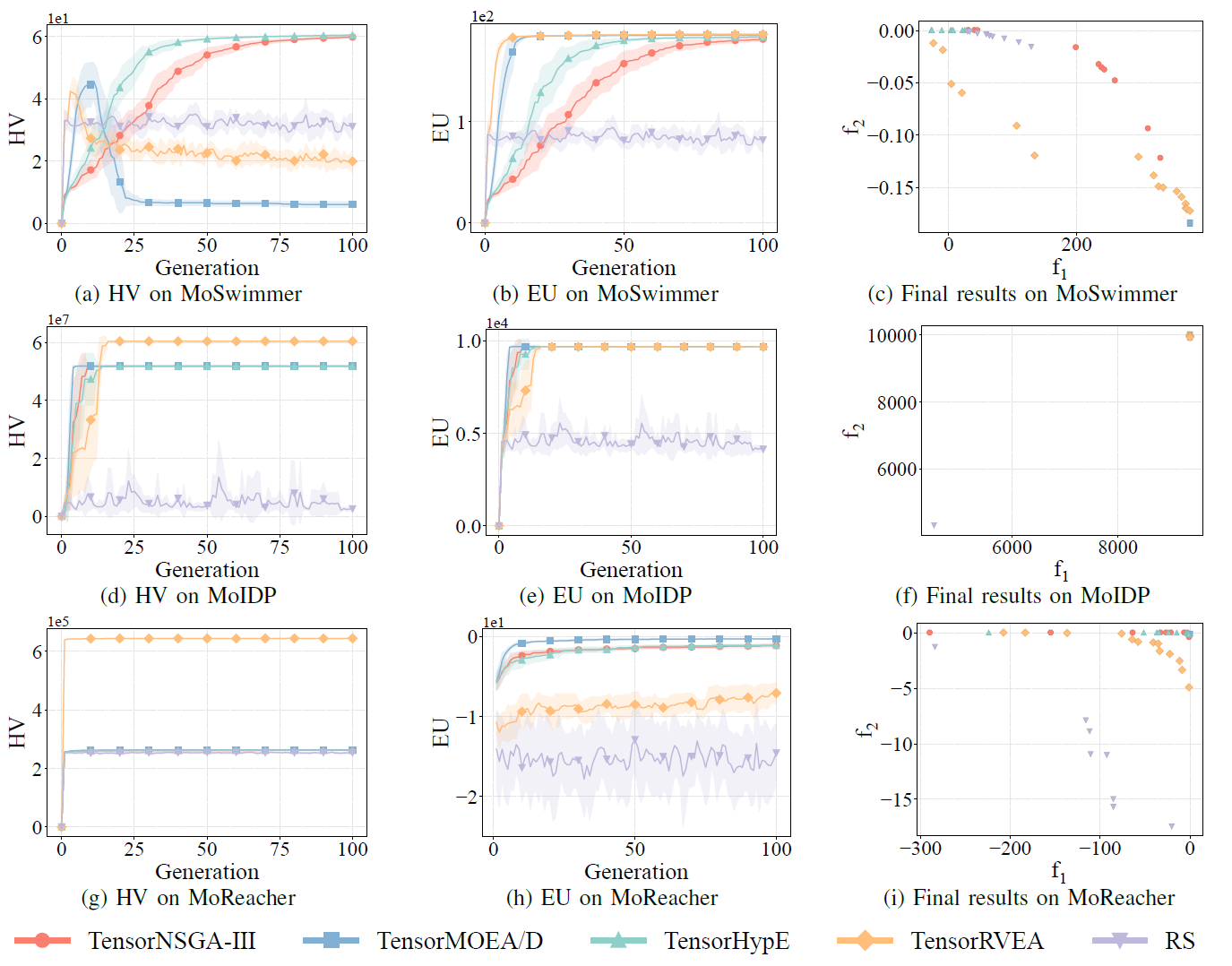
Fig.8: Rendimiento comparativo (HV, EU y visualización de resultados finales) de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA y búsqueda aleatoria (RS) en diferentes problemas: MoSwimmer (178D), MoIDP (161D) y MoReacher (226D). Nota: Valores más altos para todas las métricas indican mejor rendimiento.
Los experimentos compararon el rendimiento de TensorNSGA-III, TensorMOEA/D, TensorHypE, TensorRVEA y búsqueda aleatoria (RS) dentro del benchmark MoRobtrol. Los resultados muestran que TensorRVEA logró el mejor rendimiento general, obteniendo los valores HV más altos y demostrando buena diversidad de soluciones en múltiples entornos. TensorMOEA/D exhibió una fuerte adaptabilidad en tareas a gran escala, destacando particularmente en la consistencia de preferencias de las soluciones. TensorNSGA-III y TensorHypE mostraron un rendimiento similar y fueron competitivos en varias tareas. En general, los algoritmos tensorizados basados en descomposición demostraron ventajas superiores en la resolución de problemas a gran escala y complejos.
Conclusión y trabajo futuro Este estudio propone una metodología de representación tensorizada para abordar las limitaciones de los algoritmos EMO tradicionales basados en CPU en términos de eficiencia computacional y escalabilidad. El enfoque se ha aplicado a varios algoritmos representativos, incluyendo NSGA-III, MOEA/D y HypE, logrando mejoras significativas de rendimiento en GPUs mientras se mantiene la calidad de las soluciones. Para validar su aplicabilidad práctica, el equipo también desarrolló MoRobtrol, una suite de benchmarks de control robótico multiobjetivo que reformula las tareas de control robótico en entornos de simulación física como problemas de optimización multiobjetivo. Los resultados demuestran el potencial de los algoritmos tensorizados en escenarios computacionalmente intensivos como la inteligencia encarnada. Aunque el método de tensorización ha mejorado sustancialmente la eficiencia algorítmica, aún hay espacio para mejoras adicionales. Las direcciones futuras incluyen mejorar operadores centrales como el ordenamiento no dominado, diseñar nuevas operaciones tensorizadas para sistemas multi-GPU e integrar datos a gran escala y técnicas de aprendizaje profundo para mejorar aún más el rendimiento en problemas de optimización a gran escala.
Código abierto / Recursos comunitarios
Paper:
https://arxiv.org/abs/2503.20286
GitHub:
https://github.com/EMI-Group/evomo
Proyecto principal (EvoX):
https://github.com/EMI-Group/evox
Grupo QQ: 297969717

EvoMO está construido sobre el framework EvoX. Si están interesados en conocer más sobre EvoX, no duden en consultar el artículo oficial sobre EvoX 1.0 publicado en nuestra cuenta pública de WeChat para más detalles.


